Методические рекомендации и указания к решению задач к главе 1

Задачи на кинематику материальной точки предусматривают задание явной зависимости от времени одной из кинематических характеристик (). В этом случае остальные характеристики движения могут быть найдены путём дифференцирования или интегрирования величины. По известному закону движения можно найти уравнение траектории движения тела, определить среднюю скорость и ускорение, получить зависимость скорости и ускорения от времени движения. С другой стороны, если известны скорость или ускорение как функции времени и начальные условия (координаты и скорость в начальный момент времени), то можно найти закон движения.

Для решения задач такого типа необходимо знать правила дифференцирования и значения табличных интегралов.

Примеры решения задач

Пример 1.1. Радиус-вектор точки относительно начала координат изменяется со временем по закону , где α, β, ω – постоянные. Найти вектор скорости, вектор ускорения, а также их модули.

Решение

- вектор скорости

- модуль скорости

- вектор ускорения

- -модуль ускорения

Пример 1.2. Найти скорость и ускорение тела через t = 10с после начала движения, если х =Асоs ωt y = В sin ωt. А = 1м; В = 3м.

Решение

Скорость и ускорение в произвольный момент времени:

при t = 10с м/с;м/с²

Пример 1.3. Зависимость модуля скорости материальной точки от времени имеет вид υ(t) = α+βt² , где α, β – постоянные. При t = 0 тело находилось в начале координат, т.е. S = 0. Определите путь, пройденный точкой за время от t₁ =0 до

t₂ = τ.

Решение

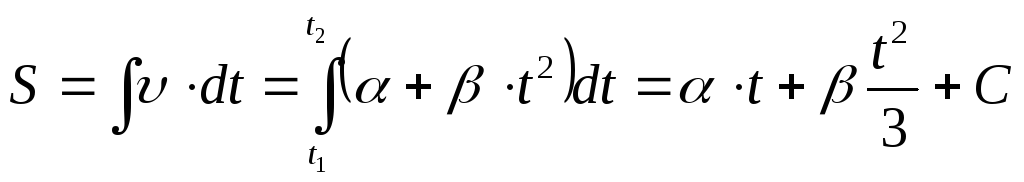
где С – постоянная интегрирования, которую определяем из начальных условий, т.е. при t =0 S₀ =0, получаем , получаем С = 0.

Т.о.

Пример 1.4. Найти уравнение траектории, если скорость материальной точки зависит от времени как . В момент t = 0 тело находилось в начале координат.

Указания: Для нахождения уравнения траектории в явном виде необходимо из параметрических уравнений движения исключить время и выразить одну координату материальной точки через другую х=f(у) или у=f(x).

Решение

Найдём зависимость радиус-вектора от времени

Из начальных условий следует, что .. Таким образом,

Исключив время, получаем уравнение траектории

представляющей собой параболу.

Пример 1.5. Движение точки по прямой задано уравнением х = 4t – 2t². Определить среднюю скорость в интервале времени от t₁ = 0 до t₂ = 1с.

Указания: При поступательном движении значение средней скорости и ускоренияопределяем по формуле:

Решение

м/с

Пример 1.6. Частица движется в положительном направлении оси так, что её скорость меняется по закону , где α- положительная постоянная. Имея в виду, что в момент t = 0 она находится в точке х = 0. Найти зависимость от времени скорости частицы.

Указание: постановка задачи может быть усложнена неявным заданием зависимости характеристик движения от времени Ф [φ(t)]. При этом необходимо выделить явную зависимость от времени, используя правила дифференцирования сложной функции

Решение

Скорость частицы зависит от её координаты, которая в свою очередь зависит от времени. Следовательно, скорость частицы зависит от времени. Следовательно, скорость частицы зависит от времени. Найдём производную от скорости по времени

Отсюда находим искомую величину

Так как при t = 0, x = 0 ( а значит и υ = 0), С = 0, получаем окончательно

Пример 1.7. Твёрдое тело вращается вокруг неподвижной оси по закону

, где α = 6 с^{-1 ;} β = 2 с^-3. Найти угловое ускорение в момент остановки тела.

Решение

Условие остановки , откуда находим время движения до остановки,

Т. к. , получим β в момент остановки

Пример 1.8. Материальная точка вращается по окружности радиуса R так, что угол поворота зависит от времени по закону , где α – постоянная. Найти зависимость от времени полного ускорения.

Решение

Полное ускорение в проекциях на касательную и нормаль в каждой точке траектории

Модуль полного ускорения определяем по теореме Пифагора:

где

R –радиус кривизны траектории

Рис.1.8

Пример 1.9. Материальная точка движется по окружности радиуса 4м. Зависимость пути от времени задана уравнением S=Ct³, где С = 0,02м/с³. Найти ускорение и его тангенциальную и нормальную составляющие в момент, когда скорость точки равна υ₁=6м/с.

Решение

Запишем зависимость скорости от времени:

(1)

Отсюда найдём время t₁, когда скорость равна υ₁:

(2)

Тангенциальную составляющую ускорения вычисляем по формуле , учитывая (1):

(3)

Подставив (2) в (3), имеем

(4)

Нормальную составляющую ускорения найдём, используя формулу

(5)

Подставив в (4) значения υ₁ и С, а в (5) υ₁ и R, получаем ответы:

а_τ =1,2 м/с² и а_n = 9 м/с².

Используя формулы (4) и (5) и теорему Пифагора, найдём ускорение

(6)

Подставив в (6) значения υ₁, С и R, получим а = 9,08 м/с²