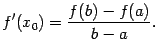- •1Система аксиом действительных чисел.
- •4 Открытое покрытие отрезка
- •Первое доказательство
- •Второе доказательство
- •5Предельная точка множества. Предел функции в точке
- •6Предел последовательности
- •7Свойства сходящихся последовательностей
- •8 Теоремы о предельном переходе в неравенствах.
- •9 Критерий коши сходимости последовательности
- •10 Свойства монотонных последовательностей
- •14 Св-ва пределов
- •21 Http://joxi.Ru/qmtgUhjKtja2asPky84
- •23 Непрерывность обратной функции
- •24Теорема (о разрывах монотонной функции)
- •Доказательство этой теоремы легко следует из теоремы о существовании предела монотонной функции.
- •30 Http://joxi.Ru/mm3gUv3jtjcwEaipblM
- •35 Http://joxi.Ru/19jGUhjKtjbaAdNjO7m
- •41 Введение в специальность – искать там
- •44 Http://joxi.Ru/6t_gUhjKtja7AdX473u
30 Http://joxi.Ru/mm3gUv3jtjcwEaipblM
31 Теорема 5.1 (Ферма)
Пусть
функция ![]() имеет
на множестве
имеет
на множестве ![]() точку
экстремума
точку
экстремума ![]() ,
причём множество
,
причём множество ![]() содержит
некоторую
содержит
некоторую ![]() -окрестность
-окрестность ![]() точки
точки ![]() .
Тогда либо
.
Тогда либо ![]() имеет
в точке
имеет
в точке ![]() производную,
равную 0, то есть
производную,
равную 0, то есть ![]() ,
либо производная в точке
,
либо производная в точке ![]() не
существует.
Доказательство теоремы
Ферма. Если производная в
точке экстремума не существует, то
утверждение теоремы верно. Предположим,
что производная
не
существует.
Доказательство теоремы
Ферма. Если производная в
точке экстремума не существует, то
утверждение теоремы верно. Предположим,
что производная ![]() существует.
Рассмотрим два случая.
существует.
Рассмотрим два случая.
Пусть
функция имеет в точке ![]() максимум.
Тогда
максимум.
Тогда![]() при
всех
при
всех![]() ,
поскольку
,
поскольку![]() .
Если взять
.
Если взять![]() ,
то
,
то![]() ,
и поэтому
,
и поэтому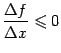 .
При вычислении производной мы переходим
к пределу при
.
При вычислении производной мы переходим
к пределу при![]() в
этом разностном отношении. При этом
знак нестрогого неравенства сохраняется,
когда мы берём предел справа:
в
этом разностном отношении. При этом
знак нестрогого неравенства сохраняется,
когда мы берём предел справа:
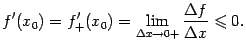
Аналогично,
при ![]() ,
,![]() ,
и поэтому
,
и поэтому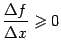 .
Отсюда, вычисляя предел слева, получаем:
.
Отсюда, вычисляя предел слева, получаем:
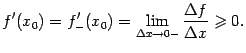
Итак,
выполняются два неравенства: ![]() и
и![]() ,
что возможно лишь при
,
что возможно лишь при![]() .
.
Пусть
теперь функция ![]() имеет
в точке
имеет
в точке![]() минимум.
Тогда
минимум.
Тогда![]() при
всех
при
всех![]() ,
поскольку
,
поскольку![]() .
Если взять
.
Если взять![]() ,
то
,
то![]() ,
и поэтому
,
и поэтому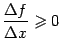 .
Переходя к пределу при
.
Переходя к пределу при![]() в
разностном отношении, получаем:
в
разностном отношении, получаем:
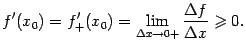
Аналогично,
при ![]() ,
,![]() ,
и поэтому
,
и поэтому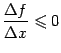 .
Вычисляя предел слева, получаем:
.
Вычисляя предел слева, получаем:
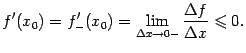
Из
неравенств ![]() и
и![]() получаем,
что
получаем,
что![]() .
.
32 Теорема 5.2 (Ролля)
Пусть
функция ![]() дифференцируема
на интервале
дифференцируема
на интервале ![]() ,
непрерывна в точках
,
непрерывна в точках ![]() и
и ![]() и
принимает в этих точках значение 0:
и
принимает в этих точках значение 0: ![]() .
Тогда найдётся хотя бы одна точка
.
Тогда найдётся хотя бы одна точка ![]() ,
в которой
,
в которой ![]() .
.
Доказательство теоремы
Ролля. Так как при наших
предположениях функция ![]() непрерывна
на отрезке
непрерывна
на отрезке![]() ,
то она принимает своё максимальное
значение
,
то она принимает своё максимальное
значение![]() и
минимальное значение
и
минимальное значение![]() в
некоторых точках
в
некоторых точках![]() и
и![]() этого
отрезка.
этого
отрезка.
Рассмотрим
два случая. Если ![]() ,
то наибольшее и наименьшее значения
функции совпадают, и, следовательно,
функция постоянна на отрезке
,
то наибольшее и наименьшее значения
функции совпадают, и, следовательно,
функция постоянна на отрезке![]() :
:![]() .
Значит,
.
Значит,![]() при
всех
при
всех![]() ,
и в качестве
,
и в качестве![]() в
этом случае можно взять любую
точку
в
этом случае можно взять любую
точку![]() интервала
интервала![]() .
.
Если
же ![]() ,
то либо
,
то либо![]() ,
либо
,
либо![]() отлично
от 0 и, следовательно, либо точка
отлично
от 0 и, следовательно, либо точка![]() ,
либо точка
,
либо точка![]() не
совпадает с концами отрезка
не
совпадает с концами отрезка![]() и
и![]() ,
то есть лежит внутри интервала
,
то есть лежит внутри интервала![]() .
Пусть, для определённости,
.
Пусть, для определённости,![]() --
внутренняя точка интервала. Тогда, по
теореме Ферма,
--
внутренняя точка интервала. Тогда, по
теореме Ферма,![]() ,
поскольку по предположению доказываемой
теоремы,
,
поскольку по предположению доказываемой
теоремы,![]() имеет
производную во всех точках интервала
имеет
производную во всех точках интервала![]() и,
следовательно, в точке
и,
следовательно, в точке![]() .
Итак, в этом случае точку
.
Итак, в этом случае точку![]() можно
взять в качестве искомой точки
можно
взять в качестве искомой точки![]() :
тогда
:
тогда![]() .
.
33Теорема 5.3 (Лагранжа)
Пусть
функция ![]() дифференцируема
на интервале
дифференцируема
на интервале![]() и
непрерывна в точках
и
непрерывна в точках![]() и
и![]() .
Тогда найдётся такая точка
.
Тогда найдётся такая точка![]() ,
что
,
что
|
|
(5.1) |
Доказательство теоремы
Лагранжа. Дадим сначала
геометрическую иллюстрацию теоремы.
Соединим конечные точки графика ![]() на
отрезке
на
отрезке ![]() хордой.
Конечные приращения
хордой.
Конечные приращения ![]() и
и ![]() --
это величины катетов треугольника,
гипотенузой которого служит проведённая
хорда.
--
это величины катетов треугольника,
гипотенузой которого служит проведённая
хорда.
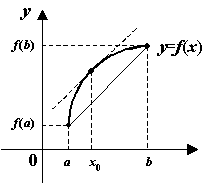
Рис.5.5.Касательная в некоторой точке параллельна хорде
Отношение
конечных приращений ![]() и
и ![]() --
это тангенс угла наклона хорды. Теорема
утверждает, что к графику дифференцируемой
функции можно провести в некоторой
точке
--
это тангенс угла наклона хорды. Теорема
утверждает, что к графику дифференцируемой
функции можно провести в некоторой
точке ![]() касательную,
которая будет параллельна хорде, то
есть угол наклона касательной
касательную,
которая будет параллельна хорде, то
есть угол наклона касательной ![]() (
( ![]() )
будет равен углу наклона хорды
)
будет равен углу наклона хорды ![]() (
( 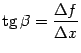 ).
Но наличие такой касательной геометрически
очевидно.
).
Но наличие такой касательной геометрически
очевидно.
Заметим,
что проведённая хорда, соединяющая
точки ![]() и
и ![]() --
это график линейной функции
--
это график линейной функции ![]() .
Поскольку угловой коэффициент этой
линейной функции равен, очевидно,
.
Поскольку угловой коэффициент этой
линейной функции равен, очевидно, 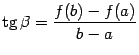 ,
то
,
то
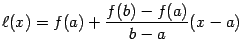
(мы
учли то, что график линейной функции
проходит через точку ![]() ).
).
Сведём
доказательство к применению теоремы
Ролля. Для этого введём вспомогательную
функцию ![]() ,
то есть
,
то есть
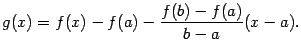
Заметим,
что ![]() и
и ![]() (по
построению функции
(по
построению функции ![]() ).
Так как линейная функция
).
Так как линейная функция ![]() дифференцируема
при всех
дифференцируема
при всех ![]() ,
то функция
,
то функция ![]() удовлетворяет,
тем самым, всем свойствам, перечисленным
в условии теоремы Ролля. Поэтому найдётся
такая точка
удовлетворяет,
тем самым, всем свойствам, перечисленным
в условии теоремы Ролля. Поэтому найдётся
такая точка ![]() ,
что
,
что ![]() .
.
Заметим теперь, что
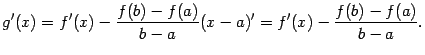
Значит,
равенство ![]() можно
переписать в виде
можно
переписать в виде
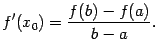
Таким образом, мы доказали формулу (5.1).
Теорема 5.4 (Коши)
Пусть
функции ![]() и
и![]() дифференцируемы
на интервале
дифференцируемы
на интервале![]() и
непрерывны при
и
непрерывны при![]() и
и![]() ,
причём
,
причём![]() при
всех
при
всех![]() .
Тогда в интервале
.
Тогда в интервале![]() найдётся
такая точка
найдётся
такая точка![]() ,
что
,
что
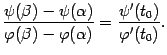
Доказательство.
Докажем сначала, что ![]() ,
то есть что дробь в левой части формулы
имеет смысл. Действительно, для этой
разности можно записать формулу конечных
приращений:
,
то есть что дробь в левой части формулы
имеет смысл. Действительно, для этой
разности можно записать формулу конечных
приращений:
![]()
при
некотором ![]() .
Но в правой части этой формулы оба
множителя отличны от нуля.
.
Но в правой части этой формулы оба
множителя отличны от нуля.
Для доказательства теоремы применим тот же приём, что при доказательстве теоремы Лагранжа: введём вспомогательную функцию
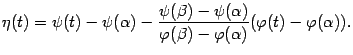
Функция ![]() ,
очевидно, является дифференцируемой
при всех
,
очевидно, является дифференцируемой
при всех![]() и
непрерывной в точках
и
непрерывной в точках![]() и
и![]() ,
поскольку этими свойствами обладают
функции
,
поскольку этими свойствами обладают
функции![]() и
и![]() .
Кроме того, очевидно, что при
.
Кроме того, очевидно, что при![]() получается
получается![]() .
Покажем, что и
.
Покажем, что и![]() :
:
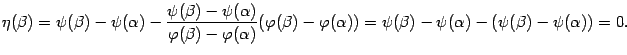
Значит,
функция ![]() удовлетворяет
на отрезке
удовлетворяет
на отрезке![]() условиям
теоремы Ролля. Поэтому существует такая
точка
условиям
теоремы Ролля. Поэтому существует такая
точка![]() ,
что
,
что![]() .
.
Вычислим
теперь производную функции ![]() :
:
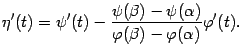
Получаем, что
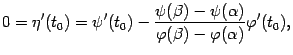
откуда получаем утверждение теоремы:
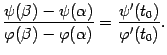
http://webmath.exponenta.ru/s/kiselev1/node52.htm
34ДАРБУ ТЕОРЕМА
если функция в каждой точке некоторого промежутка оси действительных чисел имеет конечную производную, то, принимая два каких-либо значения на этом промежутке, производная принимает на нем и любое промежуточное.
Пусть ![]() дифференцируема
на
дифференцируема
на ![]() .
Тогда
.
Тогда ![]()
|
Доказательство: |
|
|
|
Для
определенности считаем, что Рассмотрим
вспомогательную функцию
По
определению производной, При Аналогично
рассмотрим Функция Пусть
оно достигается в точке |