МУ ТМ_2015 / Кинематика (Живаго, Михайленко)
.pdf
Институт машиностроения и транспорта
Кафедра теоретической механики
КИНЕМАТИКА
Практикум
|
|
3 |
ω3 |
ε3 |
|
ε2 |
R2 r2 |
|
|
|
|
ω2 |
|
R3 |
|
|
|
1 |
|
|
r3 |
|
|
|
|
|
|
|
|
V 1 |
2 |
V M |
аМ |
аМп |
|
|
|
|
|||
х |
|
аτ |
3R4 |
ω |
|
|
М |
|
|
4 |
|
М
4 ε4
Новокузнецк
2012
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
“Сибирский государственный индустриальный университет”
Кафедра теоретической механики
КИНЕМАТИКА
Практикум для выполнения расчетно-графических работ
по дисциплине “Теоретическая механика”
Новокузнецк
2012
1
УДК 531 (075) К41
Рецензент:
доктор технических наук, профессор, зав. кафедрой теории механизмов и машин и основ конструирования СибГИУ
Л..Т. Дворников
К41 Кинематика: Практикум. / Сиб. гос. индустр. ун-т; сост.: Э.Я. Живаго, Н.И. Михайленко. – Новокузнецк: Изд. центр СибГИУ, 2012. – 128 с., ил.
Приводятся материалы для комплексной организации самостоятельной работы, в том числе методические рекомендации к решению задач по дисциплине “Теоретическая механика”, раздел “Кинематика”, излагается краткая теория, примеры решения и оформления задач, варианты заданий и ответы к ним, а также список рекомендуемой литературы.
Предназначены для студентов всех специальностей заочного вида обучения.
2
ПРЕДИСЛОВИЕ
Теоретическая механика как одна из естественных физико-мате- матических дисциплин занимает важное место в подготовке инженеров любой специальности. Для хорошего усвоения курса необходимо приобрести твердые навыки в решении конкретных задач, поэтому в учебных планах вузов выделяется достаточно большое количество часов на самостоятельную работу. В связи с этим назрела необходимость разработки многовариантных индивидуальных заданий по каждой теме.
Всборник заданий по кинематике включены методические указания по темам:
1.Кинематика точки.
2.Поступательное и вращательное движения твёрдого тела.
3.Сложное движение точки.
4.Плоскопараллельное движение твердого тела.
Вкаждой теме даётся краткая теоретическая часть. Большое место отведено примерам и методам решения задач. Решение задач сопровождается рядом указаний, которые должны помочь студенту при самостоятельном изучении материала. Кроме этого по всем темам и вариантам приведены ответы, что поможет студенту заранее убедиться в правильности решения задачи. В этой части сборник будет особенно полезен студентам заочной формы обучения.
Задачи подобраны частью из существующих учебных пособий без изменения или с частичными изменениями, частью предложены авторами сборника.
Авторы выражают признательность бывшим сотрудникам кафедры: Ш.Г. Володарской, К.С. Горбунову, Л.С. Молокову, М.А. Шинкареву, В.А. Черникову, Г.Т. Барановой, Н.И. Крестьяновой, которые в свое время принимали участие в подготовке заданий по некоторым темам.
Авторы выражают надежду, что предлагаемый сборник заданий будет полезен при организации самостоятельной работы студентов, как дополнение к существующим учебным пособиям.
3
КИНЕМАТИКА
Кинематикой называется раздел механики, в котором изучается движение материальных объектов с геометрической точки зрения, т.е. без учета их массы и действующих на них сил.
При изучении раздела выделяются кинематика точки и кинематика твердого тела.
Тема 1. КИНЕМАТИКА ТОЧКИ
Изучение движения точки заключается в определении характеристик её движения: положения точки в заданный момент времени в выбранной системе координат, траектории движения, скорости и ускорения.
Траекторией точки называется геометрическое место последовательных (с течением времени) положений её в пространстве, определяемое в той или иной системе отсчёта.
Кинематически задать движение (закон движения) точки – значит задать ее положение относительно выбранной системы координат в любой момент времени. Математические выражения, определяющие положение точки в любой момент времени в выбранной системе координат, называются уравнениями движения (законами движения) точки. Зная закон движения, можно определить основные кинематические характеристики движения.
Существует три основных способа задания движения точки: векторный, координатный и естественный.
При векторном способе задания движения положение точки задается её радиус-вектором r , как функцией времени, проведенным из какого-то неподвижного центра. Уравнение движения записывается в виде
r = r(t).
При координатном способе задания движения положение точки определяется её координатами в прямоугольной декартовой системе (рисунок 1.1). Координаты являются функциями времени, и уравнения движения точки записываются в виде
x = x(t), у = у(t), z = z(t).
4
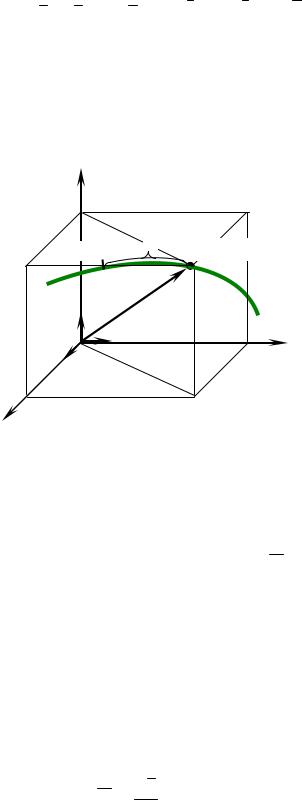
Очевидна связь между векторным и координатным способами задания движения
r = r(t), r = x i + у j + z k .
При естественном способе задания движения положение точки на заданной траектории определяется её дуговой координатой S = S(t ) (рисунок 1.1).
Задается начало отсчета (точка О1), положительное и отрицательное направления отсчёта дуговой координаты.
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
(−) |
O |
1 (+) |
S |
М(х,у,z) |
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
||||
|
|
|
|
|
k |
|
|
|
|
|
|
zM |
|
|
|
O |
|
j |
у |
||||||||
|
|
|
|
|
|
||||||||
i |
|
|
|
|
уМ |
|
xМ |
||||||
х |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Рисунок 1.1 – Естественный способ задания движения точки
Основными кинематическими характеристиками движения точки являются её скорость и ускорение. Это векторные величины имеющие размерности, соответственно, м/с и м/с2.
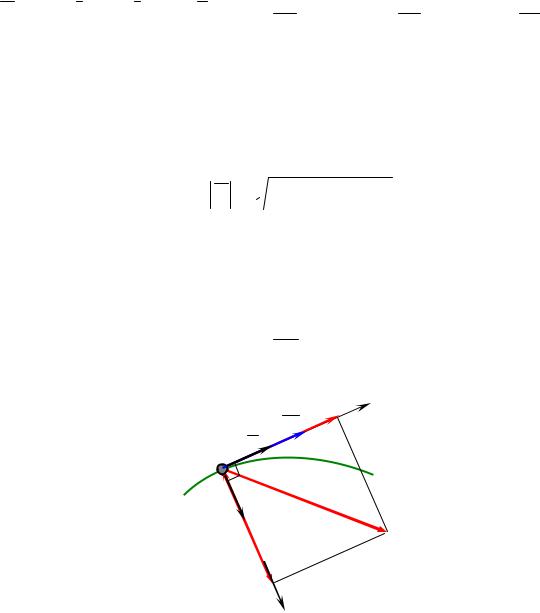
Скоростью точки называется вектор V , определяющий в каждый момент времени быстроту изменения положения и направление движения точки в выбранной системе отсчёта.
Вектор скорости точки в данный момент времени направлен по касательной к траектории (рисунок 1.2). При прямолинейном движении вектор скорости совпадает с траекторией и направлен в сторону движения.
При векторном способе задания движения скорость точки определяется как первая производная по времени от радиус-вектора
V = ddrt = r&.
При координатном способе задания движения скорость определяется через проекции вектора скорости на выбранные координатные оси
5
V=Vx i +V у j +Vz k , Vx = dxdt = x&, V у = ddуt = у&, Vz = dzdt = z&.
Проекция вектора скорости на координатную ось равна
алгебраическому значению первой производной по времени от соответствующей координаты точки.
Численное значение скорости определяется геометрическим сложением
V = V = 
Vx2 +V у2 +Vz2 .
При естественном способе задания движения числовое (или алгебраическое) значение скорости точки определяется как первая производная по времени от дуговой координаты
V = dSdt = S& .
aτ τ
М τ V
n
a
an n
Рисунок 1.2 – Скорость и ускорение точки
Ускорение точки a характеризует быстроту изменения вектора скорости по величине и направлению.
Вектор ускорения точки находится в соприкасающейся плоскости траектории точки, т.е. в плоскости Мτn (рисунок 1.2), и направлен в сторону вогнутости траектории. При прямолинейном движении вектор ускорения совпадает с траекторией движения точки.
При векторном способе задания движения ускорение точки равно или первой производной по времени от вектора скорости точки, или второй производной по времени от радиус-вектора точки
6
a = ddVt =V& = &r&.
При координатном способе задания движения ускорение точки определяется через проекции вектора ускорения на выбранные координатные оси
a =ах· i + ау· j + аz· k ,
ах = V&x = &x&, ау = V&у = &у&, аz =V&z = &z&, а = a = 
a x2 + a 2у + az2 .
При естественном способе задания движения ускорение точки проецируется на оси естественного трехгранника – на касательную ось Мτ и на главную нормаль Мn (рисунок 1.2)
a = aττ + an n или a = aτ + an ,
где τ и n − единичные векторы касательной и главной нормальной осей естественного трёхгранника.
Проекция ускорения точки на касательную ось aτ (касательное
ускорение) равна первой производной по времени от числового значения скорости точки или второй производной по времени от
дуговой координаты точки и характеризует изменение скорости по величине aτ =V& = S&&.
Проекция ускорения на главную нормальную ось an (нормальное ускорение) характеризует изменение вектора скорости
по направлению и определяется выражением an = V 2 , где ρ - радиус
ρ
кривизны траектории в данной точке. Так как aτ an , то а =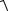 
aτ2 + an2 .
Если V = S& и aτ =V& = S&& имеют одинаковые знаки, то векторы V и aτ направлены в одну сторону, и движение точки будет ускоренным. В противном случае – движение точки замедленное.
Контрольные задания
По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = 1 с, определить положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
7
Примечания:
1. Номер варианта выбирается студентом по сумме двух последних цифр шифра.
2. Построение траектории, скорости и ускорения точки необходимо производить с соблюдением масштабов и при этом масштабы желательно выбирать так, чтобы изображаемые по одной прямой векторы имели различную длину.
Методические указания
1. Записать уравнение траектории точки в координатной форме y = f(x).
2. Определить, какая линия (или ее часть) является траекторией движения. Указать область значений, которые могут принимать координаты х и у.
3.Определить координаты точки в момент времени t1 = 1 c и показать ее на траектории движения.
4.Если точка попала на траекторию движения, то предыдущие три пункта выполнены правильно.
5.Определить скорость точки в заданный момент времени и
сделать графическую проверку. Для этого из положения М1 отложить Vx и Vy с учетом знаков (если проекция вектора на ось отрицательна,
то в сторону отрицательного отсчета, если положительна, то в сторону положительного отсчета). Если вектор V совпадает с касательной к траектории в этой точке, то скорость определена правильно.
6. Определить ускорение в момент времени t1 и сделать графическую проверку. Вектор ускорения а должен быть направлен
всторону вогнутости траектории.
7.Найти касательную и нормальную составляющие ускорения.
На рисунке |
спроецировать |
вектор а на |
оси |
естественного |
трехгранника |
Мτ и Мп. |
Длины векторов |
аτ |
и ап должны |
соответствовать рассчитанным параметрам.
8. Контролем правильности вычислений и построений ускорений является выполнение равенства ax i + ay j = an + aτ .
8
Примеры выполнения и оформления задач
Задача 1. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = 1 с, определить положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
Исходные данные: x = 2cos π4t см, y = 1 + 4sin π4t см, t = 1c.
Найти: у = ƒ(x); x; у; Vx; Vу; V; ax; aу; a; aτ ; an; ρ.
РЕШЕНИЕ:
1) Определяем траекторию точки М и её положение в данный момент времени.
Выражаем синус и косинус функции π4t , возводим их в квадрат и складываем. Получаем функцию:
x 2 |
+ |
( y −1) |
2 |
= 1. |
4 |
16 |
|
||
|
|
|
Траекторией точки является эллипс в пределах - 2 ≤ х ≤ 2 , -3 ≤ у ≤ 5 (рисунок 1.3).
При t = 1 c
х= 2 cos π4 =1,4 см, у = 1 + 4sin π4 = 3,8 см.
2)Определяем скорость точки:
Вектор скорости V =Vx i +V y j . Проекции вектора скорости:
& |
π |
sin |
πt |
, Vy = |
& |
πt |
, |
|
|
|
|||||
Vx = x = − |
2 |
4 |
y = π cos |
4 |
|||
при t = 1 c |
|
|
|
|
|||
|
|
|
|
|
|
|
Vx = − 12 π 0,7 = −1,1 см/с; Vy = π 0,7 = 2,2 см/с.
9