Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Индустриальный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МУ ТМ_2015 / Динамика Тема3 (Дрожжин, Михайленко)

.pdf

Скачиваний:

1607

Добавлен:

25.03.2016

Размер:

1 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра теоретической механики

ДИНАМИКА

Тема 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ

КИНЕТИЧЕСКОГО МОМЕНТА МЕХАНИЧЕСКОЙ СИСТЕМЫ

Методические указания для выполнения самостоятельной работы по дисциплине «Теоретическая механика»

для студентов очной формы обучения

УДК 378.147 Д44

Рецензент доктор технических наук, профессор,

заведующий кафедрой сопротивления материалов и строительной механики

Сибирского государственного индустриального университета А.Г. Никитин

Д44 Динамика. Тема 3. Теорема об изменении кинетического момента механической системы: методические указания /Сост. В.В. Дрожжин, Н.И. Михайленко: СибГИУ.− Новокузнецк, 2008.−39 с.

Методические указания включают краткую теоретическую часть, примеры решения задач, рекомендации по их решению, 25 вариантов индивидуальных комплексных заданий по 4 задачи в каждом варианте.

Рекомендуются для студентов очной формы обучения.

Новокузнецк 2008

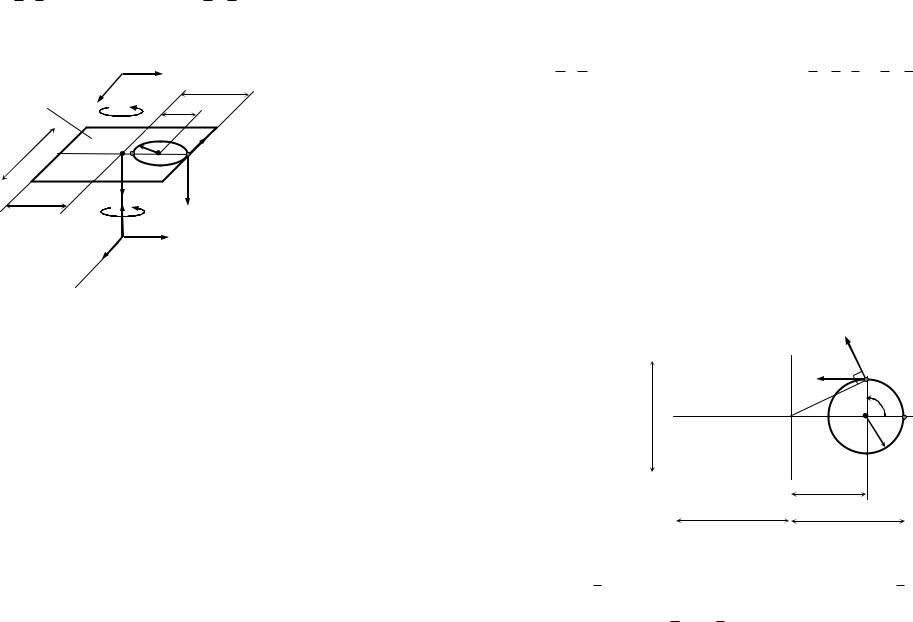
Момент количества движения материальной точки относительно центра и относительно оси

Моментом количества движения точки относительно

некоторого центра (О) называется векторная величина lO , определяемая

выражением

O ( mV )

mV .

(1)

В этом выражении

mV −

вектор

количества движения точки,

−

радиус-

вектор движущейся точки, проведенный из

выбранного центра О (рисунок 1). Вектор lO

строится в выбранном центре перпенди-

кулярно плоскости, в которой расположен

вектор mV и выбранный центр, и направлен

в ту сторону, откуда вектор

относи-

Рисунок 1	тельно центра виден направленным против

вращения часовой стрелки.
Момент количества движения равен взятому со знаком плюс или

минус произведению модуля вектора количества движения на плечо вектора mV относительно центра

h mV h .

(2)

где h – плечо вектора

коли-

чества движения точки,

равное

длине

перпендикуляра, опу-

щенного из выбранного центра

на линию

действия вектора

mV .

Величина

момента

количества движения, опреде-

mV1

ленная

по

выражению

(2) и

согласно

рисунку

будет

положительной.

Момент

количества

Рисунок 2

движения точки относитель-

но оси равен взятому со зна-

ком плюс или минус произведению проекции вектора mV на плоскость, перпендикулярную выбранной оси, на плечо этой проекции относительно

точки (О) пересечения оси с плоскостью (рисунок 2).

Обозначим mV ху mV1 .

lz mz mV					h1 .	(3)
		mV1

Момент количества движения точки относительно оси будет положительным, если с положительного направления оси движение точки видно происходящим против хода часовой стрелки (рисунок 2).

Понятие момента количества движения точки относительно центра и оси и правило знаков аналогичны понятиям момента силы относительно центра и оси.

Кинетический момент механической системы

Кинетическим моментом механической системы (моментом количества движения системы; главным моментом количества

движения) относительно некоторого центра О называется вектор LO ,

равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого центра.


	n			n
L	O		O ( mkVk )			(4)
L	O	m	O ( mkVk )		rk mkVk .	(4)
	k 1			k 1

где mk – масса произвольной материальной точки системы, Vk − скорость произвольной точки системы,

rk − радиус-вектор произвольной точки системы, проведенный из

выбранного центра.

Кинетическим моментом механической системы относи-

тельно оси называется алгебраическая сумма моментов количеств движения всех материальных точек системы относительно этой оси

n	n	n
Lx mx (mkVk ) , Ly my (mkVk ) , Lz mz (mkVk ) . (5)
k 1	k 1	k 1

Теорема об изменении кинетического момента механической системы

Производная по времени от кинетического момента механической системы относительно произвольного центра равна главному моменту внешних сил, действующих на систему, относительно того же центра


dLO
dLO	M	Oe ,	(6)
dt	M	Oe ,	(6)
dt

где MOe mO ( Fke ) .

k 1

Векторному равенству (6) соответствуют три равенства в проекциях на координатные оси:

dLx M xe mx Fke ,

dLу M eу

m у Fke ,

k 1

(7)

dLz M ze mz Fke .

k 1

Система уравнений (7) выражает теорему об изменении кинетического момента системы относительно координатных осей:

производная по времени от кинетического момента механической системы относительно какой-либо оси равна главному моменту внешних сил, действующих на систему, относительно той же оси.

Следствия из теоремы (законы сохранения кинетического момента)

1. Если главный момент внешних сил, действующих на механическую систему, относительно какого-либо центра, в течение некоторого промежутка времени, остается равным нулю, то кинетический момент системы относительно этого центра, в течении этого промежутка времени, остается неизменным, т.е. постоянным

MOe mO ( Fke ) 0				(8)
MOe mO ( Fke ) 0		dLO 0 LO const .		(8)
	n

	k 1		dt

2. Если главный момент внешних сил, действующих на механическую систему, относительно некоторой оси (например Ох), в течение некоторого промежутка времени, остается равным нулю, то кинетический момент системы относительно этой оси, в течении того же промежутка времени, остается неизменным, т.е. постоянным

M e	m F e 0 dLx 0			L		const .	(9)
	n				x
x	x	k
x	x	k	dt
	k 1		dt

Кинетический момент тела, вращающегося вокруг неподвижной оси

Твердое тело является частным случаем простейшей механической системы. Скорости точек вращающегося тела вычисляются как произведение угловой скорости тела на расстояние точки от оси вращения (радиус вращения) Vk rk . С учетом этого, согласно (5) имеем

	n			n		n		n
L m		(m V	) m V		r	m	r 2	m r 2 .
z	z	k k		k k	k	k	k	k к
	k 1			k 1		k 1		k 1

Здесь mk rk2 J z называется моментом инерции тела относительно оси

k 1

вращения.
Окончательно запишется
Lz Jz	(10)

Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

Подставим выражение (10) в систему уравнений (7)

dLz

тогда

(11)

J z mz Fk

или иначе Jz z mz Fk .

k 1

Уравнение (11) и есть дифференциальное уравнение враща-

тельного движения тела вокруг неподвижной оси Оz, где z

− угловое

ускорение тела, = (t) − уравнение вращательного движения тела вокруг неподвижной оси (угол поворота, угловая координата).

Пример 1. Тело 1 массой m1 вращается вокруг вертикальной оси Еz с постоянной угловой скоростью . В точке А желоба АВ, имеющего форму окружности радиусом R, центр которой отстоит от оси вращения на расстоянии ℓ находится материальная точка D массой m2. В некоторый момент времени на тело начинает действовать пара сил с моментом MZ. Через некоторый промежуток времени t1 действие пары сил прекращается, а точка D начинает двигаться вдоль желоба в направлении к точке В по закону AD = S(t).

Определить угловую скорость тела 1 при t1 и при t2, пренебрегая сопротивлением вращению. Тело 1 рассматривать как однородную прямоугольную пластинку, размеры которой указаны на рисунке (рисунок 3).

Дано: m1 = 100 кг, m2 = 10 кг, o = 5 рад/с; MZ = 8t Н м, t1 = 4 c,

	R	R 1
t2 = 5 c, AD = S =	2 t м, а 3 м,		м, 2 м.

Определить: 1 и 2.

РЕШЕНИЕ Применим теорему об изменении кинетического момента механи-

ческой системы, выраженную уравнением

dLz M ze mz Fke .
	n

dt	k 1

1. На систему за время от t = 0 до t1 действуют силы: G1 − сила тяжести тела 1, G2 − сила тяжести точки D, пара сил с моментом MZ, Е ,

Е , Е − реакции подпятника и H , H − реакции подшипника (рисунок

3).

Главный

момент

YН

внешних сил равен вра-

щающему

моменту

MZ,

так

как

другие силы

момента

X Н

ℓ

относительно

оси

не

создают (они либо парал-

лельны

оси

Ez,

либо

ее

О1

m V

пересекают).

А D

Предположим,

что

вращение тела 1 происходит

против хода часовой стрелки,

если

смотреть

со

стороны

положительного направления

Z Е

оси Ez.

YЕ

Х Е

Запишем выражение

кинетического

момента

системы,

который

склады-

Рисунок 3

вается из кинетического мо-

мента тела 1 (Jz ) и момента

количества движения точки D, находящейся в точке А тела 1.

Момент количества движения точки запишется

m V а m а2 .

Таким образом,

а2

( J

а2 ) .

Уравнение, выражающее теорему об изменении кинетического

момента, примет вид

d ((J

m a2 )щ)

M z ,

(a)

где М z 8t Н·м.

Разделим в уравнении (a) переменные и проинтегрируем левую и правую части уравнения

(J		m		a2 ) 1	d t1	8t dt , (J		m		a 2 )(		)	8t12	.	(b)
	z		2				z		2
											0	2
				0	0

Найдем численные значения входящих в уравнение (b) величин.

Момент инерции тела 1 относительно оси Еz, проходящей через центр масс

		m(4a2	a 2 )				5	m a2				5			32 375	кг м2,.
J		1							,	J				100
J	z								,	J	z			100
	z	12					12	1			z	12
		12					12					12
		J	z	m	2	а 2		375 10 32					465		кг м2.
			z		2

Подставляем в уравнение (b)

465 1 5 8 42 / 2 , отсюда 1 = 5,14 рад/с.

2. После прекращения действия момента MZ тело 1 вращается по инерции с угловой скоростью 1. В это время к системе приложены силы

G1 , G2 , реакции подпятника и подшипника Е , Е , Е , H , H .

Так как эти силы либо параллельны оси вращения, либо

пересекают ее,

то m ( F e ) 0

, т.е.

dLz

а это

значит,

что

k 1

Lz const .

Определим значения кинетических моментов

L1 при t

= t1 и

при t = t2 относительно оси вращения.

Для t = t1

L1 = (Jz + m2 a2) 1 = 465 5,14 = 2390,1 кг м2/с.

Найдем положение точки на траектории относительного

движения в момент времени t = t2.

S AD

R (t

t ) R (5 4) R м.

Угол , на который повернется радиус ОА, равен

m2Ve

m2Vr

О1

ℓ

Рисунок 4

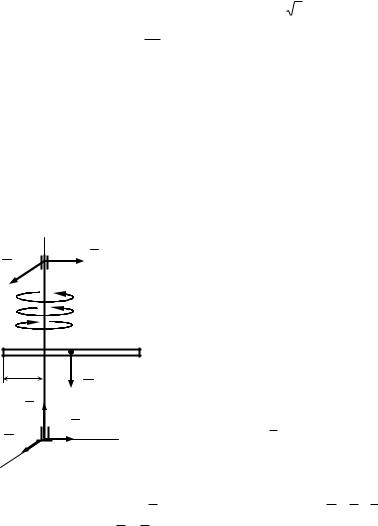
При t = t2 скорость точки D складывается из относительной скорости Vr по отношению к телу 1 и переносной скорости Vе в движении вместе с телом 1. Поэтому для t = t2 покажем два вектора количества движения точки: m2Vr и m2Vе на вспомогательном рисунке 4.

Для t = t	L J		2	m	( O D )2	m V OD.
2	2 z		2	2 2	1	2 r

Из рисунка 4

O O , a OD = R, тогда (O

D)2 = (O O)2 + (OD)2,

(O D)2

= ℓ2 + R2 = 22

+ 12 = 5 м2,

O D 5 м.

Скорость точки

V dS

R 1,57 м/с.

375 2 10 2

5 10 1,57 1 425 2

15,7.

Приравнивая L1

и L2 , находим 2

2390,1 425 2 15,7, 2

5,6 рад/с.

Ответ. 1 = 5,14 рад/с, 2

5,6 рад/с.

Пример 2. Тонкий однородный стержень АВ массой m и длиной ℓ

вращается вокруг вертикальной оси Еz, отстоящей от конца стержня на

расстоянии а, по закону = (t). Определить главный момент внешних

сил, действующих на систему в момент времени t

(рисунок 5). Массу

вертикального стержня ЕН не учиты-

вать.

X Н

YН

Дано: m =

кг, ℓ

= 0,4 м,

а = 0,1 м, 3 sin t рад, t = 1 c.

Определить: Мz.

РЕШЕНИЕ

Применим

дифференциальное

уравнение

вращения

твердого

тела

вокруг неподвижной оси:

Z Е

J z M ze ,

(a)

M ze

Fke − главный момент

Х Е

где

k 1

всех

внешних

сил

относительно

оси

вращения.

Рисунок 5

механической

системе

приложены

внешние

силы:

G −

сила

тяжести

стержня,

Е , Е , Е −

реакции

подпятника,

H , H −

реакции подшипника

и вращающий

момент Мz.

Главный момент внешних сил равен вращающему моменту

М z ,

так как другие силы моментов относительно оси Еz не создают (они либо

параллельны оси Еz, либо ее пересекают). Предположим, что вращение

стержня АВ происходит против хода часовой стрелки, если смотреть со

стороны положительного направления оси Еz, и будем считать это направ-

ление положительным направлением отсчета угла φ.

Согласно теореме о моменте инерции тела относительно оси, параллельной центральной (теорема Штейнера), момент инерции стержня АВ относительно оси вращения запишется

a)2 .

Момент инерции стержня относительно центральной оси

Подставляем численные значения величин

a)2

12 0,42

12(0,2 0,1)2 0,28 .

(b)

Так как угловая скорость и угловое ускорение стержня АВ

cos t

d 2

sin t

(c)

dt 2

то при t 1 = 1 с, 1 = 1,57 рад/с и 1 = − 2,85 рад/с2. Подставляем выражения (b) и (c) в уравнение (а)

M z 0,28 ( 2,85 ) 0,8 Н м.

Знаки Мz, , означают, что в данный момент времени, вращающий момент действует по направлению вращения часовой стрелки, а стержень продолжает вращаться против движения часовой стрелки и его движение замедленное.

Ответ. Мz = − 0,8 Н м.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Данная тема представлена 25 вариантами заданий, по четыре задачи в каждом. Рисунки к задачам по вариантам помещены на страницах

29 – 37.

Решать задачи рекомендуется в следующей последовательности:

выяснить вид движения тел и материальных точек, входящих в механическую систему, изображѐнную на рисунке. Если какие-либо точки системы совершают сложное движение, то необходимо установить относительное и переносное движения и на рисунке показать соответствующие векторы скоростей.

установить действующие на механическую систему внешние силы и изобразить их на рисунке.

освободить механическую систему от наложенных на неѐ внешних связей и показать на рисунке их реакции.

совместив одну из координатных осей с осью вращения

механической системы, записать теорему об изменении кинетического момента механической системы относительно выбранной оси (вторая и третья задачи) или дифференциальное уравнение вращательного движения тела относительно оси вращения (четвертая задача).

вычислить алгебраическую сумму моментов всех внешних сил, действующих на систему, относительно оси вращения. Если эта сумма равна нулю, то выполняется закон сохранения кинетического момента механической системы относительно выбранной оси. В этом случае следует вычислить кинетический момент системы в начальный и конечный моменты времени. Если закон сохранения кинетического момента системы относительно оси вращения не выполняется, то следует записать выражение кинетического момента для произвольного (текущего) момента времени.

дальнейший порядок решения определяется условиями задачи. В одних случаях может потребоваться интегрирование полученного дифференциального уравнения при заданных начальных условиях. В других случаях искомые величины могут быть найдены непосредственно из полученного дифференциального уравнения без его интегрирования (например, при определении углового ускорения тела по заданным силам, или при определении момента инерции тела по известным силам и закону движения и т.п.).

Примечание Необходимые для решения задач осевые моменты инерции однородных тел приведены в таблице A.1 справочного приложения A на странице 38.

ВАРИАНТЫ ЗАДАНИЙ

Задание 3.01

3.01.1. Однородное полукольцо 1 массой 100 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 20 кг движется относительно полукольца из точки А вдоль желоба АВ по закону АК = 0,75 Rt, (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 1 c, когда ω1 = 2 рад/с, если а = 1 м, b = 1,5 м, R = 1,2 м.

3.01.2.Деревянная доска длиной ℓ и массой m может вращаться без

трения вокруг горизонтальной оси ОО1. В центр доски попадает пуля массой m1, летевшая перпендикулярно к доске со скоростью V0. Определить угловую скорость, которую приобретет доска в момент удара пули. Доску считать однородным прямоугольником.

3.01.3.Цилиндр 1, масса которого 100 кг и диаметр d = 24 см, может свободно вращаться вокруг горизонтальной оси. На цилиндр

намотан трос, несущий на конце груз 2 массой 10 кг. Опускаясь, груз разматывает нить и вращает цилиндр. Определить угловое ускорение и угловую скорость цилиндра через t1 = 4 с после начала движения. Радиус инерции цилиндра относительно оси вращения ρ = 10 см.

3.01.4. Шкив массой 120 кг и диаметром 600 мм, представляющий собой однородный цилиндр, приводится во вращение из состояния покоя при помощи ременной передачи. Натяжение ветвей ремня считать постоянным и равным Т1 = 960 Н, Т2 = 480 Н. Пренебрегая трением в цапфах оси шкива, определить его угловую скорость через 3 с после начала движения.

Задание 3.02

3.02.1. Однородный диск 1 массой 80 кг и радиусом 2 м вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 10 кг движется относительно диска из точки А вдоль желоба АВ по закону АК = 0,5t2 (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 3 рад/с, если α = 120°.

3.02.2.Однородная прямоугольная пластинка, в которой имеется канал АВ, может вращаться без трения вокруг вертикальной оси Оz, совпадающей со стороной пластинки. В верхнюю точку А канала опущен без начальной скорости шарик К массой m. Определить угловую скорость пластинки в момент, когда шарик займет нижнее положение, если

угловая скорость пластинки в момент опускания шарика равнялась ωо, еѐ момент инерции относительно оси вращения Јо, а ширина пластинки а.

3.02.3.На барабан 1 массой m1 и радиусом R намотана нить с грузом 2 массой m2 на конце. Пренебрегая весом нити, определить угловое ускорение барабана при вертикальном движении груза, если радиус инерции барабана относительно его оси равен ρ и на барабан действует постоянный момент сил трения Мтр.

3.02.4.Однородный стержень ОА длиной ℓ и массой m, который может вращаться вокруг оси Ох, приведен в горизонтальное положение и отпущен без начальной скорости. Определить угловое ускорение стержня в зависимости от угла φ, если момент сил сопротивления в подшипнике О равен Мс = const.

Задание 3.03

3.03.1. Однородная пластинка 1 массой 60 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К мас-

сой 15 кг движется относительно пластины из точки А вдоль желоба АВ по закону АК = 0,6t (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 1 рад/с, если R = 1 м, α = 30°.

3.03.2.Однородный стержень АВ длиной 2ℓ и массой m1 подвешен в устойчивом положении равновесия на острие так, что его ось горизонтальна. Вдоль стержня могут перемещаться два шара 1 и 2, массой m каждый, прикрепленные к концам двух одинаковых пружин. Стержню сообщается вращательное движение вокруг вертикальной оси с угловой

скоростью соответствующей n1 оборотов в минуту, причем шары расположены симметрично относительно оси вращения и центры их с

помощью нити удерживаются на расстоянии 2ℓ1 друг от друга. Затем нить разрывается, и шары, совершив некоторое число колебаний, устанавливаются под действием пружин и сил трения в положение

равновесия на расстоянии 2ℓ2 друг от друга. Рассматривая шары как материальные точки и, пренебрегая массами пружин, определить новое число n2 оборотов стержня в минуту.

3.03.3.Тела 1 и 2, массы которых равны, соответственно, m1 и m2, подвешены к концам канатов намотанных на ступенчатый шкив. Под действием силы тяжести тело 1 перемещается по вертикали вниз, шкив вращается, а тело 2 поднимается. Определить ускорение тела 1, если задан момент инерции шкива относительно оси вращения J и радиусы r и R.

3.03.4.По заданному уравнению вращения φ = t3 − 5t2 (φ – рад, t – с) однородного цилиндра радиусом R = 1,41 м и массой 60 кг определить главный момент внешних сил, действующих на тело, в момент времени t = 2 с.

Задание 3.04

3.04.1. Однородная прямоугольная пластина 1 массой 120 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 12 кг движется относительно пластины из точки А вдоль желоба АВ по закону АК = 0,5t (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 4 c, когда ω1 = 2 рад/с, если а = 2 м, b = 1,5 м.

3.04.2. Вдоль образующей однородного кругового конуса массой m1, ось которого вертикальна, а вершина обращена вверх, просверлен канал. Конусу сообщают угловую скорость ω вокруг его оси и одновременно с

этим опускают в верхнее отверстие канала шарик К массой m, не сообщая ему начальной скорости. Какова будет угловая скорость конуса в момент выхода шарика из канала? Момент инерции конуса относительно вертикальной оси равен Јz = 0,3 m1 r2.

3.04.3. Ступенчатый шкив 3 приводится во вращение телом 1 массой m1, опускающимся под действием силы тяжести. При этом тело 2 массой m2 скользит по горизонтальной плоскости. Определить угловое ускорение шкива и ускорения тел, если момент инерции шкива относительно оси вращения J, даны радиусы r и R. Трением в подшипниках пренебречь. Коэффициент трения скольжения при движении тела 2 равен .

3.04.4. Однородный стержень АВ длиной 1 м и массой 2 кг вращается вокруг оси Oz из состояния покоя под действием пары сил с моментом Mz = 4t (Мz − Н·м, t – с). Определить в радианах угол поворота стержня в момент времени t = 2 с.

Задание 3.05

3.05.1.Однородный диск 1 массой 90 кг и радиусом R = 2,5 м вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 10 кг движется относительно диска из точки

Авдоль желоба АВ по закону АК = 0,25 t2 (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 4 рад/с, если r = 1,5 м.

3.05.2.Однородный круглый диск радиусом R и массой m вращается с угловой скоростью ω вокруг неподвижной оси О, перпендикулярной к его плоскости. В диске имеется канал ОА, внутри которого находится шарик К

массой m1 = 0,25m. Сначала шарик находится в середине канала и привязан нитью к точке O. В некоторый момент нить разрывается, и шарик начинает двигаться вдоль канала. Найти угловую скорость диска в момент, когда шарик достигнет точки А.

3.05.3.На шкив 2 радиусом R и массой m2, вращающийся вокруг неподвижной оси О, намотан канат, к концу которого подвешен груз 1 массой m1. Шкив приводится во вращение при помощи рукоятки OB = ℓ, к

концу которой приложена сила Q , перпендикулярная к рукоятке.

Пренебрегая массой каната и рукоятки, определить ускорение груза 1, если масса шкива равномерно распределена по его площади, а момент сил трения в подшипниках постоянен и равен Μтр.

3.05.4. К колесу 1 массой 60 кг и радиусом 25 см, вращающемуся

вокруг оси О с угловой скоростью ω = 10 рад/с, радиальной силой Q = 250 Н, прижимается тормозная колодка 2. Коэффициент трения скольжения f = 0,1. Пренебрегая трением в подшипниках вала колеса, определить, через сколько секунд после начала торможения, колесо остановится. Массу колеса считать равномерно распределенной по его ободу.

Задание 3.06

3.06.1. Однородный прямоугольник 1 массой 110 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 20 кг движется относительно прямоугольника из точки А вдоль желоба АВ по закону АК = 0,125 Rt2 (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 3 рад/с, если а = 1,6 м, b = 1 м,

R= 0,8 м.

3.06.2.Трубка 1 длиной ℓ вместе с шариком К, находящимся в ней на расстоянии а от конца О и привязанным нитью к этому концу, вращается в горизонтальной плоскости по инерции вокруг оси,

проходящей через точку О, с постоянной угловой скоростью ω0. Затем нить разрывают. Определить угловую скорость вращения трубки в тот момент, когда шарик вылетает из неѐ, если его масса m. Момент инерции трубки относительно оси вращения равен Ј.

3.06.3.Вал 1 радиусом R и массой m1 приводится в движение парой сил с постоянным моментом Μ, приложенной к рукоятке АВ.

Определить ускорение тела 2, если его масса равна m2, коэффициент трения скольжения − f, а радиус инерции вала − J. Трение в подшипниках вала не учитывать.

3.06.4.По заданному уравнению движения = 2sin0,5 t (φ – рад,

t – с) однородной прямоугольной плиты 1 с моментом инерции относительно оси вращения Jz = 10 кг·м2 определить главный момент внешних сил, действующих на тело, в момент времени t = l с.

Задание 3.07

3.07.1. Однородный диск 1 массой 80 кг и радиусом 2 м вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 20 кг движется относительно диска из точки А вдоль желоба АВ

по закону АК =	r	t	(АК – м, t – с). Определить кинетический момент
	9

механической системы относительно оси вращения в момент времени t1 = 3 c, когда ω1 = 2 рад/с, если r = 1,2 м.

3.07.2.Однородный диск 1 массой m1 и радиусом R вращается вокруг оси АВ с угловой скоростью ω. В некоторый момент от центра диска по его радиусу начинает двигаться материальная точка

Кмассой m2 с постоянной скоростью V . Определить угловую скорость диска по истечении времени t после выхода точки из центра О.

3.07.3.Четыре одинаковых точечных груза 1 массой m1 каждый вращаются с крестовиной в вертикальной плоскости. Расстояния от грузов до оси вращения одинаковы и равны ℓ. Крестовина приводится

в движение при помощи груза 3 массой m3, привязанного к канату, намотанному на барабан. Определить угловое ускорение барабана 2,

считая его однородным цилиндром массой m2 и радиусом R. Массой крестовины пренебречь. Момент сил трения в подшипниках вала барабана и крестовины постоянен и равен Μтр.

3.07.4.Маховик массой 5 кг вращается вокруг оси Oz по закону φ = 9t2 + 2 (φ – рад, t – с). Определить радиус инерции маховика, если его вращение вызвано действием вращающего момента Мz = 180 Η·м.

Задание 3.08

3.08.1. Однородный квадрат 1 массой 100 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 15 кг движется относительно квадрата из точки А вдоль желоба АВ по закону АК = 0,25 Rt2 (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 1 рад/с, если а = 1,2 м, R = 0,4 м.

3.08.2.Полому кольцу радиусом R сообщена некоторая угловая скорость вокруг вертикального диаметра. Внутри кольца из наивысшей точки движется шарик К массой m. Найти отношение наибольшей угловой скорости кольца к наименьшей. Момент инерции кольца относительно оси вращения равен Ј. Трением в подшипниках пренебречь.

3.08.3.Тело 1 массой m1, опускаясь по наклонной плоскости, приводит во вращение ступенчатый барабан, при этом тело 2 массой m2 поднимается. Определить ускорение тела 2, если коэффициент трения скольжения равен f, а момент инерции барабана относительно оси вращения − J. Угол наклона плоскости к горизонту α, радиусы r и R известны. Трением в подшипниках и массами канатов пренебречь.

3.08.4.Однородный диск радиусом R = 0,1 м под действием силы тяжести начинает вращение в вертикальной плоскости вокруг го -

ризонтальной оси Oz из положения, когда его радиус ОС горизонтален. Определить угловое ускорение диска. Трением в шарнире пренебречь.

Задание 3.09

3.09.1. Однородная прямоугольная плита 1 массой 50 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 10 кг движется относительно плиты из точки А вдоль желоба АВ по закону АК = 0,25t2 (АК – м, t – с). Определить кинетический момент механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 3 рад/с, если а = 2 м, b = 3 м.

3.09.2.Трубка 1 вращается вокруг вертикальной оси Oz, eѐ момент инерции Јz = 0,075 кг·м2. По трубке под действием внутренних сил системы движется шарик К массой 0,1 кг. Когда шарик находится на оси вращения, угловая скорость трубки ω = 4 рад/с. При каком расстоянии ℓ угловая скорость трубки станет равной 3 рад/с ?

3.09.3.Тело 1 массой 10 кг, опускаясь по гладкой неподвижной плоскости, с углом наклона α = 30°, приводит в движение тело 2 массой 1 кг посредством каната, перекинутого через блок С массой 24 кг и радиусом 0,6 м. Пренебрегая массой каната и предполагая, что масса блока равномерно распределена по его ободу, определить ускорение тела 2.

3.09.4.Для определения момента сил трения в цапфах на вал насажен маховик массой 50 кг, радиус инерции маховика относительно оси вращения равен 1,5 м. Маховику сообщена угловая скорость, соответствующая 240 oборотам в минуту. Предоставленный самому себе, он остановился через 10 минут. Определить момент сил трения, считая его постоянным.

Задание 3.10

3.10.1. Однородная пластина 1 массой 120 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 20 кг движется относительно пластины из точки А вдоль желоба АВ по закону АК = 0,75 t (АК – м, t – с). Определить кинетический момент рассматриваемой механической системы относительно оси вращения в момент времени t1 = 1 c, когда ω1 = 2 рад/с, если r = 1 м, R = 2 м.

3.10.2. Полое кольцо с отверстием в точке А может вращаться без трения вокруг вертикальной оси О1z. В отверстие опущен без началь-

ной скорости шарик К массой m. Определить угловую скорость кольца в момент времени, когда АОК = 60°,если вначале угловая скорость кольца равнялась ωо, момент инерции кольца относительно оси вращения Ј, радиус кольца R.

3.10.3.Тело 1 массой m1 поднимается с помощью каната, наматывающегося на ступенчатый барабан. К барабану приложена пара

сил с постоянным моментом Мвр. Определить ускорение тела 1, если масса противовеса 2 равна m2, момент инерции барабана относительно оси вращения J, радиусы r и R заданы.

3.10.4.Однородный шар с моментом инерции Jz = 4 кг м2 вращается вокруг оси Оz c угловой скоростью ω = 4,5 рад/с. Определить,

за какое время под действием вращающего момента Мz = 1,2 Н·м угловая скорость шара удвоится.

Задание 3.11

3.11.1. Однородный диск 1 массой 50 кг и радиусом 1 м вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 3 кг движется относительно диска из точки А вдоль желоба АВ по закону АК = 0,1t2 (АК – м, t – с). Определить кинетический момент рассматриваемой механической системы относительно оси вращения в момент времени t1 = 4 c, когда ω1 = 1 рад/с.

3.11.2.Стержень 1, изогнутый под прямым углом, может вращаться вокруг своей вертикальной стороны АО. На горизонтальную сторону ОВ свободно насажен груз 2, рассматриваемый как материальная точка массой m. В начальный момент груз находится на расстоянии а от точки

О, и система имеет угловую скорость ωо. Найти зависимость между угловой скоростью стержня и расстоянием х, если момент инерции стержня относительно оси АО равен Ј.

3.11.3.Груз 1 массой m подвешен на канате, намотанном на шкив, вращающийся вокруг неподвижной горизонтальной оси, проходящей через центр тяжести С шкива. При опускании груза шкив тормозится рычагом ОА, к концу А которого приложена вертикальная сила Q. Прене-

брегая массами рычага и каната, найти ускорение груза, если ОВ = 0,5АB, момент инерции шкива относительно оси вращения равен J

икоэффициент трения между рычагом и шкивом равен f.

3.11.4.Диск 1 радиусом R, прикрепленный к концу стержня 2 длиной ℓ, приводится во вращение вокруг вертикальной оси Ο1О2 с на-

чальной угловой скоростью ωо. Механизм помещѐн в сосуд с жидкостью. Равнодействующая сил сопротивления пропорциональна угловой скорости, перпендикулярна плоскости диска, приложена в его центре и равна F = αmω (m – масса диска, постоянный коэффициент пропорциональности). Определить, через какой промежуток времени угловая скороcть станет вдвое меньше начальной. Массу диска считать равномерно распределенной по его площади. Массой стержня пренебречь.

Задание 3.12

3.12.1. Однородный диск 1 массой 80 кг и радиусом 2 м вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 10 кг движется относительно диска из точки А вдоль желоба АВ по закону АК = 0,5 rt2 (АК – м, t – с).

Определить кинетический момент рассматриваемой механической системы относительно оси вращения в момент времени t1 = 1 c, когда ω1 = 3 рад/с, если r = 1 м.

3.12.2.На боковой поверхности кругового конуса 1 массой m расположены два тела 2 и 3, подвешенные на нитях одинаковой длины, закреплѐнных на оси вращения конуса Оz, и отстоящие от оси вращения конуса на расстоянии 0,3 радиуса основания. Конус вместе с телами вращался с угловой скоростью ω. После разрыва нитей тела начали опускаться по образующим боковой поверхности конуса. Определить угловую скорость конуса в момент, когда тела достигнут его основания. Масса каждого тела в 4 раза меньше массы конуса. Силами

сопротивления движению пренебречь. Тела считать точечными массами, момент инерции конуса относительно оси вращения Јz = 0,3mR2.

3.12.3.Момент М, вращающий барабан лебедки в период разгона, изменяется пропорционально времени, коэффициент пропорциональности

равен k. При этом тело 1 массой m1 поднимается по негладкой плоскости, наклоненной под углом α к горизонту. Определить закон изменения угловой скорости барабана 2 лебедки, считая его однородным

цилиндром массой m2 и радиусом R, пренебрегая массой каната. Момент трения в подшипниках барабана постоянен и равен Мтр, а коэффициент трения скольжения f.

3.12.4.Однородный стержень 1 длиной 1,5 м, масса которого 8 кг,

вращается вокруг	оси Оz	под действием пары	сил с	моментом
М = 12sin0,75 t (М − Н·м, t – c).
Определить	угловое	ускорение стержня в	момент	времени
t = 0,6 с. Трение в подшипниках не учитывать.
				19

Задание 3.13

3.13.1. Однородное треугольное тело 1 массой 90 кг вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка К массой 15 кг движется относительно тела из точки А вдоль желоба АВ по закону АК = 0,3t2 (АК – м, t – с). Определить кинетический момент рассматриваемой механической системы относительно оси вращения в момент времени t1 = 2 c, когда ω1 = 1 рад/с, если а = 1 м, b = 1,2 м, α = 30°.

3.13.2.Однородный диск 1 массой m1 и радиусом R, в котором имеется прямолинейный канал АВ, может вращаться без трения вокруг вертикальной оси Оz. В момент, когда диск вращается с угловой скоростью ω, в верхнюю точку канала опускают без начальной скорости

шарик К массой m2. Определить угловую скоростью диска в момент времени, когда шарик займет нижнее положение. Шарик принять за материальную точку.

3.13.3.На ступенчатый шкив, вращающийся вокруг неподвижной горизонтальной оси О, намотаны два каната, несущие на концах грузы

1 и 2, массы которых равны, соответственно, m1 и m2. Груз 1 опускается по наклонной плоскости, а груз 2 поднимается по другой наклонной плоскости. Канаты образуют с вертикалью углы α и β. Κ шкиву приложен постоянный момент Μ. Определить угловое ускорение шкива, если заданы радиусы r и R, момент инерция шкива относительно оси вращения J и коэффициенты трения скольжения f1

иf2 грузов о соответствующую наклонную плоскость.

3.13.4.Однородный диск массой 80 кг и радиусом R = 0,5 м

вращается вокруг горизонтальной оси Oz под действием пары сил с моментом М = 20 t2 (М − Н·м, t – c). 0пределить угловую скорость диска в

момент времени t = 6 с, если его начальная угловая скорость ω0 = 0. Трением в подшипниках пренебречь.

Задание 3.14

3.14.1.Однородный диск 1 массой 100 кг и радиусом 1,6 м вращается вокруг вертикальной оси Оz с угловой скоростью ω. Материальная точка

Кмассой 20 кг движется относительно диска из точки А вдоль желоба АВ по закону АК = 0,4t (АК – м, t – с). Определить кинетический момент рассматриваемой механической системы относительно оси вращения в момент времени t1 = 3 c, когда ω1 = 3 рад/с, если α = 60°.

3.14.2.Резервуар 1, момент инерции которого относительно вертикальной оси Οz равен 1 кг·м2, вращается с угловой скоростью

1 / 21 2 > Следующая >>>

Соседние файлы в папке МУ ТМ_2015

#
25.03.20161 Mб1607Динамика Тема3 (Дрожжин, Михайленко).pdf
#
25.03.20161.05 Mб54Кинематика (Живаго, Михайленко).pdf
#
25.03.2016430.62 Кб92Кинематика Т.1 (Живаго, Желтухин, Ермаченко).pdf
#
25.03.2016512.84 Кб60Кинематика Т.2 (Живаго, Дадочкина, Ермаченко, и др.).pdf
#
25.03.2016340.59 Кб51Кинематика Тема1 (Живаго, Михайленко).pdf
#
25.03.2016408.23 Кб53Кинематика Тема2 (Живаго, Михайленко).pdf