Soprotivlenie_materialov

1. Сопротивление материалов – это наука о методах расчета элементов инженерных конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности.

2. Утверждение, что напряжения и перемещения в сечениях, удаленных от места приложения внешних сил, не зависят от способа приложения нагрузки, называется принципом Сен-Венана.

3. Тело, один размер которого намного превышает два других, называется стержнем.

4. Силы взаимодействия между частями рассматриваемого тела называются внутренними.

5. Полное напряжение в точке сечения, в общем случае, раскладывается на нормальное и касательное напряжения.

6. Распределение нормальных напряжений при растяжении – сжатии вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения существенно зависит от величины приложенных сил.

7. Первоначальная длина стержня равна l. После приложения растягивающей силы длина стержня стала l(1). Величина называется абсолютным удлинением.

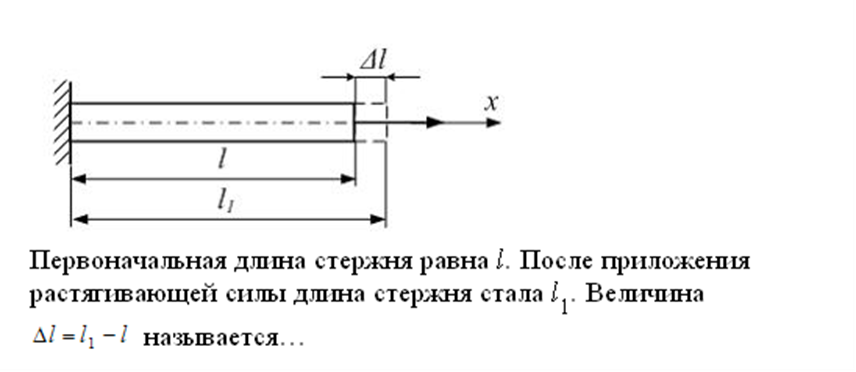
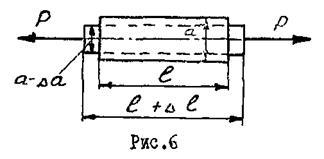
8. Коэффициентом Пуассона называется отношение относительной поперечной деформации к относительной продольной деформации.

9. К стержню квадратного поперечного сечения приложены одинаковые растягивающие силы. Если одновременно увеличить в 2 раза длину стержня и размер стороны, абсолютное удлинение стержня уменьшиться в 2 раза.

10. Какие деформации называются упругими? Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки.

11. Какие деформации называются остаточными (пластическими)? Деформация пластической, если после снятия нагрузки она не исчезает.

12. В чем сущность метода сечения? Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

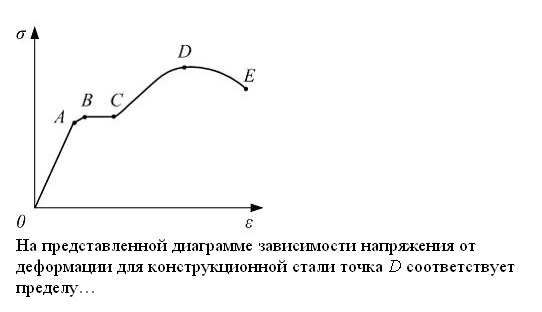
13. На представленной диаграмме зависимости напряжения от деформации для конструкционной стали точка D соответствует пределу прочности(разрешающей нагрузки).

14. Допускаемое напряжение (S)=160Мпа. Диаметры круглых поперечных сечений стержней d(1) и d(2) в мм будут равны 20,4 21,85.

15. Стержень нагружен системой сил. Модуль упругости материала E, площадь поперечного сечения A, размер a, значения силы F заданы. Продольная линейная деформация на участке CK равна 2F/EA.

16. Как формулируется закон Гука? Закон Гука — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе.

17. Что называется коэффициентом поперечной деформации? Коэффициент Пуассона.

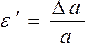
18. Какие задачи называются статически неопределимыми? Задачи, в которых все реакции связей определяются из условий равновесия, называются статически определимыми. Если число неизвестных реакций превышает число уравнений равновесия, то задача становиться СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ.

19. Что называется пределом пропорциональности, пределом упругости, пределом текучести, пределом прочности?

1: Предел абсолютной упругости.

2: Предел пропорциональности.

3: Предел упругости.

4: Предел текучести.

20. Стержень с квадратным поперечным сечением нагружен силой F=1000kH. Модуль упругости материала E=200 Гпа. Допустимое напряжение (S)=100 Мпа. Допустимое минимальное перемещение верхнего сечения (S)=0,0001L. Допустимый размер поперечного сечения из условия жесткости равен 0,707 квадратных метров.

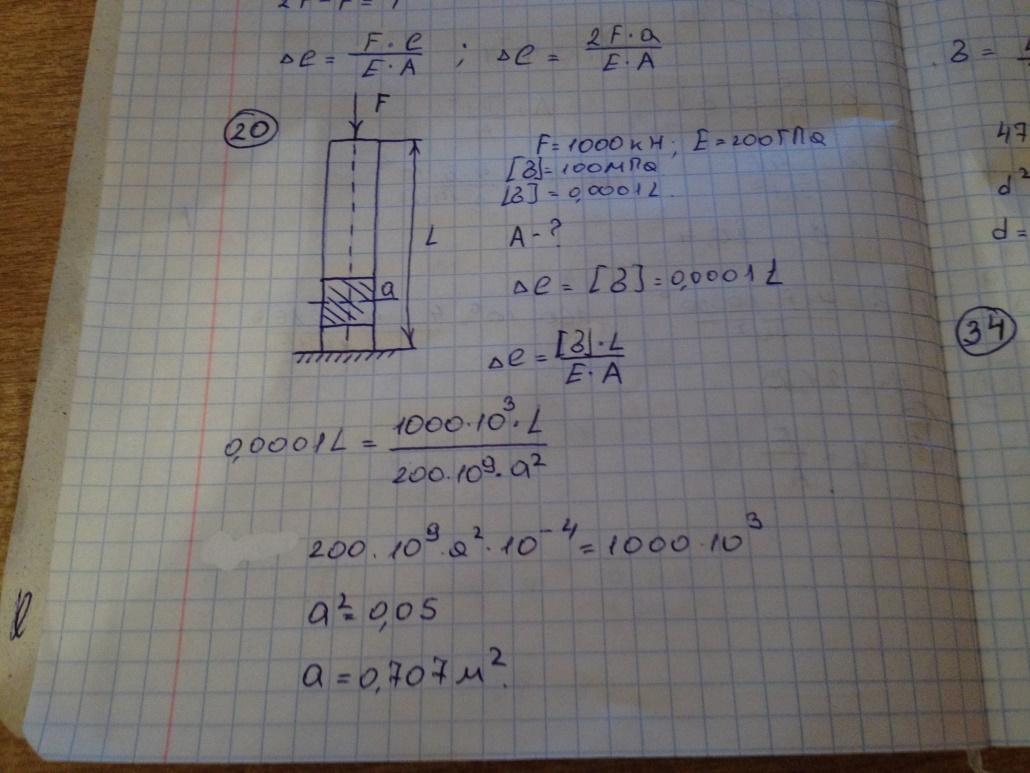
21. Допускаемое напряжение на растяжение – сжатие для материала равно 150 Мпа. Для стрежня круглого поперечного сечения наименьший диаметр D из условия прочности равен 0,0834 квадратных метров.

22. В чем разница между пластичными и хрупкими материалами? Образцы из хрупких материалов ( например, из серого чугуна) разрушаются при весьма малых деформациях, а из пластичных материалов ( например, из малоуглеродистой стали) - при значительных деформациях.

23. Что называется коэффициентом запаса прочности? Коэффициент запаса — величина, показывающая способность конструкции выдерживать прилагаемые к ней нагрузки выше расчётных.

где S — предельно допустимое значение рассматриваемой величины (силы, напряжения, перемещения и т. д.);

T — расчетное значение этой величины.

24. Как формулируется условие прочности при любом виде де-формации?

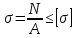
25. Что такое жесткость поперечного сечения? Жёсткость — это способность конструктивных элементов сопротивляться деформации при внешнем воздействии.

26. Что характеризует величина Е? Модуль упругости материала.

27. При расчете заклепки на срез величина площади среза равна

;m=2

Ответ:

28. Что называется абсолютным и относительным сдвигом?

Относительный сдвиг является угловой деформацией, характеризующей перекос элемента.

29. Как формулируется закон Гука при сдвиге?

30. Какова формула связи трех упругих констант (E, G и µ)?

31. Из расчета на срез минимальная высота головки болта при заданных значениях d и равна

При малой высоте головки болта происходит ее срез по цилиндрической поверхности диаметром d. Примем, что касательные напряжения постоянны по высоте h головки.

Ответ: h=

32. При кручении максимальное касательное напряжение возникает в точке D

Ответ: Точка D

33. Из условия жесткости в заданных сечениях (а) и G , наименьший допускаемый диаметр вала равен

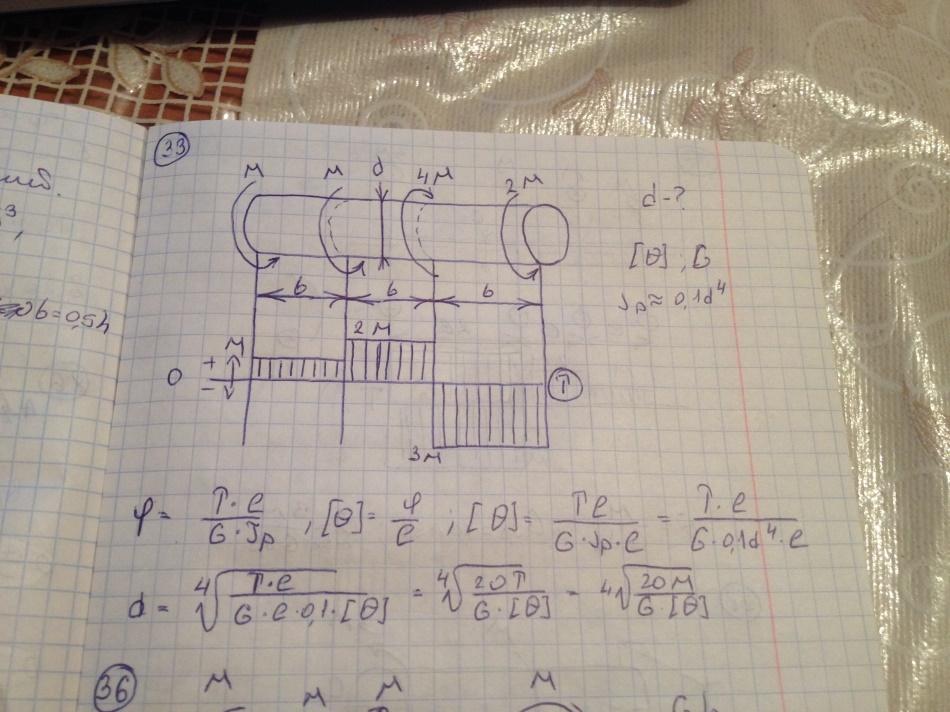
34. Труба испытывает деформацию кручение. Эпюра распределения касательных напряжений в поперечном сечении трубы имеет вид:

35. При деформации кручение угол взаимного поворота двух сечений, отнесенный к расстоянию между ними, называется относительным углом закручивания.

36. Тогда максимальный угол закручивания равен:

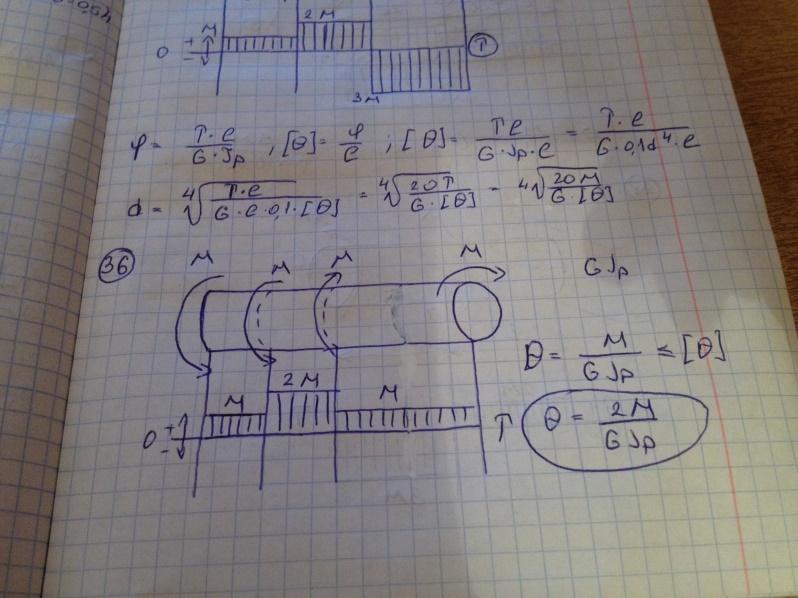
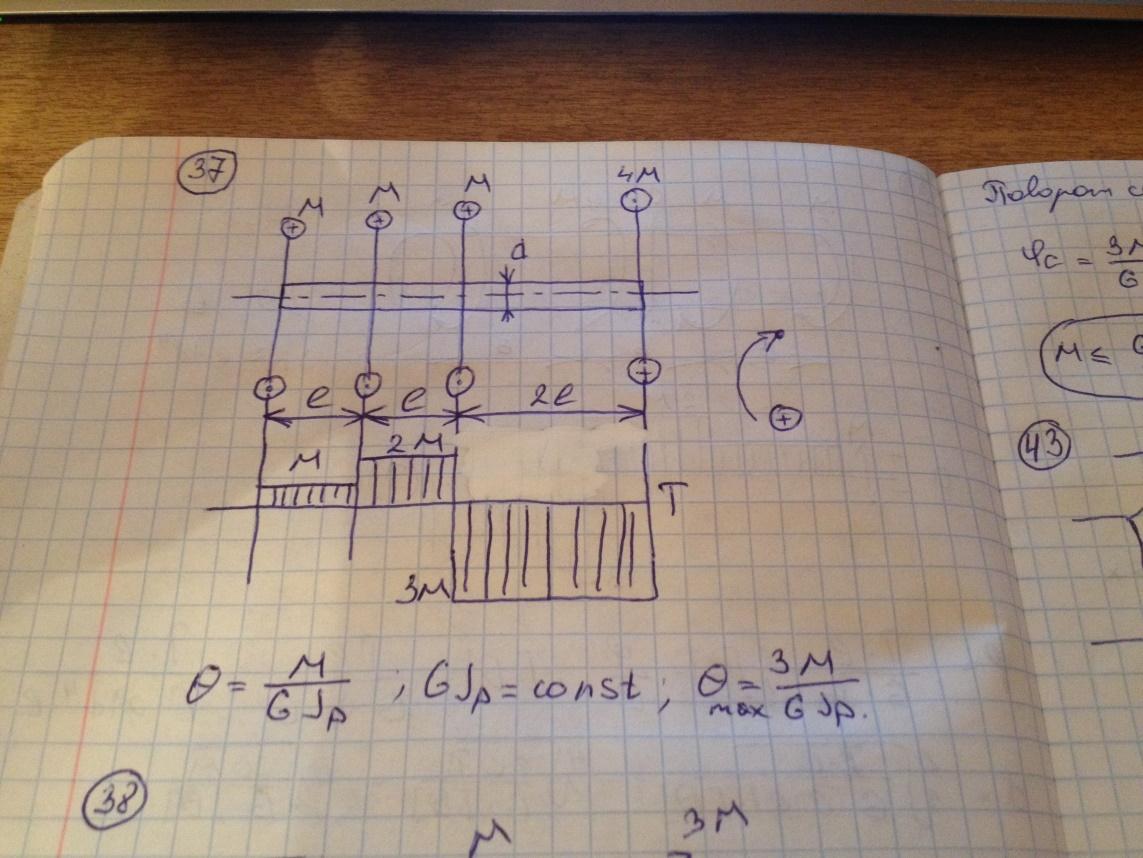
37. Стержень круглого сечения диаметром d нагружен, как показано на рисунке. Максимальное значение угла закручивания равно

Модуль сдвига материала G, значение момента М и длина l заданы.

38. Схема нагружения показана на рисунке. Длина L, жесткость поперечного сечения стержня на кручение , допускаемый угол поворота сечения C заданы. Из расчета на жесткость максимально допустимое значение внешней нагрузки M равно (Эпюра наоборот, поменять плюс с минусом)

39. Правила построения эпюр крутящих моментов?

Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным - в противном случае.

40. Какие напряжения возникают в поперечном сечении круглого стержня при кручении и как они направлены?

В поперечных сечениях бруса при кручении возникают касательные напряжения, направление которых в каждой точке перпендикулярно к радиусу, соединяющему эту точку с центром сечения, а величина прямо пропорциональна расстоянию точки от центра.

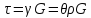
41. Чему равен полярный момент инерции круглого сечения?

42. Что называется моментом сопротивления при кручении?

Полярный момент сопротивления (или момент сопротивления при кручении), является геометрической характеристикой поперечного сечения вала, определяющей способность вала сопротивляться кручению. Полярный момент сопротивления измеряется в единицах длины в кубе (в см3).

Для стержня круглого поперечного сечения полярный момент сопротивления определяется формулой:

.

Для полого вала, имеющего внутренний диаметр d и внешний – D, полярный момент сопротивления выражается формулой:

, где .

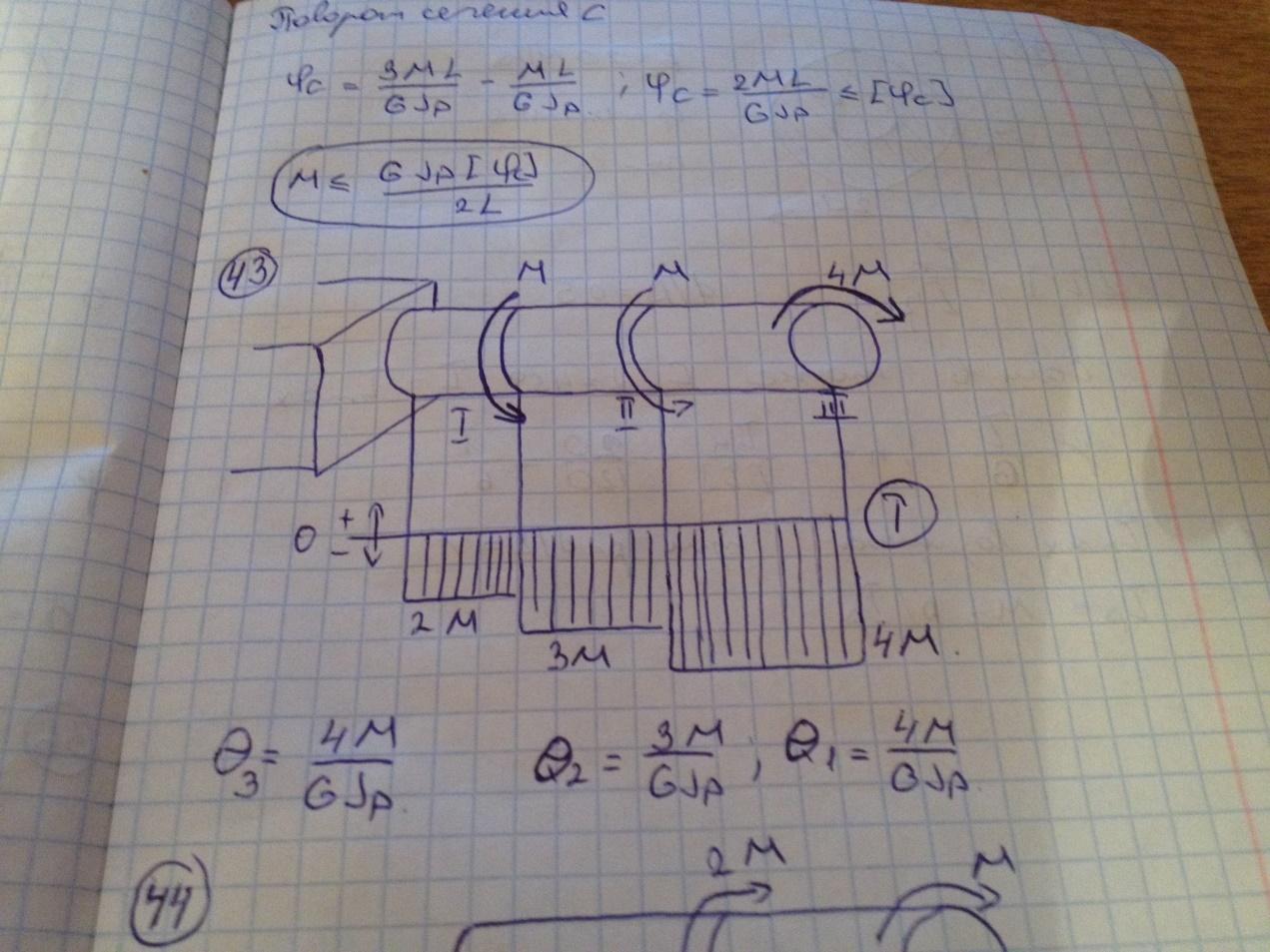
43. Максимальный относительный угол закручивания имеет место на участке номер 3. (исправить эпюру, все моменты вверху)

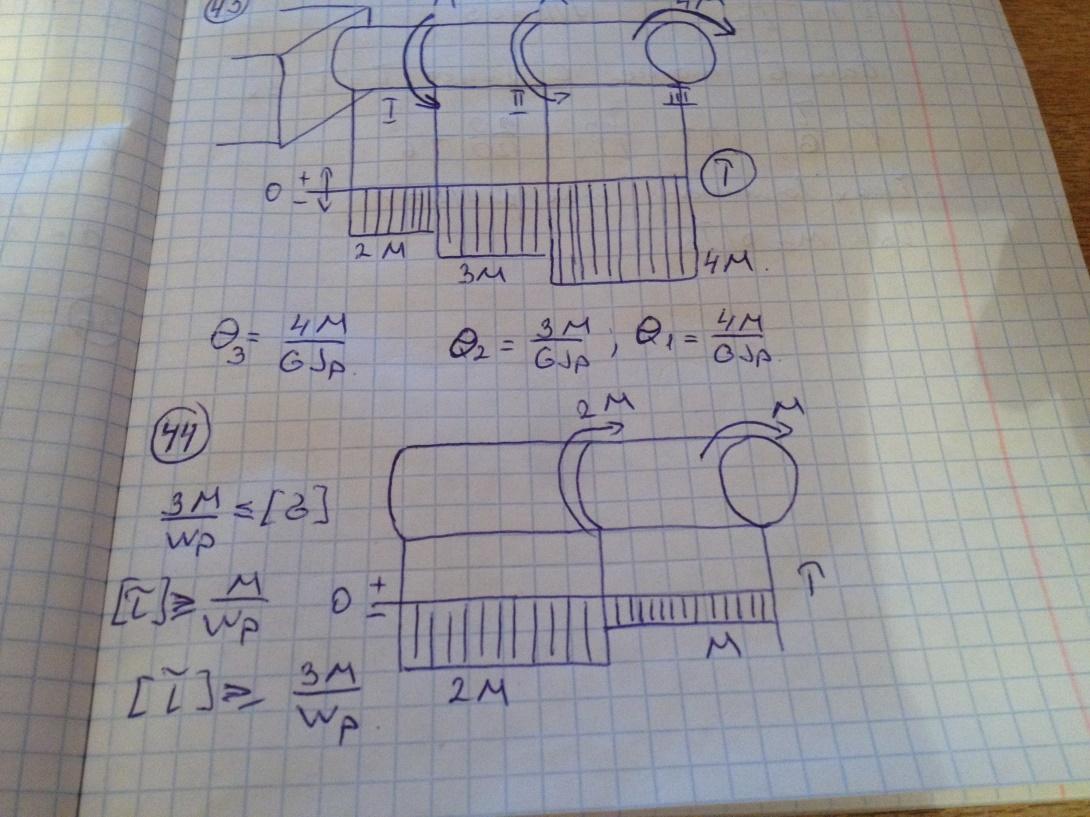
44. Условие прочности для стержня имеет вид:

45. Труба испытывает деформацию кручение. Касательное напряжение в точке C поперечного сечения трубы равно 20Мпа. Предел текучести материала трубы при чистом сдвиге коэффициент запаса прочности равен

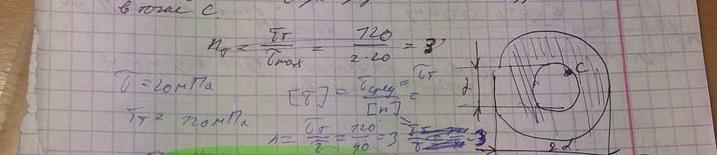
46. Что называется полным и относительным углом закручивания бруса? Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания.

47. Как производят расчет вала на прочность?

Используя формулу для максимальных касательных напряжений, можем записать условие прочности при кручении

Wp – полярный момент сопротивления.

48. Как производят расчет вала на жесткость?

Условие жесткости требует, чтобы максимальный относительный угол закручивания θmax, вычисленный по формуле, был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

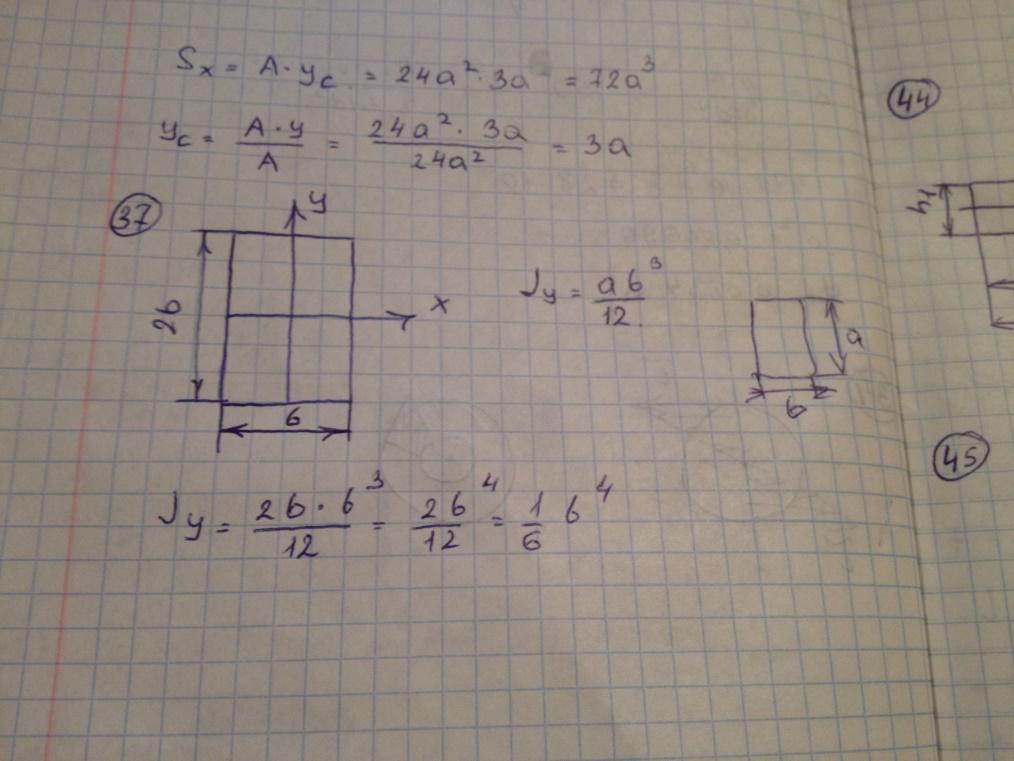
49. Статический момент площади сечения относительно оси x равен

50. Осевой момент инерции площади сечения относительно оси y равен

51. Для сечения известны осевые моменты инерции сечения относительно осей , , 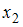: , , 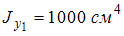. Осевой момент инерции относительно оси равен…

52. Что такое 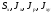и их единицы измерения?

1. Статический момент сечения, ед. измерения см^3;

2. Осевой момент инерции, ед. измерения см^4;

3. Полярный момент инерции, ед. измерения см^4;

4. Центробежный момент инерции, ед. измерения см^4.

53. Чему равен статический момент сечения относительно оси, проходящей через центр его тяжести? Равен нулю.

54. Формулы для определения осевых моментов инерции относительно центральных осей круга, прямоугольника, кольца?

1. Круг

2

2. Кольцо

3. Прямоугольник

55. Если в плоскости сечения несколько параллельных осей, относительно какой из них равен минимальному значению?

56. Что такое главные моменты инерции? Главными осями называются такие оси координат, относительно которых центробежный момент инерции равен нулю. Моменты инерции относительно главных осей инерции сечения называются главные моменты инерции сечения.

57. Осевой момент инерции сечения относительно оси х равен

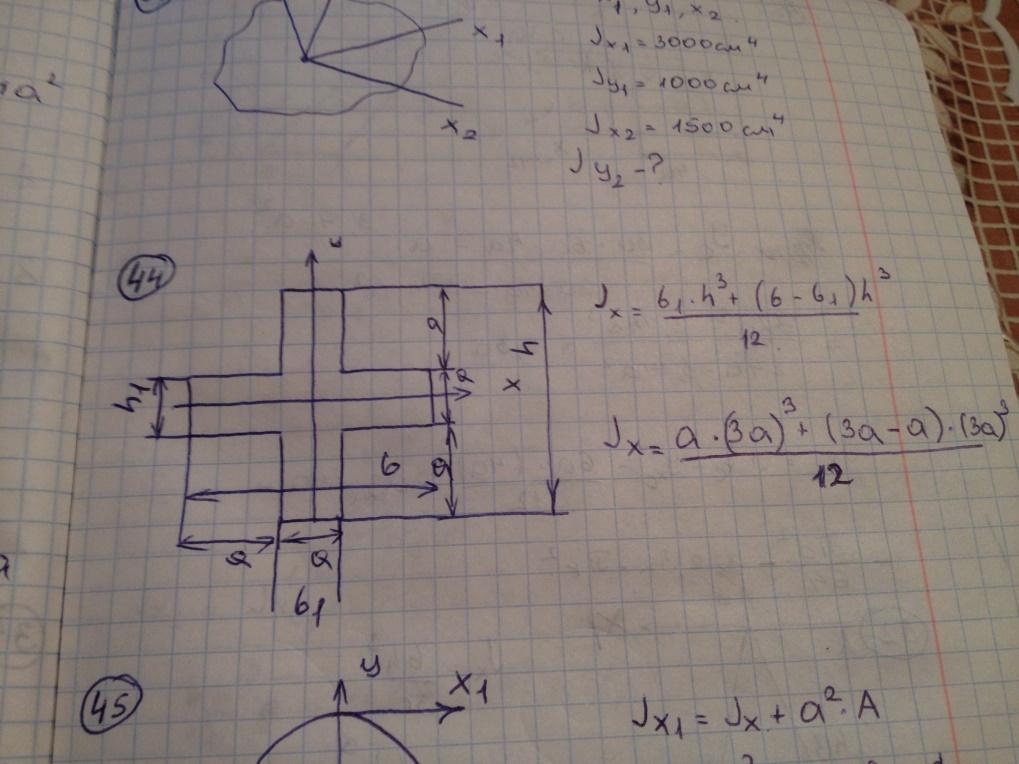
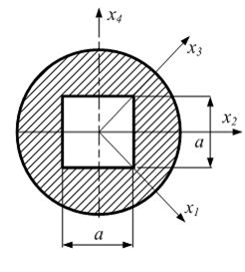
58. Из указанных центральных осей главными осями сечения являются х3 и х1

59. Из указанных центральных осей сечения равнобокого уголка главными являются х3 и х1

60. Какие оси называются главными и главными центральными осями инерции? Главными осями называются такие оси координат, относительно которых центробежный момент инерции равен нулю. Главными центральными осями называются оси, проходящие через центр тяжести сечения.

61. Чему равен относительно главных осей инерции? Равен нулю.

62. В каких случаях без вычисления можно установить положение главных осей инерции сечения? Если фигура имеет ось симметрии.

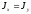63. Если и , то какие оси сечения являются главными?

64. Ось, относительно которой статический момент площади сечения равен нулю, называется главной центральной осью.

65. Если , то значение осевого момента инерции площади

66. Статический момент площади сечения относительно оси x равен нулю.

67. Поперечное сечение балки составлено из вертикального листа и четырех неравнобоких уголков 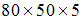. Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения и соответственно равны

8

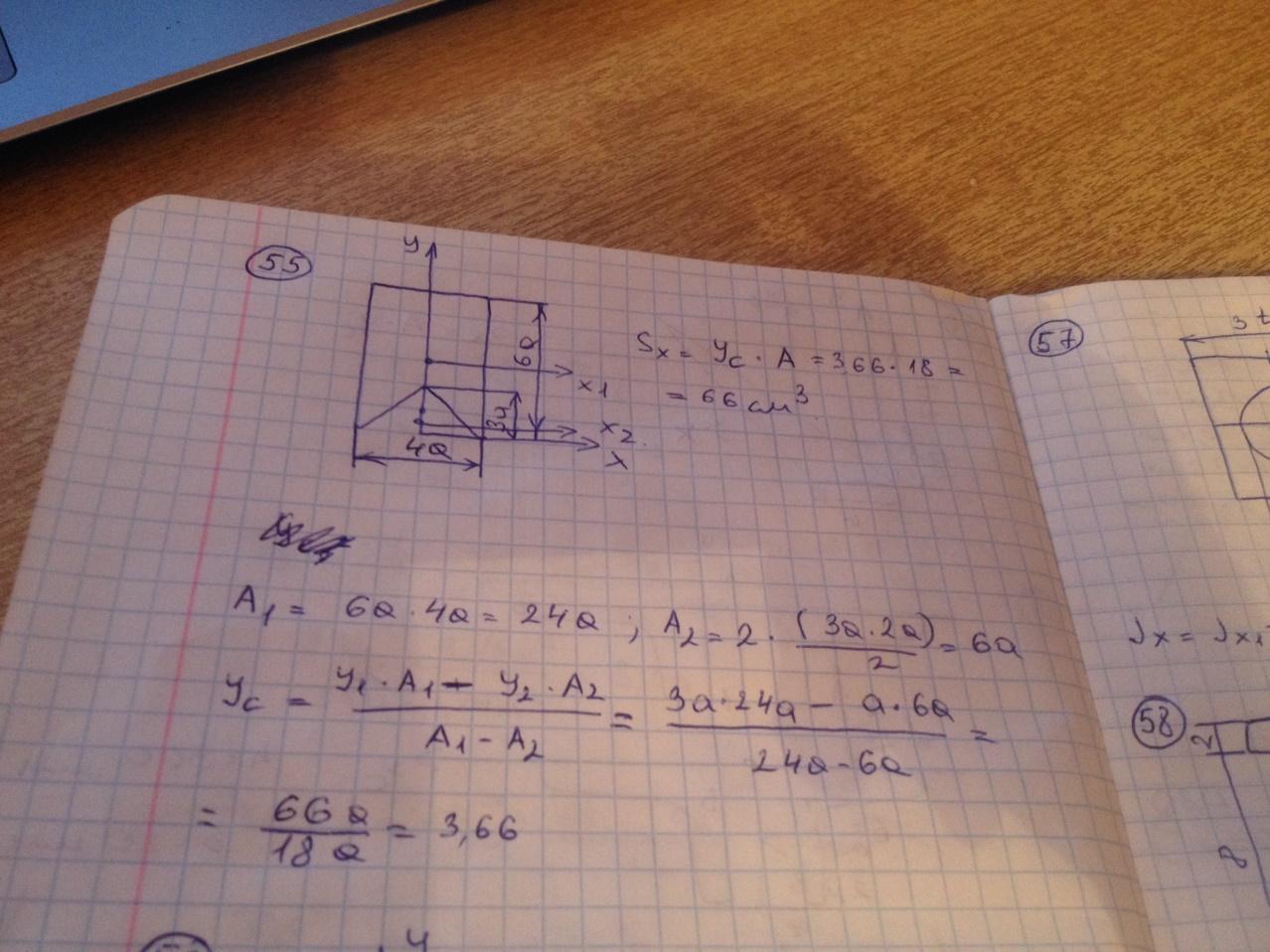
68. Статический момент площади сечения относительно оси x равен…

69. Осевой момент инерции сечения относительно оси 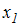равен

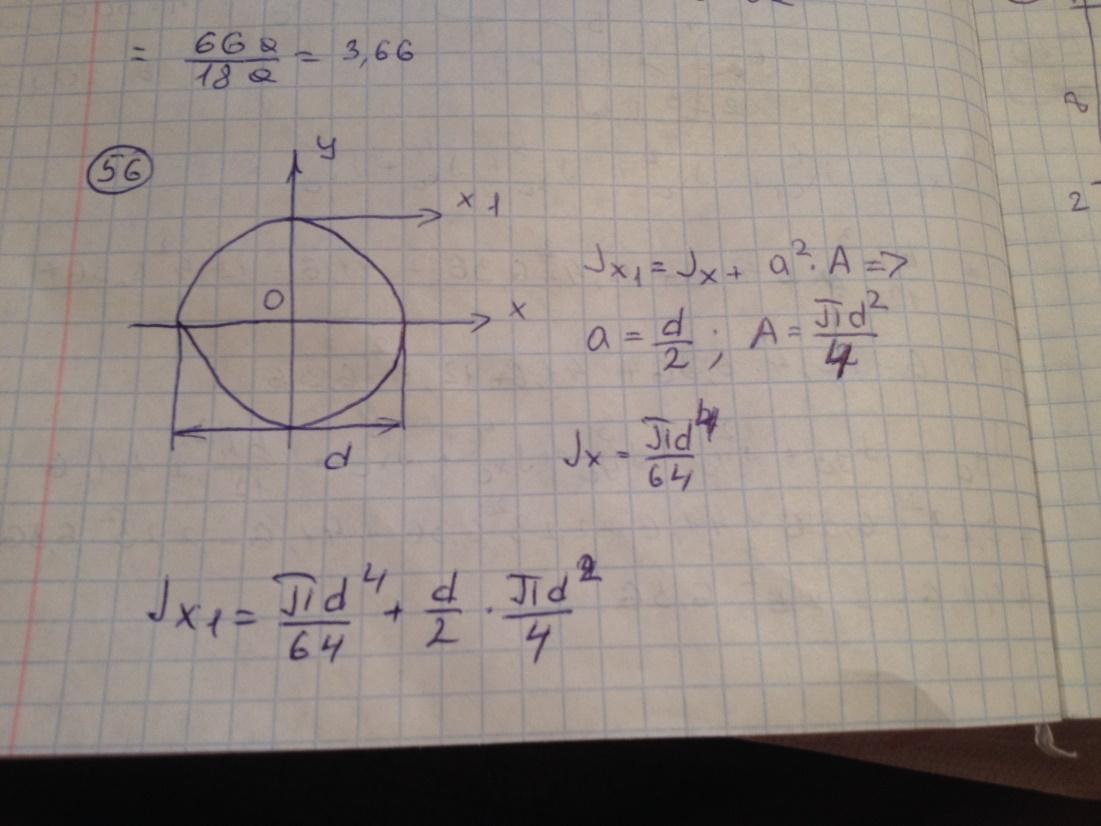
70. Момент инерции площади фигуры относительно оси x, проходящей через центр тяжести фигуры, равен

71. На рисунке размеры поперечного сечения заданы в см. Осевой момент инерции сечения относительно центральной оси x равен

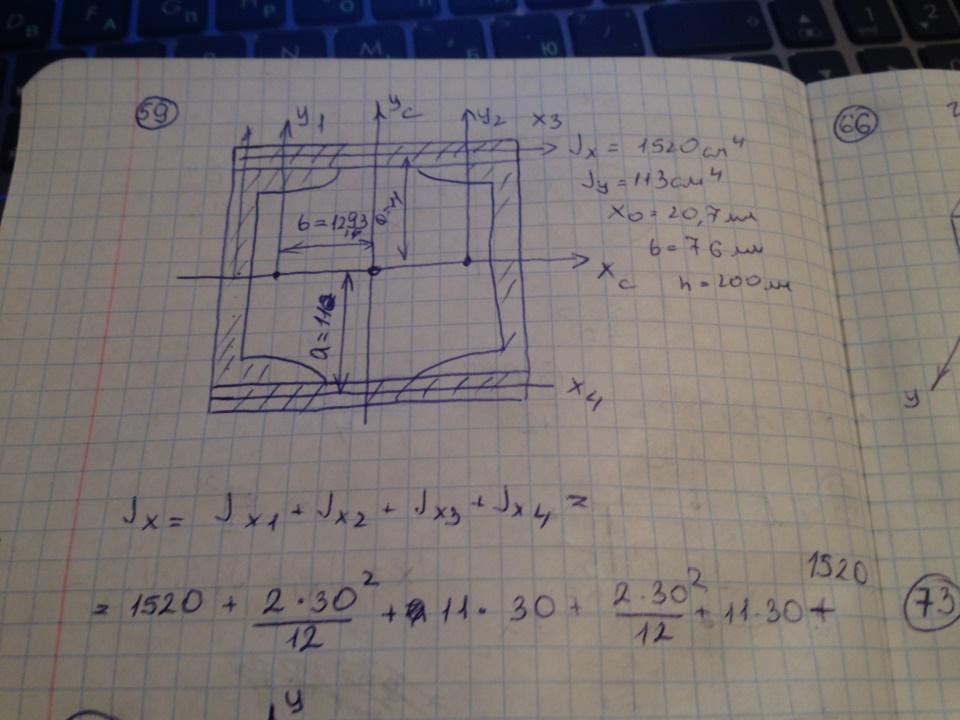
72. Поперечное сечение балки составлено из двух швеллеров №20 и листов, прикрепленных с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси x равен

73. Момент инерции сечения относительно оси х равен, Координата центра тяжести фигуры равна

74. Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций имеет название обобщенного закона Гука.

75. Правило, согласно которому на взаимно перпендикулярных площадках элемента, выделенного из тела, касательные напряжения равны по величине и направлены к общему ребру (или от него), называют законом парности касательных напряжений.

76. Напряжение состояние «чистый сдвиг» показано на рисунке 3.

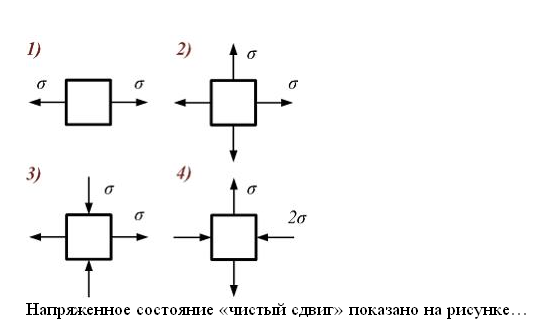
Решение:

  Чистый сдвиг – напряженное состояние, когда на гранях выделенного элементарного объема действуют только касательные напряжения. Если элементарный объем повернуть на угол, равный  , то касательные напряжения на его гранях (площадках) будут равны нулю, но появятся нормальные (главные) напряжения  и  . Таким образом, чистый сдвиг может быть реализован растяжением и сжатием в двух взаимно перпендикулярных направлениях напряжениями, равными по абсолютной величине. Следовательно, напряженное состояние «чистый сдвиг» показано на рисунке 3.

77. Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями.

78. На гранях элементарного объема (см. рисунок) определены значения напряжений в МПа. Угол между положительным направлением оси x и внешней нормалью к главной площадке, на которой действует минимальное главное напряжение, равен -22 градуса 30 минут.

79. Какие имеются виды напряженного состояния материала?

а – линейное; б – плоское; в – объемное

80. Объемный элемент находится под действием нормальных напряжений, показанных на рисунке: , , . Модуль упругости материала , коэффициент Пуассона . Линейная деформация в направлении оси z будет равна нулю, когда 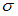принимает значение 25Мпа.

81. На гранях элементарного объёма действуют напряжения, заданные в Мпа. Напряженное состояние в точке где только одно нормальное напряжение.(Линейная деформация)(Сжатие)

82. Изотропный материал на растяжение и сжатие работает неодинаково. Для оценки прочности материала при сложном напряженном состоянии используется теория О. Мора.

При оценке прочности материала, неодинаково работающего на растяжение и сжатие, используют теорию прочности О. Мора. Эквивалентное напряжение по данной теории определяют по формуле  . Коэффициент «k» для пластичного материала равен отношению предела текучести при растяжении к пределу текучести при сжатии, 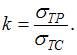 Для хрупкого материала  где  – предел прочности материала при растяжении,  – предел прочности материала при сжатии.

83. Площадки в исследуемой точке напряженного тела, на которых касательные напряжения равны нулю, называют главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями.

84. Напряженное состояние при значениях , , 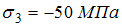называют плоским.

85. Три взаимно перпендикулярные оси, в системе которых отсутствуют угловые деформации, называют главными осями деформированного состояния. Среди множества осей, проходящих через точку, в которой исследуется деформированное состояние, существуют три взаимно перпендикулярные оси, в системе которых угловые деформации равны нулю. Эти оси называются главными осями деформированного состояния, а линейные деформации в этой системе – главными деформациями.

86. Совокупность линейных и угловых деформаций, возникающих по раз-личным осям и в различных плоскостях, проходящих через данную точку тела, называют деформированным состоянием в точке.

В общем случае элементарный объем испытывает три линейные деформации и три угловые. Деформированное состояние в точке полностью определяется, если заданы шесть компонентов тензора деформаций (  ,  ,  ,  ,  ,  ). Зная эти компоненты, можно определить линейную и угловую деформации в любом направлении и в любой плоскости, проходящей через данную точку. Совокупность этих деформаций по множеству направлений и плоскостей, проходящих через данную точку, и называется деформированным состоянием в этой точке.

87. Модуль упругости материала E и коэффициент Пуассона M заданы. Относительное изменение объёма равно

88. Главные напряжения для напряженного состояния, показанного на рисунке, равны