4.2. Элементарные функции
В таблице 4.2 приведен перечень известных из школьного курса функций и их графиков. Эти функции называются основными элементарными функциями.
Элементарными функциями называются функции, которые можно получить из основных элементарных функций (перечисленных в таблице) с помощью алгебраических операций и композиций функций.
Примеры:
______________________________________________________________________________
Функция
у
= 
+ 
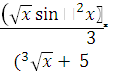является элементарной, так как она получена с помощью операций сложения, вычитания, умножения, деления и образования сложной функции.
Функция у = |x| (рис. 4.4) я
вляется
примером неэлементарной функции
у
y
= |x|
х
Рис. 4.4
________________________________________________________________
Таблица 4.2
|
Аналитическое задание |
Область определения Х |
Область значений Y |
График |
Степенная функция
|
у = xⁿ , n
у = x⁻ⁿ , n
y= n
n
|
(-
(-
(-
(-
если nнечетно;
|
(-
Если nнечетно; , еслиnчетно
(-
(-
(-
если nнечетно;
|
0 1 х 0 1 х
у = |
N
N
,
N,
1
,
+
)
,
0)
,
+
)
,
+
),
,
еслиnчетно
,
+
),
,
0)
,
+
),
еслиnнечетно;
,
еслиnчетно
,
+
),
,
еслиnчетно
у у
y=
1
у = х
у у
у = 1/xу
=1/ х?
0 1x0 1x
у у
у =
0
1 х 0 1 х2.Показательная функция
|
у =
а
а |
(- |
|
y
= 0
1 a
|
,
0,
1
,
+ 
)
y
a 
1 
1
0 1 x
|
Аналитическое задание |
Область определения Х |
Область значений Y |
График |
3.Логарифмическая функция
|
y= a a |
( |
(- |
a > 1
y =
0 1 x
0 < a < 1
|
₁
0,
1
,
+ 
)
Y
4.Тригонометрические функции
|
y=sinx
У |
(-
(- |
[-1,1]
[-1,1] |
у
1 - -1
1
-п -
|
= сosx
,
+ 
)
,
+ 
)
0
2П
-П П/2 П 2П х
y
0
п х
-1
|
y= tg x |
(- N |
(- |
-п
- |
+ Пn,
+ Пn),
Z
,
+ 
)
y
0
П x