208 Чел.

По чертежу видно, что для ответа на вопрос задачи, надо к 156 прибавить 208.

Обучение решению составных задач

Часто при решении задачи для того, чтобы найти ответ на вопрос, нужно выполнить несколько действий. Такие задачи называют составными. Решение составной задачи сводится к последовательному решению простых задач. Для этого надо установить ряд связей между данными и искомыми, выбрать, а затем выполнить необходимые арифметические действия.

При подготовке к введению составных задач учащиеся должны уяснить, чем составная задача отличается от простой – ее нельзя решить одним действием.

В качестве подготовительной работы можно предложить ряд упражнений. Например, решение простых задач с недостающими данными. Учитель предлагает задачу: «К концу игры на шашечной доске остались чёрные и 3 белые шашки. Сколько шашек осталось на доске?». Анализируя задачу, дети выясняют, что ответить на вопрос задачи мы не можем, т.к. не знаем, сколько черных шашек осталось на доске. Дети дополняют недостающие данные и решают задачу. При выполнении такого задания дети приходят к вводу, что на вопрос задачи можно ответить не всегда, т.к. может не хватать данных. Для того чтобы ответить на вопрос задачи, эти данные надо добавить в условие задачи.

Полезным будет также решение простых задач, в которых ответ на вопрос одной задачи является одним из данных второй задачи, например: «Костя надул 9 воздушных шариков, а Стёпа в 2 раза больше, чем Костя. Сколько воздушных шариков надул Стёпа?» и вторая задача: «Костя надул 9 воздушных шариков, а Стёпа 18 шариков. Сколько воздушных шариков надули мальчики?». Учитель формулирует новую задачу, которая заменяет две предыдущие: «Костя надул 9 воздушных шариков, а Стёпа в 2 раза больше, чем Костя. Сколько воздушных шариков надули мальчики?». Для того чтобы решить эту задачу, нужно вначале решить первую из данных задач, а затем – вторую. В дальнейшем дети самостоятельно будут заменять пары простых задач одной составной.

Также в одной и той же задаче к условию могут быть сформулированы 2 вопроса, например: «Катя знает 10 сказок, а Маша – на 2 сказки больше. Сколько сказок знает Маша? Сколько сказок знают обе девочки? (283, 1 класс)

Еще одно задание – формулировка вопроса по данному условию. Пусть дано условие: «На 8 тарелок положили по 3 апельсина»; нужно сформулировать, что можно найти по этим данным.

Наиболее удачными для ведения составных задач являются задачи, включающие в себя 2 простые задачи на нахождение суммы и разности, например: «В вазе лежало 5 яблок и 4 груши. 2 фрукта съели. Сколько фруктов осталось в вазе?». При разборе задачи учитель спрашивает, что известно о фруктах, лежавших в вазе и записывает условие кратко. (Было 5 яблок и 4 груши.) Что еще известно в условии задачи? (Съели 2 фрукта.) Что надо узнать? (Сколько фруктов осталось?) На доске параллельно с разбором задачи появляется краткая запись:

Было – 5 яб. и 4 гр.

Съели – 6 фр.

Осталось – ?

Далее учитель просит детей по краткой записи объяснить, что обозначает каждое из чисел в условии задачи, и что требуется найти.

Для объяснения решения задачи воспользуемся предметной наглядностью. Берем изображения 5 яблок и 4 груш и кладем их в вазу. Затем достаем 2 любых фрукта и откладываем их в сторону. Оставшиеся фрукты должны лежать, чтобы их число нельзя было найти пересчетом. Учитель спрашивает, можно ли сразу найти число оставшихся фруктов? (Нет, мы не знаем, сколько фруктов лежало в вазе.) А можем ли мы узнать, сколько фруктов лежало в вазе? (Можем, надо к 5 прибавить 4.) Записываем это действие на доске: 5 + 4 = 9 (фр.) – было в вазе. Можно ли теперь узнать, сколько фруктов осталось в вазе? (Да, надо из 9 вычесть 2.) Записываем второе действие: 9 – 2 = 7 (фр.)

Работа над другими составными задачами ведется примерно по такому же плану. Поскольку видов составных задач достаточно много, то важно научить младших школьников общим приемам работы над задачей, т.е. дети должны научиться самостоятельно анализировать задачу, устанавливать связи между данными и искомыми, выполнять необходимые иллюстрации к задаче, составлять план решения, реализовывать этот план, записывая выполняемые действия, проверять, правильно ли решена задача.

Для того чтобы этот план работы над задачей был усвоен детьми, можно составить и выдать каждому ребенку памятку как работать над задачей. В дальнейшем такая система работа над задачей будет применяться детьми для работой над задачами новых типов.

Задачи в два действия на сложение и вычитание по степени сложности можно разделить на группы. К первой группе можно отнести задачи с тремя данными, в которых промежуточное действие и действие, отвечающее на вопрос задачи, относятся к разным предметам, при этом действия над этими предметами могут быть как одинаковыми, так и различными. Например: «На полке стояли книги: 6 сборников сказок и 4 фантастические повести. Ника прочитала 3 книги. Сколько книг осталось прочитать Нике?» (327, 1 класс)

Ко второй группе относятся задачи с двумя данными, а действия в промежуточном и основном вопросе различны: «Нина разгадала в кроссворде 12 слов, а Люба на 2 слова меньше. Сколько слов разгадали девочки в кроссворде?» (299, 1 класс)

Третья группа – это задачи с двумя данными и одинаковыми действиями в промежуточном и основном вопросах. При этом действия относятся к одним и тем же предметам: «Корова кота Матроскина Мурка утром даёт 9 л молока, а вечером – на 4 л больше. Сколько литров молока даёт Мурка за сутки?» (301, 1 класс)

Знакомя детей с составными задачами, можно придерживаться приведенной выше последовательности.

Рассмотрим более подробно решение каждого вида составных задач.

Составные задачи на нахождение суммы

Задачи такого вида – это, как правило, первые составные задачи, с которыми сталкиваются дети. До этого дети долгое время решали простые задачи, в которых по двум данным числам надо было найти третье число. Дети привыкли вычленять из условия задачи данные числа и оперировать ими. В результате выполненного действия они сразу получали ответ на требование задачи. Таким же образом они зачастую поступают и при решении составных задач. Например, дана задача: «Катя знает 10 сказок, а Маша – на 2 сказки больше. Сколько сказок знают обе девочки?» (283, 1 класс) Ребенок рассуждает так: надо узнать, сколько сказок знают обе девочки, значит, задача решается действие сложения; в задаче есть числа 10 и 2, значит, чтобы узнать, сколько сказок знают обе девочки, надо к 10 прибавить 2, получим 12 сказок. Или другая ошибка: в задаче сказано, что Маша знает на 2 сказки больше, выбираем действие сложения: 10 + 2 = 12 (сказок). Также при решении первых составных задач ребенок может устно найти результат первого действия и записать только второе действие: 10 + 8 = 18 (сказок).

Чтобы предупредить такие ошибки, можно, например, на уроке предложить одновременно две задачи: «Буратино правильно решил 9 примеров, а Незнайка – на 3 примера меньше. Сколько всего примеров решил Незнайка?», «Буратино правильно решил 9 примеров, а Незнайка – 6 примеров. Сколько всего примеров решили Буратино и Незнайка?». Задачи таких типов детям к моменту знакомства с составной задачей уже хорошо знакомы и не должны вызывать затруднений. Затем после решения данных задач формулируются составная задача: «Буратино правильно решил 9 примеров, а Незнайка – на 3 примера меньше. Сколько всего примеров решили Буратино и Незнайка?». (293, 1 класс) Обсуждая решение первой и второй задач, мы приходим к выводу, что решив их, мы нашли ответ на требование последней задачи, поэтому ее решение можно записать при помощи выражения: 9 + (9 – 3). Т.е. для того, чтобы ответить на вопрос задачи, нужно выполнить два действия.

Составные задачи на нахождение суммы можно в свою очередь можно разбить на типы, например: нахождение суммы трех слагаемых; нахождение суммы двух слагаемых, одно из которых дано в условии задачи, а про второе известно, что оно больше или меньше другого на несколько единиц или в несколько раз; нахождение суммы трех слагаемых, одно из которых дано в условии задачи, второе – больше или меньше другого на несколько единиц или в несколько раз, а третье равно, например, сумме первого и второго слагаемых и др.

Рассмотрим задачу: «Почтальон Печкин принёс жителям Простоквашино 8 газет, 4 журнала и 2 телеграммы. Сколько всего газет, журналов и телеграмм принёс в Простоквашино почтальон?» (282, 1 класс) Несмотря на то, что в задаче даны 3 числа, и она является составной, задача от простых задач на нахождение суммы отличается незначительно. Отличием будет то, что требуется найти сумму не двух, а сразу трех слагаемых. Решение таких задач можно записывать при помощи выражения: 8 + 4 + 2 = 14 (шт.) Трудность в оформлении этой задачи состоит в том, что не очень понятно, что записать в скобках, т.е. каким одним словом назвать газеты, журналы и телеграммы. Что касается решения задачи, то особых трудностей она вызвать не должна, но в случае необходимости можно использовать графическую модель, причем данные на чертеж дети могут внести самостоятельно.

Рассмотрим еще оду задачу: «На деревьях в роще грачи свили гнёзда. На берёзах 12 гнёзд, а на липах на 8 гнёзд больше. Сколько всего гнёзд свили грачи в роще?» (295, 1 класс)

Прочитав задачу, учитель просит детей выделить в ней условие, вопрос, наиболее важные слова и числа.

Т.к. задача содержит более двух данных, полезным будет составить краткую запись задачи. Это позволит воспринять всю задачу целиком, а не выискивать каждый раз в условии задачи необходимые данные. Краткая запись может быть такой:

Б. – 12 гн.

Л. – ?, на 8 гн. больше

В краткой записи мы поставили два знака вопроса, значит, задача будет решаться двумя действиями. Главный вопрос задачи можно обвести в кружочек, это поможет детям сориентироваться при разборе задаче в порядке выполнения действий.

Эту запись ученики могут прокомментировать так: «На березах 12 гнезд; сколько гнезд на липах неизвестно, но мы знаем, что их на 8 больше, чем на березах. Фигурная скобка и знак вопроса указывают, что нужно найти, сколько гнезд на деревьях всего, – это основной вопрос задачи».

Анализ задачи можно провести при помощи следующих вопросов: что известно в задаче; что нужно найти; можем ли мы сразу ответить на вопрос задачи; что нужно знать, чтобы ответить на вопрос задачи; можем ли мы узнать, сколько гнёзд было свито на липах; каким действием мы можем это найти; можем ли мы ответить на вопрос задачи, зная число гнёзд на березах и число гнеёд на липах; каким действием мы можем это сделать?

Существенную помощь при решении такой задачи может оказать графическая модель:

Б

12 гн.

8 гн.

.

Л.

Особенно схемы могут помочь при решении задач, в которых есть слова «столько же», например: «Саша нашёл 5 белых грибов, 6 подберёзовиков и столько же лисичек. Сколько всего грибов нашёл Саша?» (285, 1 класс) Сложность при решении задачи состоит в том, что не указано число лисичек, поэтому это условие задачи дети могут пропустить. При анализе задачи выясняем, какие грибы нашел Саша, и чертим друг за другом 3 отрезка. Т.к. в условии задачи сказано, что лисичек столько же, сколько и подберезовиков, указываем на чертеже число лисичек. По чертежу становится видно, что для того, чтобы найти ответ на вопрос задачи, надо сложить 3 числа; записываем решение задачи: 5 + 6 + 6 = 17 (гр.).

Составные задачи на нахождение остатка

При решении составных задач на нахождение остатка следует обратить внимание на то, что многие задачи можно решить несколькими способами. Рассмотрим задачу: «В море ушли 20 больших рыбацких лодок и 8 маленьких. 6 больших и 3 маленьких лодки вернулись в порт. Сколько лодок должны ещё вернуться?» (352, 1 класс)

Первый способ.

1. Сколько лодок ушло в море? 20 + 8 = 28 (л.)

2. Сколько лодок вернулось? 6 + 3 = 9 (л.)

3. Сколько лодок должны еще вернуться? 28 – 9 = 19 (л.)

Второй способ.

1. Сколько должно вернуться больших лодок? 20 – 6 = 14 (л)

2. Сколько должно вернуться маленьких лодок? 8 – 3 = 5 (л.)

3. Сколько всего лодок должны вернуться? 14 + 5 = 19 (л.)

Третий способ.

1. Сколько лодок ушло в море? 20 + 8 = 28 (л.)

2. Сколько лодок должно вернуться после возвращения больших лодок? 28 – 6 = 22 (л.)

3. Сколько всего лодок должны вернуться? 22 – 3 = 19 (л.)

В случае если задачи такого типа вызывают у детей затруднение, можно проиллюстрировать условие задачи с помощью графической модели. Рассмотрим задачу: «В саду доброй волшебницы распустилось 30 прекрасных цветов. 9 она подарила бедной девушке, а 7 – мудрой женщине. Сколько цветов осталось в саду доброй волшебницы?» (360, 1 класс)

Построим графическую модель:

30

9

7

?

Работа над составными задачами на нахождение неизвестного, на нахождение третьего слагаемого, уменьшаемого, задачи на разностное сравнение и др. ведется аналогично.

Составные задачи на нахождение третьего слагаемого

Рассмотрим задачу: «Верблюд под палящими лучами солнца проходит за день 90 км. До первой стоянки верблюд прошёл 38 км, до второй – на 2 км больше. Сколько километров ему осталось пройти до последней стоянки?» (78, 3 класс)

Удобно проиллюстрировать задачу с помощью графической модели:

90 км

?

38 км

38 + 2

По схеме видно, что известна сумма, одно из слагаемых, также становится понятным, как найти второе слагаемое. Поскольку в задаче сказано, что во второй день верблюд проходит на 2 км больше, то на схеме длину пройденного во второй день пути запишем в виде выражения; это облегчит дальнейшее решение задачи.

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. У нас слагаемых два, поэтому, чтобы его найти, можно из суммы вычесть сумму первого и второго слагаемых, а можно из суммы вычесть первое слагаемое, а затем из полученного результата вычесть второе слагаемое.

Таким образом, задачу можно решить двумя способами.

Первый способ.

1. 38 + 2 = 40 (км) – прошел верблюд во второй день;

2. 38 + 40 = 78 (км) – прошел верблюд за 2 дня;

3. 90 – 78 = 12 (км) – прошел верблюд за третий день.

Решая задачу другим способом, вторым действием найдем, сколько километров останется пройти верблюду после первого дня пути.

Поиск различных способов решения задачи полезно, т.к. в этом случае дети не запоминают способ решения конкретного типа задачи, а ищут различные способы решения задачи, овладевают общими умениями анализировать задачу.

Задачи на нахождение четвертого пропорционального

Решение такого вида задач основывается на знании связей между величинами, например, чтобы найти производительность труда, надо объем работы разделить на время и т.д. Следовательно, подготовительная работа к решению такого рода задач должна предусматривать знакомство с этими величинами и раскрытие связей между этими величинами. При этом можно детям предложит ряд простых задач, на основе которых учащиеся усваивают способ нахождения одной из величин.

В задачи такого вида входят три пропорциональных величины, например, цена, количество, стоимость; скорость, время, расстояние; производительность труда, время работы, объем работы и др. В большинстве таких задач для одной величины даны два значения, например, производительность труда одного и другого рабочего, другая величина, например, время работы постоянна, дано значение объема работы одного рабочего, требуется найти значение объема работы другого рабочего.

Используя любые три пропорциональные величины, можно составить шесть видов задач на четвертое пропорциональное. Любую из этих задач можно решить, найдя значение постоянной величины.

Рассмотрим работу над задачами такого типа на следующем примере: «В магазин привезли 36 кг апельсинов и разложили поровну в 6 пакетов. Сколько потребуется пакетов, чтобы разложить 54 кг апельсинов?» (416, 3 класс)

Краткую запись к задаче удобнее всего сделать в виде таблице:

Масса одного пакета	Количество пакетов	Масса апельсинов (кг)
одинаковая	6	36
	?	54

На начальном этапе работы над задачей дети объясняют, что показывает каждое число. Перед решением задачи можно сделать прикидку результата. В нашей задаче во втором случае апельсинов больше, а пакеты одинаковые, поэтому пакетов во втором случае получится больше.

Дети вместе с учителем выясняют, что для того чтобы найти количество пакетов во втором случае, надо знать массу одного пакета. А массу одного пакета можно найти из первой строчки, т.к. мы знаем массу всех апельсинов и количество пакетов. Массу одного пакета можно найти действием деления. А зная массу одного пакета и массу всех апельсинов, мы сможем количество пакетов.

Проверить решение задачи можно, составив и решив обратную задачу.

Особо можно выделить задачи на нахождение четвертого пропорционального, при решении которых используются свойства прямой или обратной пропорциональности. Рассмотрим задачу: «На рынке 2 кг ягод стоят 150 руб. Сколько стоят 10 кг ягод?» (639, 4 класс) Задачу можно решить так же, как и предыдущую задачу: первым действием найти цену ягод, а вторым ответить на вопрос задачи, а можно решить по-другому. Цена ягод и их стоимость находятся в прямо пропорциональной зависимости: во сколько раз больше будет куплено ягод, во столько же раз придется заплатить больше денег. Тогда первым действием можно будет узнать, во сколько раз во втором случае купили больше ягод: 10 : 2 = 5 (раз). Т.к. ягод купили в 5 раз больше, то и денег за ягоды придется заплатить в 5 раз больше: 150 · 5 = 750 (руб.). Следует отметить, что встречаются задачи, которые можно решить лишь одним из указанных способов, это зависит от того, можно ли найти частное данных в задаче чисел. Например, если в предыдущей задаче поменять данные: то её можно решить только первым способом. А если задачу сформулировать так: «На рынке 2 кг ягод стоят 115 руб. Сколько стоят 10 кг ягод?», то задача решается только вторым способом. Если есть такая возможность то будет полезным рассмотреть оба способа решения задачи.

Второй способ решения задачи на нахождение четвертого пропорционального будет также являться подготовкой к решению задач на тройное правило. Рассмотрим задачу: «Три курицы за 3 дня снесут 3 яйца. Сколько яиц снесут 6 куриц за 6 дней?» (699, 4 класс) условие задачи сформулировано таким образом, что прочитав задачу, дети часто сразу дают ответ 6, он является неверным. Рассуждения при решении задачи могут быть такими: кур стало в 2 раза больше, значит и яиц они снесут в 2 раза больше; дней стало в 2 больше, значит, яиц также будет в 2 раза больше. Запишем решение задачи: 3 · 2 · 2 = 12 (яиц).

Следующая задача: «Три кошки съедают 3 мышек за 1 ч 30 мин. За какое время 10 кошек съедят 20 мышек?» (713, 4 класс). Здесь рассуждения будут сложнее, т.к. 10 на 3 не делится, кроме этого время выражено в часах и минутах. Рассуждать будем так: т.к. три кошки съедают 3 мышек за 1 ч 30 мин, то это значит, что каждая кошка за это время съела по одной мышке. Во втором случае 10 кошек съедают 20 мышек, т.е. каждая кошка съедает по 2 мышки, т.е. в 2 раза больше, чем в предыдущем случае, значит, и времени на это каждой кошки потребуется в 2 раза больше: 1 ч 30 мин · 2 = 3 ч.

Задачи на нахождение неизвестного по двум разностям

Такого рода задачи содержат два значения одной переменной и разность соответствующих значений другой переменной. Требуется найти значения этой переменной. Например, известны скорости двух движущихся объектов и разность пройденного расстояния при постоянном времени или известны разность цен и стоимость покупок при постоянном количестве купленных покупок.

При решении задач такого вида применяется способ нахождения постоянной величины.

При введении задач такого вида можно воспользоваться предметной иллюстрацией.

Рассмотрим задачу: «Одна девочка купила 4 общие тетради, другая – 6 таких же тетрадей и заплатила за свою покупку на 48 руб. больше, чем первая. Сколько заплатила каждая девочка за тетради?» (197, 4 класс)

На одну полку выложим 4 тетради, а на другую – 6 тетрадей. При работе над задачей дети должны понять, что другая девочка купила столько тетрадей, сколько первая девочка и еще 2 тетради и заплатила за все тетради столько же денег, сколько первая девочка и еще 48 рублей. Из этого можно сделать вывод, что 48 руб. стоят 2 тетради, значит одна тетрадь стоит 48 : 2 = 24 (руб.)

Краткую запись условия задачи удобно записывать в виде таблицы:

	Цена (руб.)	Количество (тетр.)	Стоимость (руб.)
Первая девочка	одинаковая	4	?
Вторая девочка		6	?, на 48 руб. больше

На первом этапе ознакомления с задачами такого вида можно предлагать задачи не в готовом виде, а составлять задачи из задач на нахождение четвертого пропорционального.

Рассмотрим задачу: «Один огородник приготовил для посадки 2 пакета лука-севка, а другой – 5 таких же пакетов. У второго огородника получилось на 15 кг лука. Сколько килограммов лука приготовил для посева первый огородник?».

Внесем данные задачи в таблицу:

	Масса пакета (кг)	Количество (пак.)	Масса лука (кг)
Первый огородник	одинаковая	2	?
Второй огородник		5	15

Детям такие задачи уже знакомы. Первым действием находим массу одного пакета: 15 : 5 = 3 (кг); вторым действием находим массу лука, который заготовил первый огородник: 3 2 = 6 (кг). После этого дети находят разность чисел, показывающих массу лука, заготовленного первым и вторым огородником. Записываем найденное значение в таблицу:

	Масса пакета (кг)	Количество (пак.)	Масса лука (кг)
Первый огородник	одинаковая	2	?
Второй огородник		5	?, на 9 кг больше

Получили новую задачу: «Один огородник приготовил для посадки 2 пакета лука-севка, а другой – 5 таких же пакетов. У второго огородника получилось на 9 кг лука больше, чем у первого. Сколько килограммов лука приготовил для посева каждый огородник?» (203, 4 класс)

Существенную помощь при решении задачи может оказать схема с отрезками.

I

II

9 кг

При составлении схемы выясняется, что 9 кг лука второго огородника находятся в трех пакетах. Пользуясь чертежом, составить план решения задачи становится не столь сложным. Первым действием находим, на сколько пакетов лука у второго огородника было больше: 5 – 2 = 3 (пакета). Вторым действием можно найти, сколько килограммов лука находится в одном пакете: 9 : 3 = 3 (кг). Тогда третьим и четвертым действием можно ответить на вопрос задачи: 3 2 = 6 (кг) лука заготовил первый огородник; 35 = 15 (кг) лука заготовил второй огородник.

Для того чтобы проверить правильность решения задачи, можно установить соответствие между данными и полученными числами, т.е. найти разницу заготовленного каждым огородником лука: 15 – 6 = 9 (кг). Полученное число соответствует условию, значит, задача решена верно.

Задачи на пропорциональное деление

Для того чтобы дети легко справились с решением задач на пропорциональное деление, к моменту введения задач этого типа ими хорошо должны быть усвоено решение задач на нахождение четвертого пропорционального.

При введении такого типа задач лучше всего составлять их вместе с детьми из задач на четвертое пропорциональное, а не давать в готовом виде. Например, рассмотрим задачу: «В 12 палатах 72 койки. Сколько коек в 9 таких же палатах?» (430, 3 класс)

Запишем условие задачи кратко:

Число коек в одной палате	Количество палат	Число коек
одинаковое	12	72
	9	?

Решив задачу, дети узнают, что в 9 палатах 54 койки и затем находят, сколько всего коек во всех палатах. Их 126. После этого учитель вносит полученное число в таблицу, а число коек в 12 палатах заменяет знаком вопроса:

Число коек в одной палате	Количество палат	Число коек
одинаковое	12	? 126 ?
	9

По данной таблице дети составляют новую задачу: «В больнице на одном этаже 12 палат, а на втором – 9 таких же палат. Всего в этих палатах 126 коек. Сколько коек на первом этаже и сколько – на втором?». Учитель просит детей заменить два вопроса одним. Тогда задача примет такой вид: «В больнице на одном этаже 12 палат, а на втором – 9 таких же палат. Всего в этих палатах 126 коек. Сколько коек на каждом этаже?».

При анализе задачи учитель может задать детям следующие вопросы: что требуется узнать в задаче? Можно ли сразу узнать, сколько коек было в 12 палатах или сколько коек было в 9 палатах? Что для этого нужно знать? (Число коек в одной палате). Можем ли мы сразу узнать, сколько коек было в одной палате? (Нет). Что для этого необходимо знать? (Общее число палат.) После проведенного анализа записывается решение задачи по действиям.

Рассмотрим готовую задачу на пропорциональное деление: «В одной школе 22 класса, в другой – 18. В школы завезли 1600 учебников математики. Сколько учебников выдали учащимся каждой школы, если их выдавали поровну всем классам?» (223, 4 класс) Прежде чем приступить к разбору задачи, необходимо выяснить, как дети понимают, что значит «учебники выдали учащимся каждой школы», а затем переформулировать задачу так, чтобы в ней было два вопроса: «Сколько учебников выдали ученика первой школы и сколько учебников выдали ученикам второй школы?»

Запишем условие задачи кратко:

Число учебников для одного класса	Количество классов	Количество учебников
одинаковое	22	? 1600 ?
	18

Затем составляем план решения задачи, рассуждая от вопроса: первым действием узнаем количество классов в двух школах; вторым действием – количество учебников для одного класса; третьим – количество учебников для одной школы и четвертым – количество учебников для второй школы. Чтобы проверить правильность решения задачи, можно сложить полученные значения и сравнить результат количеством учебников, данных в условии задачи.

Другой тип задач на пропорциональное деление: «Кондитерская фабрика выпустила в первый день 336 кг печенья, а во второй – 408 кг. Всего за два дня она выпустила 62 одинаковых ящика печенья. Сколько ящиков печенья выпускала фабрика каждый день?» (221, 4 класс). В этой задаче в отличие от предыдущей известно общее количество ящиков печенья, т.е. в отличие от предыдущей задачи при нахождении массы одного ящика нам известен делитель, а делимое находится действием сложения.

В качестве дополнительной работы над задачей можно предложить детям задания на преобразования задач, например, после решения задачи на четвертое пропорциональное можно составить задачи на нахождение неизвестных по двум разностям или сформулировать и решить задачу на пропорциональное деление, а затем найти сходства и отличия в решении этих задач.

Задачи на встречное движение и движение в противоположных направлениях

Подготовительной работой к решению задач на движение является решение простых задач на нахождение скорости, времени и расстояния. При решении такого типа задач дети должны усвоить понятие скорости, а также установить связи между этими величинами, запомнить правила нахождения неизвестной величины.

Наблюдая за движущимися объектами, дети вместе с учителем выясняют, как могут двигаться два тела: они могут двигаться навстречу друг другу, при этом они будут сближаться; также тела могут двигаться в разные стороны, удаляясь друг от друга; кроме этого они могут двигаться в одном направлении, при этом они могут сближаться или удаляться друг от друга. Разные варианты движения можно обсудить с детьми, используя подвижную наглядность.

Можно выделить следующие типы задач: известны скорости каждого из движущихся тел и время движения, требуется найти пройденное расстояние; даны скорости каждого из тел и расстояние, требуется найти время движения; известны расстояние, время движения и скорость одного из движущихся тел, требуется найти скорость другого тела.

Первые задачи, с которыми встречаются дети – это задачи на встречное движение, когда тела начинают двигаться одновременно. Важно, чтобы дети хорошо усвоили, что если тела вышли навстречу друг другу одновременно, то до момента встречи они будут находиться в пути одинаковое время. Что касается расстояния, то следует отметить, что оба тела за отведенное время проехали все расстояние. Для того чтобы эти факты были усвоены детьми, можно предложить, например, такие вопросы: «Два пешехода вышли одновременно из двух пунктов и встретились через полчаса. Сколько времени был в пути каждый пешеход?».

Необходимым условием для успешного решения задачи на движение является выполнение чертежа. Первые чертежи дети выполняют под руководством учителя, при этом учитель показывает, что расстояние обозначается отрезком, пункты отправления – точками и соответствующими буквами, а направление движения – стрелками. Также на чертеже можно указать скорости движения тел, время, которое они были в пути, пройденные ими расстояния, а место встречи обозначить флажком.

Р

30 с

ассмотрим чертеж, который можно выполнить к задаче: «Расстояние между двумя велосипедистами было 240 м. Они выехали одновременно навстречу друг другу и встретились через 30 с. Найди скорость первого велосипедиста, если скорость второго была равна 3 м/с.» (296, 4 класс)

240 км

3 м/с

?

Подготовкой к решению задач на встречное движение могут служить такие задачи, как: «Навстречу друг другу из двух сел, расстояние между которыми 30 км одновременно вышли два пешехода. Один шел со скоростью 4 км/ч, а другой – со скоростью 5 км/ч. На сколько километров они сблизятся за 1 ч пути? За 3 ч пути?»

Дети выполняют к каждой задаче чертеж:

30 км

4 км/ч

1 ч

1 ч

5 км/ч?

30 км

4 км/ч

5 км/ч?

3 ч

3 ч

При решении задач дети под руководством учителя выясняют, что ответ на первый вопрос задачи (за 1 ч пешеходы сблизились на 9 км) смог помочь им ответить на второй вопрос задачи. Причем ответ на второй вопрос задачи мы можем найти двумя способами: 4 3 + 53 или (4 + 5)3. После этого можно ввести понятие скорости сближения: скоростью сближения называют расстояние, на которое сближаются движущиеся объекты за единицу времени.

Другой тип подготовительных задач – это задачи, в которых известно первоначальное расстояние или расстояние, которое осталось пройти до встречи движущимся телам, а также пройденное расстояние того и другого движущегося объекта. Например: «Два автомобиля выехали одновременно навстречу друг другу из двух городов, расстояние между которыми 120 км. Один автомобиль проехал 40 км, а другой – 50 км. На каком расстоянии друг от друга находятся автомобили?» или другая задача: «Два автомобиля выехали одновременно навстречу друг другу из двух городов. После того как один автомобиль проехал 40 км, а другой – 50 км, между ними осталось 120 км. Найдите расстояние между городами.»

Задачи на встречное движение разных видов можно ввести одновременно, причем начинать лучше с задачи, в которой известны скорости обоих тел и время их движения, например: «Из двух сел одновременно навстречу друг другу выехали два велосипедиста. Скорость одного велосипедиста 13 км/ч, другого – 11 км/ч. Найдите расстояние между селами, если велосипедисты встретились через 4 часа.»

Учитель инсценирует задачу при помощи двух учеников или может воспользоваться подвижной наглядностью. На чертеже можно отметить расстояния, которые проезжали велосипедисты за каждый час пути.

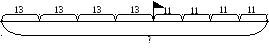
Пользуясь полученным чертежом, ученики без труда смогут найти два способа решения задачи.

Первый способ.

1. 13 4 = 52 (км) – проехал первый велосипедист;

2. 11 4 = 44 (км) – проехал второй велосипедист;

3. 52 + 44 = 96 (км) – расстояние между селами.

После этого дети под руководством учителя находят второй способ решения задачи. Для этого можно спросить у школьников, что произойдет через час, через два часа после начала движения (велосипедисты сблизятся на 24 км; после того, как пройдет еще один час, велосипедисты сблизятся еще на 24 км).

Дети под руководством учителя выполняют чертеж:

13 км/ч

11 км/ч

4 ч

?

При выполнении чертежа следует отметить, что первый велосипедист едет с большей скоростью, поэтому он до встречи проедет большее расстояние. Следовательно, флажок поставим ближе к месту отправления второго велосипедиста.

Получаем второй способ решения задачи:

1. 13 + 11 = 24 (км/ч) – скорость сближения велосипедистов;

2. 24 4 = 96 (км) – расстояние между селами.

После решения задачи вторым способом можно изменить чертеж к задаче (это можно сделать как на данном уроке, так и на следующем):

96 км

13 км/ч

11 км/ч

?

Учитель просит детей составить по этому чертежу задачу, а затем ее решить (после коллективного разбора).

Для данного типа задачи на встречное движение существует только один способ решения:

1. 13 + 11 = 24 (км/ч) – скорость сближения велосипедистов;

2. 96 : 24 = 4 (ч) – был в пути до встречи каждый велосипедист.

Для данной задачи можно составить еще две обратные. Рассмотрим одну из них.

В отличие от предыдущей данная задача имеет два способа решения.

Первый способ.

1. 13 4 = 52 (км) – проехал до встречи первый велосипедист;

2. 96 – 52 = 44 (км) – проехал до встречи второй велосипедист;

3. 44 : 11 = 11 (км/ч) – скорость второго велосипедиста.

Второй способ.

1. 96 : 4 = 24 (км/ч) – скорость сближения велосипедистов;

2. 24 – 13 = 11 (км/ч) – скорость второго велосипедиста.

В дальнейшем при решении задач на встречное движение необходимо включать задачи разных видов в готовом виде, при этом дети должны выполнять чертеж самостоятельно. Следует отметить, что при решении задач на встречное движение выполнение чертежа является необходимым условием успешного решения задачи.

Рассмотрим еще одну задачу: «Со станции одновременно в разных направлениях отправились два поезда. Скорость одного поезда 43 км/ч, другого – 56 км/ч. Какое расстояние будет между ними через 5 ч? (302, 4 класс) Отличие этой задачи от предыдущих состоит лишь в том, что поезда движутся в противоположных направлениях и из одной точки.

43 км/ч

56 км/ч

5 ч

5 ч

?

По чертежу хорошо видно, что для того чтобы найти расстояние, которое будет между поездами через 5 ч, можно сложить расстояния, которые прошли поезда за 5 ч в отдельности. Другой способ решения задачи заключается в том, что вначале можно найти, какое расстояние будет между поездами через 1 час, т.е. скорость удаления, а затем результат умножить на 5.

В первом случае для решения задачи можно составить выражение 43 5 + 565, а во втором – (43 + 56)5.

Более сложными для понимания младшими школьниками являются задачи на движение в одном направлении, например: «Из города одновременно в одном направлении выехали грузовая и легковая машины. Скорость грузовой машины 73 км/ч, а скорость легковой машины 88 км/ч. Какое расстояние будет между ними через 6 ч?» (306, 4 класс)

Также как и в предыдущих случаях, необходимо выполнить к задаче чертеж. Если при движении в противоположных направлениях участники движения проезжали или проходили разные участки пути, то при движении в одном направлении они идут или едут по одной и той же дороге. Чтобы чертеж был нагляднее, можно все данные первого участника движения записывать сверху от изображенного отрезка, а второго – снизу от него.

? км

73 км/ч

6 ч

6 ч

88 км/ч

По чертежу видно, что скорость легковой машины больше, поэтому за 6 ч она проедет большее расстояние, надо узнать, на сколько больше.

Задача также может быть решена двумя способами.

Первый способ.

1. 73 6 = 438 (км) проехала грузовая машина;

2. 88 6 = 528 (км) – проехала легковая машина;

3. 528 – 438 = 90 (км) – будет между машинами через 6 ч.

Второй способ.

1. 88 – 73 = 15 (км/ч) – скорость удаления;

2. 15 6 = 90 (км).

Преимущество первого способа состоит в том, что он проще для понимания, второго – короче и содержит меньше вычислений.

Рассмотрим еще несколько задач на движение, более сложных, чем предыдущие. Задача: «Ну, заяц, погоди!» – зарычал волк и бросился за зайцем. Каждый шаг зайца был в 2 раза короче шага волка, но заяц делал шаги в три раза чаще, чем волк. Догонит ли волк зайца?» (637, 3 класс) Выразим скорости зайца и волка в шагах зайца. В то время как волк делает шаг, т.е. 2 заячьих шага, заяц успевает сделать три шага. Получается, что заяц удаляется от волка, и каково бы ни было расстояние между ними в начальный момент времени, волк зайца догнать не сможет.

Еще одна интересная задача: «Два велосипедиста выехали навстречу друг другу из пунктов, находящихся друг от друга на расстоянии 20 км. Скорость каждого велосипедиста 10 км/ч. Одновременно вместе с первым выбежала собака. Собака бегала между велосипедистами: добежав до второго, она возвращалась к первому, потом опять ко второму и так далее до тех пор, пока они не встретились. Сколько пробежала собака, если ее скорость – 20 км/ч?» (638, 3 класс) Трудность в решении задачи состоит в том, что дети начинают пытаться найти расстояние, которое пробежала собака до встречи со вторым велосипедистом, потом – расстояние, которое пробежала собака до встречи с первым велосипедистом и т.д. Но это сделать практически невозможно. Важно при разборе задачи выяснить, что общего будет в движении велосипедистов и собаки. Скорости у велосипедистов и у собаки разные, разными будут и расстояния, которые проедут велосипедисты и пробежит собака, но одинаковым будет время движения. Таким образом, чтобы найти расстояние, которое пробежала собака, надо знать время, которое она бегала между велосипедистами. Оно будет таким же, какое время были в пути велосипедисты. При них мы знаем, что они ехали со скоростями 10 км/ч и вместе преодолели 20 км. Значит они были в пути 20 : (10 + 10) = 1 (ч). Столько же времени была в пути и собака, за это время она пробежала 20 · 1 = 20 (км).

Задачи, подобные следующей, также часто вызывают затруднения. Задача: «Велосипедист должен попасть в место назначения к определённому сроку. Известно, что если он поедет со скоростью 15 км/ч, то приедет на 1 ч раньше, а если скорость будет 10 км/ч, то опоздает на 1 ч. С какой скоростью должен ехать велосипедист, чтобы приехать вовремя?» (325, 4 класс) По условию задачи не очень понятно, как использовать тот факт, что велосипедист «приедет на 1 ч раньше» или «опоздает на 1 ч». Представим, что едет не один велосипедист, а одновременно выезжают два велосипедиста, причем первый доезжает до места назначения и едет дальше еще целый час. Изобразим движение велосипедистов:

Получаем, что первый велосипедист проехал после места назначения 15 км, а второй – не доехал до места назначения 10 км. Всего первый велосипедист проехал на 15 + 10 = 25 (км) больше первого, потому что ехал со скоростью на 15 – 10 = 5 (км/ч) больше. Первый велосипедист может обогнать второго на 25 км за 25 : 5 = 5 (ч). Следовательно, до места назначения он может доехать за 4 часа, при этом он проедет 15 · 4 = 60 (км). Найдем, с какой скоростью должен ехать велосипедист, чтобы прибыть на место назначения вовремя: 60 : 5 = 12 (км/ч).

Решение задач алгебраическим методом

Решение задач алгебраическим методом не подчиняется какой-либо единой, достаточно универсальной схеме. Поэтому всякое указание, относящееся ко всем задачам, носит самый общий характер.

Деятельность по решению задачи алгебраическим методом состоит из 4 этапов.

Первый этап – анализ задачи. Основное назначение этапа – осмыслить ситуацию, отраженную в задаче; выделить условия и требования, назвать данные и искомые, выделить величины и зависимости между ними (явные и неявные). На этом этапе решения задачи можно использовать такие приемы: как представление той жизненной ситуации, которая описана в задаче; постановка специальных вопросов и поиск ответов на них; «переформулировка» задачи; моделирование ситуации, описанной в задаче, с помощью реальных предметов, предметных или графических моделей и др.

Работа на первом этапе не зависит от выбранного метода решения и не имеет принципиальных отличий.

Второй этап – поиск пути решения задачи и составление плана ее решения. Его назначение – завершить установление связей между данными и искомыми величинами и указать последовательность использования этих связей.

Одним из приемов поиска пути решения задачи является анализ задачи по тексту или по ее вспомогательной модели. Поиск пути решения задачи можно осуществлять от вопроса задачи к данным (аналитический путь) или от данных к вопросу (синтетический путь).

На втором этапе (при поиске пути решения задачи и составлении плана ее решения) в случае применения алгебраического метода решения осуществляются: выбор основного соотношения для составления уравнения; выбор неизвестного и введение обозначения для него; выражение величин, входящих в основное соотношение, через неизвестное и данные.

Третий этап – осуществление плана решения задачи. Его назначение – найти ответ на требование задачи.

При алгебраическом методе осуществление плана решения задачи выполняется письменно. В этом случае описывают выбор неизвестного (неизвестных) и его обозначения; записывают, как выражаются другие величины через неизвестные и заданные числа, а также определяют соотношения, лежащие в основе математические модели задачи. Затем составляется уравнение (система уравнений и неравенств), выполняется его решение, в результате чего находится ответ на требование задачи.

Четвертый этап – проверка решения задачи. Назначение этапа – установить правильно ли понята задача, и выяснить, не противоречит ли полученный ответ всем другим условиям задачи. Этот этап является обязательным при решении задач. Следует помнить, что логичные рассуждения на других этапах решения задачи не гарантируют правильности ее решения. Проверку решения задачи можно проводить различными способами:

• установление соответствия между числами, полученными в результате решения задачи и данными в условии задачи;

• составление и решение задачи, обратной данной;

• решение задачи различными способами;

• решение задачи различными методами;

• прикидка (грубая проверка).

Рассмотрим этапы решения задачи алгебраическим методом более подробно на конкретном примере: «Из двух городов, расстояние между которыми 484 км, вышли одновременно навстречу друг другу два поезда. Скорость одного поезда 45 км/ч. Определи скорость другого поезда, если поезда встретились через 4 ч?» (333, 4 класс)

1. Анализ содержания задачи.

– О чем говорится в задаче? (В задаче идет речь о двух поездах, которые двигаются навстречу друг другу).

– Что известно в задаче? (Известно, что расстояние между городами 484 км, они встретились через 4 ч, также известна скорость одного из поездов; она равна 45 км/ч).

– Что требуется найти? (Требуется найти скорость второго поезда).

Краткую запись задачи можно представить в виде схематического чертежа.

484 км

45 км/ч

4ч

?

2.Поиск пути решения задачи и составление плана ее решения.

Обозначим скорость второго поезда через х. Зная скорость первого поезда, можем узнать скорость сближения поездов, она равна 45 +х. Тогда сможем узнать расстояние, которое прошли поезда, а значение этого расстояния мы знаем из условия задачи.

3.Осуществление плана решения задачи.

Пусть хкм/ч – скорость второго поезда. Скорость сближения поездов будет (45 +х) км/ч, а пройденное ими расстояние (45 +х)4 км. По условию расстояние равно 484 км. Составляем уравнение:

(45 + х)4 = 484.

Решив уравнение, получаем х=76.

Итак, искомая скорость равна 76 км/ч.

4. Проверка решения задачи.

Через 4 ч первый поезд пройдет 45 · 4 = 180 (км).

Через 4 ч второй поезд пройдет 76 · 4 = 304 (км).

Найдем, чему равно расстояние между поездами после четырех часов движения: 180 + 304 = 484 (км). Расхождения с условием задачи нет. Задача решена правильно.

Ответ: скорость второго поезда равна 76 км/ч.

В реальном процессе решения задачи названные этапы не имеют четких границ, и человек, решающий задачу, не всегда выделяет их в явном виде, переходя от одного к другому незаметно для себя. Вместе с тем решение каждой отдельно взятой задачи обязательно должно содержать все указанные этапы, осмысленное прохождение которых (вместе со знанием приемов их выполнения) делает процесс решения любой задачи осознанным и целенаправленным, а значит, более успешным. Игнорирование одних этапов (например, поиска пути решения) может привести к решению методом «проб и ошибок», игнорирование других (например, проверки решения задачи) – к получению неверного ответа.

Виды задач, решаемых алгебраическим методом

Уравнения являются мощным средством решения задач. Использовать уравнения можно уже при решении простых текстовых задач.

«По озеру плавало 7 уток. Когда несколько уток улетело, то на озере осталось 5 уток. Сколько уток улетело?» (143, 1 класс)

Решение. Пусть х уток улетело, тогда получим уравнение:

7 – х= 5

х= 7 – 5

х= 2

Ответ: улетели 2 утки.

Алгебраический метод можно успешно использовать и при решении составных задач.

Рассмотрим задачу: У кошки Мурки родилось 6 серых котят и 4 пёстрых. Когда несколько котят отдали в добрые руки, осталось ещё 5 котят. Сколько котят отдали в добрые руки? 365.

Решение: обозначим через хколичество отданных котят, тогда получим уравнение:

(6 + 4) – х= 5

10 – х= 5

х= 10 – 5

х= 5

Ответ: отдали 5 котят.

Рассмотрим некоторые типы задач, которые в начальной школе решаются арифметическим методом, но при их решении можно использовать также и алгебраический метод. Заметим, что если при решении задачи арифметическим методом необходимо знать некоторые особые приемы, то при решении задач алгебраическим методом необходимость в этом отпадает.

Задачи на нахождение неизвестных по их сумме и разности.

К задачам этого вида относятся задачи, в которых по известным сумме и разности двух значений некоторой величины требуется найти эти значения.

Задача: «Тетрадь вместе с обложкой стоит 12 руб., причём бумага на 10 руб. дороже обложки. Сколько стоит бумага и сколько стоит обложка в отдельности?» (705, 4 класс)

Решение. Удобнее через хобозначать меньшее число. Пустьхруб. стоит обложка, тогда бумага стоит (х+10) руб., а вся тетрадь стоит (х+ 10) +хруб. Зная, что тетрадь с обложкой стоит 12 руб., составляем уравнение:

(х+ 10) +х= 12

2х+ 10 = 12

2х= 12 – 10

2х= 2

х= 2 : 2

х= 1

Получаем, что бумага стоит 1 руб., а обложка 1 + 10 = 11 руб.

Задача на нахождение неизвестных по их сумме или разности и кратному отношению.

К задачам этого вида относятся задачи, в которых по известным сумме или разности и частному двух значений некоторой величины требуется найти эти значения. Задача. «Кошка легче собаки в 4 раза, а вместе они весят 30 кг. Сколько весит кошка и сколько собака?» (678, 4 класс) Если при решении такого типа задачи арифметическим методом требовалось выполнить чертеж, то, решая задачу алгебраическим методом, выполнение чертежа становится необязательным.

Решение. Если при решении предыдущей задачи обозначение меньшего числа через хбыло желательным, но не обязательным условием, то при решении задач, в которых указано кратное отношение, обязательно обозначаем черезхто число, которое меньше. Пустьхкг весит кошка, тогда собака весит 4хкг. Вместе собака и кошка весят (х+ 4х) кг. По условию задачи они вместе весят 30 кг. Составляем уравнение:

х+ 4х= 30

5х= 30

х= 30 : 5

х= 6

6 4 = 24 (кг)

Ответ: кошка весит 6 кг, а собака весит 24 кг.

Ответ: 144 пассажира находится в купейных вагонах, 576 пассажиров – в плацкартных вагонах.

Задачи на «предположение» также можно решить при помощи уравнения, однако, при составлении уравнения надо с особой тщательностью подойти к тому, что принять за х, т.к. в одном случае уравнение будет хорошо решаться, а в другом – будет необходимо вычитать из меньшего числа большее, чего дети в начальной школе не делают. Рассмотрим задачу: «На поле пасутся кони. Их пасут ребята. Если пересчитать ноги лошадей и детей, то будет 74, а если пересчитать головы, то 22. Сколько на поле лошадей и сколько пастухов?» (714, 4 класс)

За хможно принять число детей или число лошадей. Рассмотрим первый вариант: пустьх– число детей, тогда лошадей будет 22 –х. Ног у всех детей будет 2х, а у всех лошадей – 4(22 –х). Тогда всего ног будет 2х+ 4(22 –х). По условию задачи ног всего 74. Составляем уравнение: 2х+ 4(22 –х) = 74. Раскрыв скобки, получаем: 2х+ 88 – 4х= 74. Нам придется из 2хвычитать 4х, что на данном этапе изучения младшими школьниками математики невозможно. Поэтому примем захчисло лошадей, тогда получим уравнение: 4х+ 2(22 –х) = 74. Решив уравнение, получим, что на поле было 15 лошадей и 7 пастухов.

Применять алгебраический метод, как было показано выше, можно и к задачам на движение. Рассмотрим еще один пример применения данного метода на следующей задаче: «Два автомобиля выехали одновременно из одного пункта в одном направлении со скоростями 40 км/ч и 55 км/ч. Через сколько часов расстояние между ними будет 90 км?» (324, 4 класс)

В данной задаче за худобно принять время, в течение которого двигались лыжники. Тогда можно узнать расстояние, которое прошел каждый лыжник за это время. Первый лыжник прошел 40хкм, а второй – 50хкм. Т.к. они выехали одновременно из одного пункта в одном направлении, то 90 км – это разность между расстояниями, которые прошли лыжники. Составляем уравнение: 50х– 40х= 90. Получаем, что расстояние между лыжниками будет 90 км через 9 часов. Для данной задачи решение алгебраическим методом получается проще, чем арифметическим, т.к. приходится находить разность расстояний, которые прошли лыжники, а не скорость удаления.

Данный метод также хорошо применим для решения задач, связанных с нахождением периметра или площади фигур. Рассмотрим задачу: «Периметр прямоугольника равен 48 см, а длина его на 2 см больше ширины. Найди площадь этого прямоугольника.» (484, 4 класс) Пусть х см – ширина прямоугольника, тогда его длина равнах+ 2 см. Периметр прямоугольника равен (х+ (х + 2))2. А по условию задачи периметр прямоугольника равен 48 см. Составив и решив уравнение, получим, что ширина прямоугольника равна 11 см, а ее длина 13 см. осталось найти его площадь: 1113 = 143 см².

С помощью уравнений можно решать нестандартные задачи. Рассмотрим задачу: «Дочери 8 лет, а матери 38. Через сколько лет мать будет втрое старше дочери? (695, 4 класс).

Нужно узнать, через сколько лет мать будет в 3 раза старше дочери. Обозначим это неизвестное через х. Дочери сейчас 8 лет, значит черезхлет ей станет 8 +хлет, а матери 38 +хлет. Зная, что дочь в 3 раза моложе, составляем уравнение:

(8 + х) · 3 = 38 +х

24 + 3х–х= 38 –х

24 + 2х= 38

24 – 24 + 2х= 38 – 24

2х= 14

х= 14 : 2

х= 7

Ответ: через 7 лет мать будет в 3 раза старше дочери.

Часто алгебраический метод оказывается для решения той или иной задачи проще, для него нет необходимости знать особые приемы решения, зачастую алгебраический метод можно использовать для того, чтобы догадаться, как решить задачу арифметическим методом. Данный метод выступает в начальной школе как пропедевтика к изучению курса алгебры, поэтому должен занимать достойное место в начальном курсе математики.

Задачи, требующие особых приемов решения

Задачи на нахождение чисел по сумме и разности.

В задачах такого вида известна сумма двух чисел и их разность, причем часто разность бывает выражена словами «больше на». Обучение решению таких задач можно начать совсем с простого примера: «Белка 8 орехов разложила в два дупла, причем в первом оказалось на 2 ореха больше, чем во втором. Сколько орехов положила белочка в каждое дупло?» Т.к. в данной задаче числа совсем маленькие, то дети могут найти ответ даже подбором. Затем учитель задет вопрос: «Сколько орехов надо убрать из первого дупла, чтобы орехов в дуплах стало поровну?». Т.к. в первом дупле на 2 ореха больше, то надо убрать 2 ореха. Тогда выясняем, сколько орехов осталось в дуплах, после того, как эти 2 «лишних» ореха убрали; их будет 6, причем в первом и во втором дупле их будет одинаковое количество. Остается 6 разделить на 2, тем самым узнать, сколько орехов было во втором дупле. А чтобы узнать, сколько орехов было в первом дупле, надо к трем прибавить 2. Получаем, что в одном дупле было 5 орехов, а во втором – 3. Для решения задач такого типа необходимо выполнить чертеж, тогда решение задачи становится практически очевидным. При решении задач такого типа существует трудность в записи пояснения после первого действия. Например, при решении данной задачи после действия 8 – 2 = 6 мы должны записать: «столько орехов было бы в двух дуплах, если бы во втором дупле было столько орехов, сколько в первом». Как видим, запись получается очень дленная, поэтому при решении таких задач можно разрешить ученикам записывать два действия в одно: (8 – 2 ) : 2 = 3 (ор.) – было в первом дупле.

Рассмотрим еще одну задачу такого типа: «Три брата поймали 29 карасей. Когда один брат отложил для ухи 6 штук, другой – 2, а третий – 3, то у каждого осталось равное количество рыб. Сколько карасей поймал каждый из них?», (635, 3 класс) Построим графическую модель:

Первый брат

Второй брат

Третий брат

По чертежу видно, что для того чтобы уравнять число карасей, пойманных каждым братом, надо вычесть из общего количества пойманных рыб отложенные для ухи рыбы.

1. 6 + 2 + 3 = 11 (к.) – отложили братья для ухи;

2. 29 – 11 = 18 (к.) – у них осталось;

3. 18 : 3 = 6 (к.) – осталось у каждого;

4. 6 + 6 = 12 (к.) – поймал первый брат;

5. 6 + 2 = 8 (к.) – поймал второй брат;

6. 6 + 3 = 9 (к.) – поймал третий брат.

Задачи на нахождение чисел по сумме или разности и кратному отношению.

В задачах такого вида известно, во сколько раз одно число больше или меньше другого, а также известна сумма или разность этих чисел. Начнем рассмотрение данного вида задач со следующего примера: «На двух полках стояло 18 книг, причем на второй полке книг было в 2 раза больше чем на первой. Сколько книг стояло на каждой полке?» Так же, как в предыдущем случае, выполним чертеж (он также является необходимым условием успешного овладения умения решать задачи такого вида).

I

18

II

По чертежу видно, что все книги составляют 3 части, тем не менее, это действие можно записать: 1 + 2 = 3 (части) – составляют 18 книг. Вторым действием находим число книг на первой полке и третьим – число книг на второй полке.

Рассмотрим еще ряд задач, условия о сумме или разности даны в условии задачи не в столь явном виде: «В двух коробках 18 кубиков. Число кубиков в одной коробке составляет половину кубиков другой коробки. Сколько кубиков в каждой коробке?» (653, 3 класс) В задаче сказано, что число кубиков в одной коробке составляет половину кубиков другой коробки. При построении графической модели необходимо определиться, кубики в какой коробке принять за одну часть. Обычно за одну часть принимаем то, что меньше. Так и в данной задаче: в первой коробке кубики составляют половину числа кубиков во второй коробке, по-другому это можно сказать так: «во второй коробке кубиков в два раза больше», поэтому за одну часть примем кубики первой коробки, тогда в другой коробке кубики составят 2 части.

Еще одна задача: «Банка с мёдом весит 500 г. Та же банка с керосином весит 350 г. Керосин легче мёда в 2 раза. Сколько весит пустая банка?» (692, 4 класс) В данной задаче разность масс банки с медом и банки с керосином неизвестна, но ее легко найти, при этом следует обратить снимание детей на то, что 500 г – это масса пустой банки и масса мёда, а 350 г – это масса пустой банки и масса керосина. Когда мы из 500 г вычтем 350 г, то получим разницу масс мёда и керосина, т.к. банки по массе были одинаковые. Сделаем чертеж:

500 г

мёд

банка

350 г

банка

керосин

Примем за одну часть массу керосина, тогда масса мёда будет составлять две такие части. Первым действием из 500 г вычтем 350 г, найдем, что 150 г – масса керосина, а масса мёда 150 2 = 300 г.

Рассмотрим еще две задачи данного типа, которые носят олимпиадный характер: «Дочери в настоящее время 8 лет, а матери 38. Через сколько лет мать будет втрое старше дочери?» (695, 4 класс). Для того чтобы решить эту задачу, главное, что должен понять ученик, это то, что разница между возрастом матери и дочери в любой момент времени будет одинаковой. Поэтому эту задачу можно переформулировать таким образом: «Мать втрое старше дочери. Сколько лет дочери, если она младше матери на 30 лет?» Данная задача уже не должна вызвать затруднений. Получаем, что разница между возрастом матери и возрастом дочери составляет 2 части или 30 лет, т.е. дочери 30 : 2 = 15 лет. Вернемся к первоначальной задаче. В ней требовалось узнать, через сколько лет мать будет втрое старше дочери. Известно, что в настоящее время дочери 8 лет, а в момент, когда мать будет втрое ее старше, ей будет 15 лет. Отвечаем на вопрос задачи: 15 – 8 = 7 (лет) – через столько лет мать будет втрое старше дочери.

Другая задача: «На первой грядке росло в 5 раз больше кустов клубники, чем на второй. Когда с первой грядки пересадили 22 куста на вторую грядку, то число кустов клубники на каждой грядке стало одинаковым. Сколько было кустов на каждой грядке?» (723, 4 класс)

С

22

ложность при решении задачи состоит в том, чтобы правильно определить разность между количеством кустов клубники на первой и на второй грядках. Для этого выполним чертеж:

I

22

II

По чертежу видно, что на первой грядке было на 22 + 22 = 44 куста или на 4 части больше, чем на второй. Получаем, что на второй грядке было 44 : 4 = 11 кустов, а, следовательно, на первой грядке кустов было 11 5 = 55 кустов. Сделаем проверку: 55 – 22 = 33, 11 + 22 = 33. Задача решена правильно.

Еще одна, немного более сложная задача: «Ученик сказал, что за 4 дня он решил 23 задачи. Причем каждый новый день он решал больше задач, чем в предыдущий, а в четвертый день он решил в 2 раза больше задач, чем в первый. Сколько задач решал ученик каждый день? (631, класс) Так же, как и в предыдущем случае, построим графическую модель:

I

II

III

IV

Сложность при решении данной задачи состоит в том, что здесь не указано, на сколько больше задач решал ученик во второй и в третий день по сравнению с первым. Тем не менее, начнем решать с задачу с выяснения, что было бы, если бы во второй и в третий дни ученик решал по столько же задач, сколько в первый (можно на чертеже закрыть отрезки, показывающие «лишние» задачи, решенные во второй и в третий дни). Получается, что оставшиеся задачи составляют 5 частей. Находим ближайшее число, меньшее 23, которое делится на 5. Это число 20. Найдем число задач, которые решил ученик в первый день: 20 : 5 = 4 (задачи). Найдем, сколько еще задач решил ученик во второй и третий дни: 23 – 20 = 3 (задачи). Поскольку в третий день он решил больше задач, чем во второй, то получаем, что во второй день он решил на одну задачу больше по сравнению с первым днем, а в третий – на две задачи больше. Таким образом, в первый день ученик решил 4 задачи, во второй – 5 задач, в третий – 6 задач, а в четвертый 8 задач.

Если бы мы взяли не наибольшее число, делящееся на 5, а число 15, то получили бы, что в первый день ученик решил 3 задачи, в четвертый 6 задач, а во второй и третий дни на 8 задач больше по сравнению с тем, что если бы он решал в эти дни по столько же задач, сколько решил в первый день. Но число 8 мы не сможем представить в виде суммы двух слагаемых, каждое из которых меньше 3. Таким образом, задача имеет единственное решение.

Задачи на предположение.

Рассмотрим задачу: «Во дворе ходят индюки и козочки, у всех вместе 44 ноги и 14 голов. Сколько индюков и козочек ходят во дворе?» (628, 3 класс) В большинстве задач такого типа указаны не все числовые данные. Так, в данной задаче для решения необходимы данные о числе ног у индюка и у козочки.

Краткую запись для данной задачи можно сделать следующую:

И

14 голов

44 ноги

ндюки 2 ноги

Козочки 4 ноги

В данной задаче мы должны предположить, что у индюков и у коз одинаковой количество ног. Представить это не так просто, поэтому нужно придумать какую-нибудь ситуацию, например, все козы стоят только на двух задних ногах. Тогда, посчитав все ноги и найдя разницу между посчитанными ногами и количеством ног на самом деле, т.е. в нашей ситуации это передние ноги коз, можно найти число коз, зная, что у каждой козы по 2 передние ноги. Решение задачи будет таким:

1) Сколько ног было бы у коз и индюков, если бы у всех было по 2 ноги?

2 14 = 28 (ног)

2) На сколько ног на самом деле больше?

44 – 28 = 16 (ног)

3) Сколько во дворе козочек?

16 : 2 = 8 (коз)

4) Сколько ног у козочек?

4 8 = 32 (ноги)

5) Сколько ног и индюков?

44 – 32 = 12 (ног)

6) Сколько индюков?

12 : 2 = 6 (индюков)

Сделаем проверку: 4 8 + 26 = 44 (ноги), следовательно, задача решена правильно.

Можно было сделать и другое предположение, что у коз и у индюков по 4 ноги, но эту ситуацию представить сложнее.

Рассмотрим еще одну задачу: «Стрелок 10 раз выстрелил по мишени и выбил 90 очков. Сколько было попаданий в семёрку, восьмёрку и девятку, если десяток было четыре, а других попаданий и промахов не было?» (684, 4 класс) Данная задача гораздо сложнее предыдущей, кроме того, она имеет не единственное решение.

Вначале узнаем, сколько очков было выбито при попадании в десятку: 10 4 = 40 (очков). Тогда можно найти число очков при попадании в семёрку, восьмёрку и девятку: 90 – 40 = 50 (очков). Т.к. всего выстрелов было 10, а попаданий в десятку было 4, то можно также узнать число остальных попаданий: 10 – 4 = 6. Получается, что, выстрелив 6 раз, выбили 50 очков. Предположим, что все 6 раз попали в семерку, тогда было бы выбито 76 = 42 (очка), а на самом деле было выбито на 50 – 42 = 8 (очков) больше. Если бы вариантов попадания было только два, то задача решалась бы точно так же, как предыдущая, но в нашей задаче попадания были семёрку, восьмёрку и девятку. Поэтому нам необходимо представить число 8 в виде суммы не шести слагаемых, каждое из которых равно 0, 1 или 2. Возможны три варианта: 0 + 0+ 2 + 2 + 2 + 2, 0 + 1 + 1 + 2 + 2 + 2 или 1 + 1 + 1 + 1 + 2 + 2. Таким образом, задача имеет три решения: 1) стрелок попал 2 раза в семерку, 4 раза в девятку и 4 раза в десятку; 2) стрелок попал один раз в семерку, два раза в восьмерку, 3 раза в девятку и 4 раза в десятку; 3) стрелок попал 4 раза в восьмерку, 2 раза в девятку и 4 раза в десятку. Если понимать условие задачи так, что попадания в семерку, восьмерку и девятку должны быть обязательно, то остается одно второе решение.

Еще одна задача: «Несколько детей собирали макулатуру. Каждый мальчик собрал по 21 кг, а каждая девочка – по 15 кг. Всего ребята собрали 174 кг макулатуры. Сколько мальчиков и сколько девочек собирали макулатуру?» (702, 4 класс) Сложность задачи состоит в том, что не указано общее число мальчиков и девочек, принимавших участие в сборе макулатуры. Предположим, что в сборе макулатуры принимали участие одни девочки, т.е. каждый собрал по 15 кг макулатуры. Узнаем, сколько раз по 15 содержится в 174 кг, т.е. сколько человек принимало участие в сборе макулатуры: 174 : 15 = 11 (ост. 9). Т.е. можно предположить, что в мы имеем 11 пачек с макулатурой по 15 кг и еще 9 кг. Узнаем, на сколько килограммов макулатуры собрал каждый мальчик: 21 – 15 = 6 (кг). Но разделить 9 кг по 6 кг мы не можем, значит, наше предположение о том, что в сборе макулатуры принимало участие 11 человек неверно. «Развяжем» одну пачку с макулатурой, получим 10 пачек по 15 кг и еще 24 кг (15 кг + 9 кг). Нам надо в некоторые пачки добавить по 6 кг. Разделив 24 кг на 6 кг, получим, что пачек по 21 кг будет 4, т.е. в сборе макулатуры приняло участие 4 мальчика, девочек: 10 – 4 = 6. сделаем проверку: 21 4 + 156 = 84 + 90 = 174 (кг), задача решена верно.

Нестандартные задачи

Логические задачи на установление взаимно однозначного

отношения между множествами

Рассмотрим задачу, в которой устанавливается взаимно однозначного соответствия между множествами, причем все высказывания истинные: «Валя, Галя и Даша одеты в платья трёх цветов – красное, голубое и жёлтое. Валя не в красном и не в голубом, а Галя не в красном платье. Какого цвета платье на каждой из девочек?» (657, 3 класс)

Для решения задачи можно использовать таблицу, в которой в столбик запишем содержимое сундуков, а в строчку – цвет сундука. Данные задачи внесем в соответствующие клетки таблицы, например, знаками «+» (положительный результат) или «–» (отрицательный результат). Т.к. между множествами устанавливается взаимно однозначное соответствие, то, заполняя таблицу, мы в каждом столбце (строке) можем поставить только один знак «+». В остальных клетках этого столбца (строки) будут стоять знаки «–». При решении задачи такого вида не стоит сразу делать те или иные выводы по условию задачи, лучше вначале полностью условие задачи внести в таблицу. Если ни одно условие не будет пропущено, то знаки «+» в таблице расставляются практически автоматически.

Начертим таблицу 4 ´4

	Красное	Голубое	Желтое
Валя	-	-	+
Галя	-	+	-
Даша	+	-	-

В левом столбце напишем имена девочек, в верхней строке – цвета платьев. По условию Валя не в красном и не в голубом, а Галя не в красном платье, поставим в таблице в соответствующих клетках «–». Т.к. Валя не в красном и не в голубом платье, остается, что она в желтом; поставим в соответствующей клетке таблицы «+». Как только мы получили «+», в остальных клетках этого столбца ставим «–».Тогда получаем, что Галя не в красном платье и не в желтом, значит, она – в голубом. Остается, что Даша была в красном платье.

Эту задачу нетрудно решить без таблицы – перебором. Но если нужно установить соответствие между двумя множествами, каждое из которых содержит по пять или более элементов, то без использования таблиц это сделать достаточно сложно. Применение таблиц значительно ускоряет, почти автоматизирует решение задачи.

Рассмотрим еще одну задачу: «Гном разложил свои сокровища в 3 сундука разного цвета: в один – драгоценные камни, в другой – золотые монеты, в третий – магические книги. Он помнит, что красный сундук находится правее, чем сундук с камнями, и что сундук с книгами – правее красного сундука. В каком сундуке лежат книги, если зеленый сундук стоит левее синего и зеленый и синий сундуки – крайние.» (633, 3 класс) На первый взгляд она очень похожа на предыдущую, однако решать ее при помощи таблицы не совсем удобно, т.к. сложно по условию задачи понять, что в каком сундуке не лежит. Решим эту задачу по-другому. В задаче сказано, что красный сундук находится правее, чем сундук с камнями, и что сундук с книгами – правее красного сундука, т.е. сундуки располагаются в таком порядке: сундук с камнями, красный сундук, сундук с книгами. По условию задачи также сказано, что зеленый и синий сундуки – крайние, и зеленый сундук стоит левее синего; подпишем цвет сундука под левым и правым сундуками. Получим такую запись:

с камнями красный с книгами

зеленый синий

Из этой записи следует, что в зеленом сундуке лежат драгоценные камни, книги лежат в синем сундуке, остается, что в красном сундуке – магические книги.

Решим еще одну задачу: «В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3?» (683, 4 класс) Сложность в решении задачи состоит в том, что в формулировке задачи нет ни одного очевидного условия. Начертим таблицу:

	5	8	13	15
Аня	-	-	+	-
Боря	-	+	-	-
Вера	+	-	-	-
Галя	-	-	-

Т.к. в детский сад по условию задачи ходит девочка, то Боре не может быть 5 лет, ставим в соответствующей клетке «–». Также в условии задачи сказано, что Аня старше Бори, значит Ане не может быть 5 или 8 лет. Остается, что Ане может быть 13 или 15 лет, но число 15 в сумме ни с одним из оставшихся чисел не делится на 3, что противоречит условию, что сумма лет Ани и Веры делится на 3. Получается, что Ане 13 лет, тогда Боре – 8 лет. Расставим в остальных клетках первой и второй строки, а также во втором и третьем столбце знаки «–». Т.к. сумма лет Ани и Веры делится на 3, а Ане 13 лет, то получаем, что Вере 5 лет, тогда Гале 15 лет.

В следующей задаче из трех высказываний истинно только одно, при этом неизвестно какое. Для того чтобы решить задачу, рассмотрим три варианта: истинно первое высказывание, истинно второе высказывание и истинно третье высказывание. Задача: «Три класса участвовали в туристической эстафете. Один класс занял 1 место, другой – 2 место, а третий – 3 место. Перед началом соревнований болельщики заявили: 4 «А» займет 1 место; 4 «В» не займет 1 место; 4 «Б» не будет последним. Одно из этих предположений оказалось верным, а два других – ошибочными. Какое место занял каждый из четвертых классов?» (632, 3 класс)

Пусть истинным будет высказывание первого болельщика, а высказывания второго и третьего болельщиков были ложными. Это означает, что 4 «А» занял первое место и 4 «В» также занял первое место. Получили противоречие. Допустим, что прав был второй болельщик, а два других ошиблись. Это означает, что 4 «А» не занял 1 место; 4 «В» не занял 1 место; 4 «Б» был последним. Этот вариант тоже не годится. Предположим, что прав был третий болельщик. Тогда 4 «А» не занял 1 место; 4 «В» занял 1 место; 4 «Б» не был последним, т.е. на первом месте был 4 «В» класс, на втором - 4 «Б» класс, а на третьем 4 «В» класс. Все рассуждения, приведенные выше, можно оформить в виде таблицы.

	По условию задачи	Случай 1	Случай 2	Случай 3
Первый зритель	4 «А» – 1	И 4 «А» – 1	Л 4 «А» – не 1	Л 4 «А» – не 1
Второй зритель	4 «В» – не 1	Л 4 «В» – 1	И 4 «В» – не 1	Л 4 «В» – 1
Третий зритель	4 «Б» – не 3	Л 4 «Б» – 3	Л 4 «Б» – 3	И 4 «Б» – не 3
		Противоречие	Противоречие	4 «В», 4 «Б», 4 «А»

Рассмотрим еще один способ решения задачи. Составим все возможные варианты распределения мест и посмотрим, в каком из этих случаев прав будет только один зритель.

Поставим «+», если зритель угадал исход соревнований, и «-», если зритель ошибся.

Распределение мест	Первый зритель	Второй зритель	Третий зритель
4 «А», 4 «Б», 4 «В»	+	+	+
4 «А», 4 «В», 4 «Б»	+	+	-
4 «Б», 4 «А», 4 «В»	-	+	+
4 «Б», 4 «В», 4 «А»	-	+	+
4 «В», 4 «А», 4 «Б»	-	-	-
4 «В», 4 «Б», 4 «А»	-	-	+

Из таблицы видно, что только в последней строке таблицы соблюдается условие задачи, что прав был один зритель.

Возможен еще один вариант решения задачи: высказывания первого и второго болельщика не могут принимать разные значения истинности, т.к. в этом случае или оба класса займут одновременно первые места, или одновременно не могут быть и на первом месте и на третьем. Получается, что высказывания первых двух болельщиков могут быть только одновременно ложными. Дальше решение задачи становится понятным.

Рассмотрим еще задачу, в которой все высказывания составные, часть каждого высказывания истинна, а другая – ложная. При решении задач данного вида поступают так: берут одну часть высказывания одного из лиц и предполагают, что она истинна. Если при этом, рассматривая утверждения других членов группы, мы не придем к противоречию, то делается вывод, что взятое нами исходное утверждение истинно. Если же пришли к противоречию, то делается вывод, что взятое нами за истинное утверждение является ложным, и, следовательно, вторая часть этого утверждения является истинной. Пусть необходимо решить задачу: «Три ученика различных школ Великого Новгорода приехали на отдых в один летний лагерь. На вопрос вожатого, в каких школах Великого Новгорода они учатся, каждый дал ответ.

Петя: «Я учусь в школе № 24, а Лёня – в школе № 8».

Лёня: «Я учусь в школе № 24, а Петя – в школе № 30».

Коля: «Я учусь в школе № 24, а Петя – в школе № 8».

Вожатый, удивлённый противоречиями в ответах ребят, попросил их объяснить, где правда, а где ложь. Тогда ребята признались, что в ответе каждого из них одно утверждение верно, а другое – ложно. В какой школе учится каждый из мальчиков?» (685, 4 класс)

Предположим, что верно первое утверждение Пети, тогда ложны второе утверждение Пети и первые утверждения Лени и Коли. Но при этом истинными должны быть вторые утверждения Лени и Коли. Получили, что Петя учится сразу в трех школах, значит наше предположение о том, что первое утверждение Пети истинно, неверно.

Предположим, что его второе утверждение верно. Тогда ложными будут первые утверждения Лени и Пети и второе утверждение Коли. При этом истинным оказалось второе утверждение Лени и первое утверждение Коли. Здесь противоречия нет. Получаем, что Леня учится в школе № 8, Петя – в школе № 30, Коля – в школе № 24.

Решение задачи т удобно оформлять так:

П – 24 иЛ – 8л

Л – 24 лП – 30и

К – 24 лП – 8и противоречие

П – 24 лЛ – 8и

Л – 24 лП – 30и

К – 24 иП – 8л Лёня – в школе № 8, Петя – в школе № 30, Коля – в школе № 24.

Задачи, решаемые при помощи графов

Некоторые логические задачи целесообразно решать с помощью графов. Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

Точки, изображающие элементы множества, называются вершинами графа; отрезки – ребрами графа. При помощи графа легко можно изобразить отношения между элементами множества. Рассмотрим задачу: «Трое друзей играли в шахматы. Каждый сыграл 2 партии. Сколько всего партий было сыграно?» (659, 3 класс). Изобразим мальчиков точками, а их рукопожатия – отрезками, тогда ответом на вопрос будет число ребер данного графа.

По графу сразу становится понятно, что всего было сыграно 3 партии. С помощью графа можно найти общий способ решения задачи: от каждой точки мы провели по 2 отрезка, а точек на графе 3, умножаем 2 на 3, получаем 6. Но каждый отрезок мы посчитали 2 раза; разделив 6 на 2, получим ответ на вопрос задачи. Такой способ решения будет необходим при решении при решении задач с большим числом участников, когда построение графа будет затруднительно. Например, есть 15 городов, каждый из которых соединён с остальными автобусными маршрутами. Необходимо сосчитать число таких маршрутов. Их будет 15 · 14 : 2 = 105.

Рассмотрим обратную задачу: «Участники шахматной олимпиады сыграли друг с другом по одной партии. Всего было сыграно 6 партий. Сколько было участников?» (675, 3 класс)

Предположим, что сыграли два мальчика, изобразим их точками, а сыгранную партию линией, соединяющей эти точки (рис. 1). Добавляем третьего участника и получаем три партии (рис. 2). Значит, необходимо добавить еще четвертого участника. Если сыграли четыре мальчика, то сыгранных партий будет шесть (рис. 3). Таким образом, всего было сыграно 6 партий.

рис. 1 рис. 2 рис. 3

Задачи на принцип Дирихле

Этот принцип можно сформулировать следующим образом: «Если «вещей» больше чем «ящиков», то по крайней мере в одном «ящике» будет больше двух «вещей». Задачи такого типа бывают двух видов: на доказательство и на нахождение наименьшего числа вещей, которые надо взять не глядя, чтобы было выполнено сказанное в задаче условие. Рассмотрим задачу: «В школе 400 учеников. Верно ли, что хотя бы два ученика этой школы отмечают свой день рождения в один и тот же день года?» (547, 3 класс) В качестве «вещей» в задаче выступают учащиеся, а в качестве «ящиков» - дни года. Учащихся по условию задачи 400, а дней в году 366; учащихся больше, поэтому по крайней мере двое из них будут праздновать свой день рождения в один день. Можно рассуждать по-другому: предположим, что учащиеся празднуют дни рождения в разные дни, тогда таких учащихся может быть 366, значит еще один учащийся, не входящий в это число учеников, будет праздновать свой день рождения вместе с кем-нибудь из этих 366.

В следующей задаче необходимо найти наименьшее число предметов, которые надо взять, например: «В корзине яблоки трёх сортов. Какое наименьшее число яблок необходимо взять из корзины, не заглядывая в неё, чтобы среди них оказалось по крайней мере 2 яблока одного сорта?» (709, 4 класс) В этих задачах надо вначале рассмотреть крайний вариант, когда нам «не везет». Предположим, что мы взяли три яблока, и все они разных сортов. Если мы возьмем еще одно яблоко (четвертое), то оно окажется обязательно того же сорта, что и одно из трех взятых яблок, т.е. два яблока одного сорта у нас обязательно будет.

Решим еще оду задачу: «В мешке лежало 10 пар чёрных и 10 пар коричневых перчаток, все они перепутаны. Какое наименьшее количество перчаток необходимо взять из мешка, не заглядывая в него, чтобы скомплектовать хотя бы одну пару одноцветных перчаток?» (710, 4 класс) Предположим, что мы достали все черные перчатки на левую руку и все коричневые перчатки на левую руку, т.е. всего достали 20 перчаток. Тогда следующая, двадцать первая перчатка обязательно составит пару. Таким образом, нам для достижения результата потребуется 21 перчатка.

Следующая задача отличается от предыдущих тем, что в коробке лежит разное количество шаров одного и другого цвета и требуется достать шаров того и другого цвета также разное количество. Задача: «В коробке лежат 7 синих и 5 красных шаров. Какое наименьшее количество шаров необходимо достать (не глядя), чтобы среди них было по крайней мере 2 синих и 1 красный?» (727, 4 класс) Предположим, что мы достали все шары одного цвета. Худший вариант – все шары синие. Тогда восьмой шар будет обязательно красным. Два синих и один красный шар мы обязательно достанем.

Задачи на планирование действий

К задачам данного типа относятся задачи на расстановки, на переправы, на переливания, на дележи, на взвешивания и др. Рассмотрим известную задачу на переправу: «Как перевезти в лодке с одного берега на другой волка, козла и капусту, если известно, что волка нельзя оставить без присмотра с козлом, а козёл неравнодушен к капусте? В лодке только 2 места, поэтому с собой на борт можно брать или одно животное, или капусту.» (686, 4 класс) Если решать задачу практическим путем, то она становится не очень трудной. Сложнее оформить решение задачи письменно. Пусть все персонажи задачи находятся на левом берегу, и им требуется перебраться на берег правый. Направление переправы будем обозначать стрелкой. Введем обозначения: Ч– человек,В– волк,К– коза,к– капуста.

Вк

Вк К

В К

В к

К к

К кВ

кВ

По данной записи можно легко восстановить ход решения задачи, кроме того мы можем без труда отследить, кто из персонажей задачи находится на том или на другом берегу.

Еще один тип задач на планирование действий – задачи на расстановки. Рассмотрим задачу: «Здание имеет 4 стены. На каждой стене висят по 3 флага на одинаковом расстоянии друг от друга. Сколько флагов на здании?» (715, 4 класс) С одной стороны, можно рассуждать так: флаги висят по 3 с каждой из четырех сторон, т.е. количество флагов можно найти, умножив 3 на 4; в результате получим 12 флагов. Но это возможно, только если здание имеет форму квадрата. Флагов может быть и меньше, если повесить флаги по углам. Флаги могут быть расположены на двух противоположных углах или на всех углах здания (если оно имеет квадратную форму). Таким образом флагов может быть 12, 10 или 8.

Рассмотрим еще несколько нестандартных задач. В сборниках занимательных задач достаточно часто встречаются задачи, в которых известно расстояние между предметами и количество предметов, требуется найти расстояние между крайними предметами. К задачам такого типа также можно отнести задачи, связанные с ударом молота, с распиловкой бревен, с этажами в доме и т.д. рассмотрим задачу: «Длина бревна 6 м. За 1 мин от него отпиливают по 1 м. За сколько минут будет распилено всё бревно?» (550. 3 класс) Следует отметить, что количество метровых бревнышек будет на одно меньше, чем количество распилов. Разделив 6 на 1, получим, что метровых бревен получилось 6, их на одно меньше, чем число распилов. Таким образом, распилов будет 5 и на каждый требуется 1 минута, всего бревно будет распилено через 5 мин.

Литература

1. Бантова М.А. и др. Методика преподавания математики в начальных классах. Под ред. М.А. Бантовой. Учеб. пособие для учащихся школьных отд-ий пед. училищ. М., «просвещение», 1976.

2. Белошистая А.В. Методика обучения математике в начальной школе:: курс лекций: учеб. Пособие для студентов высш. пед. заведений. – М.: Гуманитар. Изд. Центр ВЛАДОС, 2005

3. Демидова Т.Е., Тонких А.П. Теория и практика решения текстовых задач: Учеб. пособие для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия», 2002.

4. Дрозд В.Л. и др. Методика начального обучения математике. Под ред. А.А. Столяра, В.Л. Дрозда. Минск, «Вышэйшая школа», 1988.

5. Истомина Н.Б. Методика обучения математики в начальных классах: Учеб.пособие для студ.сред. и высш.пед.учеб.заведений – М.: Издательский центр «Академия», 2002.

6. Максимова Т.Н.Сборник текстовых задач по математике: 3 класс. – М.: ВАКО, 2010.

7. Максимова Т.Н.Сборник текстовых задач по математике: 4 класс. – М.: ВАКО, 2010.

8. Мокрушина О.А.Сборник текстовых задач по математике: 1 класс. – М.: ВАКО, 2010.

9. Мокрушина О.А.Сборник текстовых задач по математике: 2 класс. – М.: ВАКО, 2010.

10. Моро М.И., Пышкало А.М. Методика обучения математике вI–IIIклассах. Пособие для учителя. М., «просвещение», 1978.

11. Свечников А.А.Решение математических задач в 1 – 3 классах. Пособие для учителя. М., «Просвещение», 1976.

57