
Методичка_Excel_2014 (2)
.pdf3.1.3 Подсчет количества пустых ячеек в диапазоне
СЧИТАТЬПУСТОТЫ(Диапазон) - категория статистических функций.
Пример 3.4. В ячейки С1, С2, С3, С4, С5 скопируйте информацию из соответствующих ячеек столбца А, оставив пустой ячейку С3: С1=1500, С2=2500, С3=«», С4=3000, С5=3500. Требуется подсчитать количество пустых ячеек в диапазоне С1:С5.
Решение.
Результат должен быть получен в ячейке С6. Пошаговыми действиями в ячейку С6 следует ввести формулу: =СЧИТАТЬПУСТОТЫ(С1:С5). В ячейке С6 получится число 1.
3.1.4 Подсчет количества непустых ячеек в диапазоне, удовлетворяющих заданному условию
СЧЕТЕСЛИ(Диапазон;Критерий) - категория статистических функций.
•Диапазон - это диапазон, в котором определяется критерий;
•Критерий - указывается в виде числа, выражения или текста и определяет, какие ячейки надо подсчитывать.
Пример 3.5. Подсчитать количество непустых ячеек в диапазоне С1:С5, значение которых больше или равно 3000.
Решение.
Результат должен быть получен в ячейке С7. Пошаговыми действиями в ячейку С7 следует ввести формулу: =СЧЕТЕСЛИ(С1:С5;«>=3000»). В ячейке С7 получится число 2.
Увеличьте значение ячейки С2 на 4000. Проследите изменение результата вычислений.
В Excel также существует встроенная функция для подсчета количества ячеек, значения в которых удовлетворяют нескольким критериям -
СЧЕТЕСЛИМН(Диапазон_условия1;Условие1;Диапазон_условия2;Условие2;….).
Пример 3.6. В диапазоне С1:С5, требуется подсчитать количество ячеек, значения в которых больше 1500 и меньше 3500.
Решение.
Результат должен быть получен в ячейке C8. Пошаговыми действиями в ячейку C8 следует ввести формулу: =СЧЕТЕСЛИМН(C1:C5;C1:C5;«>1500»;C1:C5;«<3500»). В ячейке C8 получится число 2.
3.1.5 Расчет среднего значения
СРЗНАЧ(Число1;Число2;...) - категория статистических функций. В текущую ячейку возвращается среднее значение для чисел указанного диапазона.
Пример 3.7. В диапазоне ячеек A1:A5 из Примера 3.1. определить среднее значение.
Решение.
Результат должен быть получен в ячейке А8. Пошаговыми действиями в ячейку А8 следует ввести формулу: =СРЗНАЧ(А1:А5). В ячейке А8 получится число 2360.
В Excel также существует встроенная функция для усреднения значений в ячейках, удовлетворяющих определенному критерию -
СРЗНАЧЕСЛИ(Диапазон;Условие;Диапазон_усреднения), (Диапазон_усреднения – может быть не заполнен и в этом случае для усреднения будут использоваться ячейки из области Диапазон).
Пример 3.8. В диапазоне A1:A5 из Примера 3.1. требуется вычислить среднее значение чисел, значение которых больше 1500.
40
Решение.
Результат должен быть получен в ячейке А9. Пошаговыми действиями в ячейку А9 следует ввести формулу: =СРЗНАЧЕСЛИ(А1:А5;«>1500»). В ячейке А9 получится число 3000.
В Excel также существует встроенная функция для усреднения значений в ячейках, удовлетворяющих нескольким критериям -
СРЗНАЧЕСЛИМН(Диапазон_усреднения;Диапазон_условия1;Условие1;Диапазон_условия2; Условие2;….).
Пример 3.9. В диапазоне A1:A5 из Примера 3.1. требуется вычислить среднее значение чисел, значение которых больше 1500 и меньше 3500.
Решение.
Результат должен быть получен в ячейке А10. Пошаговыми действиями в ячейку А10 следует ввести формулу: =СРЗНАЧЕСЛИМН(А1:А5;А1:А5;«>1500»;А1:А5;«<3500»). В ячейке А10
получится число 2750.
3.1.6 Определение максимального значения
МАКС(Число1;Число2;...) - категория статистических функций. В текущую ячейку возвращается максимальное число из данного диапазона.
Пример 3.10. В диапазоне ячеек A1:A5 из Примера 3.1., определить максимальное значение.
Решение.
Результат должен быть получен в ячейке А11. Пошаговыми действиями в ячейку А11 следует ввести формулу: =МАКС(А1:А5). В ячейке А11 получится число 3500.
3.1.7 Определение минимального значения
МИН(Число1;Число2;...) - категория статистических функций. В текущую ячейку возвращается минимальное число из данного диапазона.
Пример 3.11. В диапазоне ячеек С1:С5 из Примера 3.3., определить минимальное значение.
Решение.
Результат должен быть получен в ячейке С9. Пошаговыми действиями в ячейку С9 следует ввести формулу: =МИН(С1:С5). В ячейке С9 получится число 1500.
3.1.8 Генерация случайного числа
СЛЧИС() - категория математических функций. В текущую ячейку возвращается равномерно распределенное случайное вещественное число, большее либо равное 0 и меньшее 1. Чтобы получить случайное вещественное число на отрезке a и b, необходимо использовать формулу:
СЛЧИС()*(b-a)+a.
С помощью функции СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница) можно генерировать целые числа на интервале, ограниченном нижней и верхней границей.
Случайное число генерируется при каждом вычислении рабочего листа. Чтобы сгенерированные случайным образом числа не меняли свои значения в дальнейшем, необходимо при окончании введения формулы нажать F9. Если это не одна ячейка, а диапазон ячеек с генерирующимися значениями, необходимо выделить этот диапазон и вставить его, используя
контекстное меню и команды СПЕЦИАЛЬНАЯ ВСТАВКА/ВСТАВИТЬ ЗНАЧЕНИЯ.
Пример 3 .12. Сгенерируйте вещественные и целые случайные числа для интервала (0:20).
Решение.
Для решения используются формулы СЛЧИС()*20 и СЛУЧМЕЖДУ(0;20) соответственно.
41
Самостоятельно получите случайным образом вещественные и целые числа, ограниченные отрезком от 50 до 100.
3.1.9Функции прогнозирования
ВMS Excel имеются функции, выполняющие роль инструмента регрессионного анализа, которые позволяют строить линии тренда без создания диаграммы. Эти функции находятся в категории статистических функций, но мы рассмотрим две функции ТЕНДЕНЦИЯ и РОСТ. Отличаются они тем, что функция ТЕНДЕНЦИЯ позволяет строить линии тренда вне диаграммы на основе линейной регрессии, а РОСТ на основе экспоненциальной регрессии. Выбор той или иной функции зависит от того, какой тренд – линейный или экспоненциальный более точно подходит для набора данных.
ТЕНДЕНЦИЯ(Известные_значения_y;Известные_значения_x;Новые_значения_x;Конст) -
категория статистических функций. В текущую ячейку возвращается Новые_значения_х, рассчитанные на основании известных значений. Аргумент Конст является необязательным.
Пример 3.13. Ввести таблицу, начиная с ячейки G1:
Год |
Цена |
Спрос |
|
|
|
2011 |
530 |
1000 |
|
|
|
2012 |
400 |
1150 |
|
|
|
2013 |
615 |
1300 |
|
|
|
2014 |
|
|
|
|
|
2015 |
|
|
|
|
|
2016 |
|
|
|
|
|
Таблица 2.2. Тенденция
Решение.
Результат прогнозирования должен быть получен в ячейке H5. Пошаговыми действиями для вычисления прогноза цены в ячейку H5 вводим формулу: =ТЕНДЕНЦИЯ(H2:H4;G2:G4;G5), аналогично вычисляем прогноз для спроса. В ячейке H5 и I5 соответственно получатся значения 600
и 1450.
Самостоятельно рассчитайте цену и спрос для 2015 и 2016 годов.
РОСТ(Известные_значения_y;Известные_значения_x;Новые_значения_x;Конст) -
категория статистических функций. В текущую ячейку возвращается Новые_значения_х, рассчитанные на основании известных значений.
Предыдущий пример решите аналогичным образом с помощью функции РОСТ и полученные результаты сравните.
3.1.10 Определение ранга числа
РАНГ(Число;Ссылка) - категория статистических функций. Функция вычисляет ранг числа, в списке чисел, т.е. его порядковый номер относительно других чисел, указанных в списке.
Пример 3 .14. Для каждой ячейки из диапазона D1:D5 определить ранг числа.
Решение.
В ячейки D1, D2, D3, D4, D5 введем числа 1000; 800;900;1500;2000 соответственно Результат должен быть получен в ячейках E1:E5. Функция ранга вводится сначала в ячейку E1, затем копируется для всех ячеек до E5. Пошаговыми действиями Мастера функций в ячейку E1 вводим формулу: =РАНГ(D1;$D$1:$D$5) - знак $ устанавливает абсолютные адреса, чтобы диапазон ячеек не менялся при копировании.
После копирования формулы для ячеек E2:E5, получим ранги для каждого значения
42

диапазона – 3; 5; 4; 2; 1. . Ранг числа с максимальным значением в диапазоне D1:D5 будет равен 1, а с минимальным равен 5.
3.1.11 Определение процентной нормы числа
ПРОЦЕНТРАНГ(Массив;Х) - категория статистических функций. Функция вычисляет процентную долю числа, заданного адресом ячейки от максимального значения в указанном массиве. Действие функции аналогично функции РАНГ, только ранг определяется в процентном отношении (максимальное число принимается за 100%, минимальное – за 0%).
Пример 3.15. Для значений ячеек D1, D2, D3, D4, D5 определить процентную долю каждого числа от максимального значения в диапазоне.
Решение.
В ячейки D1, D2, D3, D4, D5 введем числа 1000; 800;900;1500;2000 соответственно. Результат должен быть получен в ячейках F1:F5. Для этого в ячейку F1 введем формулу =ПРОЦЕНТРАНГ($D$1:$D$5;D1). Скопируем эту формулу в ячейки F2, F3, F4, F5. В результате получим числа 50%; 0%; 25%; 75%; 100% (для этих ячеек задайте процентный формат).
3.1.12 Функции для работы с матрицами
МОБР(Массив) - категория математических функций. Вычисляет в выделенном диапазоне обратную матрицу для матрицы, хранящейся в массиве1.
Массив - это числовой массив с равным количеством строк и столбцов. Массив может быть задан как диапазон ячеек, например, A1:В2 или как имя диапазона или массива. Если какая-либо из ячеек в массиве пуста или содержит текст, а также, если массив имеет неравное число строк и столбцов, то функция МОБР возвращает значение ошибки #ЗНАЧ!.
Пример 3.16. Создать новый лист «Функции для работы с матрицами», в ячейки А1:В2 ввести матрицу:
2 |
5 |
||
|
1 |
3 |
|
|
|
||
Требуется найти матрицу, обратную данной.
Решение.
Результат должен быть получен в диапазоне ячеек А4:В5. Выделить диапазон, в который будет помещена матрица, обратная данной. В выделенный диапазон ввести формулу: =МОБР(А1:В2), ввод формулы завершить нажатием клавиш «Ctrl»+«Shift»+«Enter». В результате получим матрицу
3 |
5 |
||
|
1 |
2 |
|
|
|
||
МОПРЕД(Массив) - категория математических функций. Вычисляет определитель матрицы (матрица хранится в массиве).
Определитель матрицы - это число, вычисляемое на основе значений элементов массива2. В данном случае массив - это числовой массив с равным количеством строк и столбцов. Если какая-либо ячейка в массиве пуста или содержит текст, то функция МОПРЕД возвращает значение ошибки #ЗНАЧ!. МОПРЕД также возвращает значение ошибки #ЗНАЧ!, если массив имеет
1 Исходная матрица: |
a |
b |
Обратная матрица: |
d/(a*d-b*c) |
b/(b*c-a*d) |
|
с |
d |
|
c/(b*c-a*d) |
a/(a*d-b*c) |
2 Для некоторого массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом: МОПРЕД(A1:C3) равняется A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1).
43
неравное количество строк и столбцов.
Пример 3.17. Для матрицы из Примера 3.16. найти определитель.
Решение.
В ячейку А7 введем формулу: =МОПРЕД(А1:В2). Нажмем ОК. Получим число 1.
МУМНОЖ(Массив1;Массив2) - категория математических функций. Вычисляет произведение матриц, хранящихся в массивах 1 и 2.
Для того, чтобы можно было вычислить произведение матриц, должно выполняться следующее условие – количество столбцов в Массиве1 должно быть равным количеству строк в Массиве2. Если размерность матрицы Массив1 m n, а матрицы Массив2 n r, то в результате произведения получится матрица размерностью m r, где каждый элемент будет равен сумме произведений элементов i-й строки матрицы Массив1 на соответствующие элементы j-го столбца
|
n |
матрицы Массив2: cij ai1 b1 j ai 2 b2 j K ain bnj |
aik bkj , где i = 1, 2, …, m; j = 1, 2, …, r. |
|
k 1 |
Если хотя бы одна ячейка в матрицах пуста или содержит текст, то функция МУМНОЖ возвращает значение ошибки #ЗНАЧ!.
2x y z 5
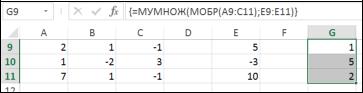
Пример 3.18. Найти решение системы линейных уравнений x 2 y 3z 3 .
7x y z 10
Решение.
Результат должен быть получен в диапазоне ячеек G9:G11, следующим образом:
1.В диапазон A9:C11 введите значения при неизвестных.
2.В диапазон Е9:Е11 введите значения результатов каждого из уравнений.
3.Выделите диапазон G9:G11 и введите формулу =МУМНОЖ(МОБР(А9:С11);Е9:Е11). Ввод формулы завершить нажатием комбинацией клавиш «Ctrl»+«Shift»+«Enter» (рис. 3.1).
Рис. 3.1. Решение уравнений с помощью метода обратной матрицы
В диапазоне G9:G11 получим значения 1, 5 и 2, т.е. x=1, y=5 и z=2. Подставив в любое из уравнений полученные результаты, сделайте проверку.
Решение системы линейных уравнений A*X=B, когда количество уравнений равно количеству неизвестных (m = n), было рассмотрено выше. Однако это является частным случаем, и возможны случаи, когда m не равно n, а именно: m > n, m < n.
В случае, когда m < n и система линейных уравнений является совместной, она не определена и имеет бесконечное множество решений.
Если m > n и система линейных уравнений совместна, то матрица А имеет по крайней мере m – n линейно независимых строк. В данном случае решение можно получить выбором n любых линейно независимых уравнений. Использовав формулу X = A-1 B, можно найти решение данной системы, но на практике применяется более общий подход – метод наименьших квадратов. В этом случае обе части уравнения умножаются на матрицу Ат (Ат – транспонированная матрица А). Затем обе части умножаются на выражение (Ат А)-1 при условии, что это матрица существует и система определена. После некоторых
44
математических преобразований формула решения системы линейных уравнений методом наименьших квадратов примет следующий вид: X (Aт A) 1 Aт B .
Технологию решения систем линейных уравнений методом наименьших квадратов рассмотрим на следующем примере.
8x 5 y 10
Пример 3.19. Решить систему линейных уравнений 5x 2 y 4 .
7x 4 y 8
Решение.
Результат должен быть получен в диапазоне ячеек С29:С30, следующим образом:
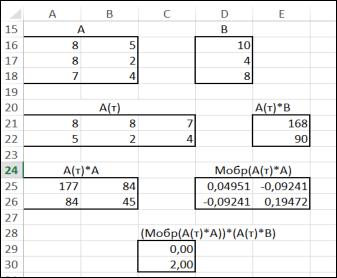
•введем значения элементов матриц А и В в диапазоны рабочего листа, обозначим эти области именами соответственно А и В.
•транспонируем матрицу А, для чего выделим диапазон ячеек размерностью 3 2 и с помощью формулы = ТРАНСП(А) вычислим транспонированную матрицу АТ.
•далее вычислим произведение Ат В с помощью функции МУМНОЖ(Ат;В), предварительно проверив условие умножения матриц.
•следующим шагом является вычисление произведения матриц Ат А.
•далее вычислим матрицу, обратную матрице, полученной в ходе выполнения предыдущего пункта, использовав встроенную функцию МОБР(Ат А).
•последним шагом в данном примере является вычисление произведения матрицы (в соответствии с правилами умножения матриц), полученной в ходе выполнения предыдущего пункта и матрицы полученной в ходе выполнения пункта 3, таким образом, получим выражение МУМНОЖ(МОБР(Ат А);МУМНОЖ(Ат;В)), что и будет являться решением данной системы линейных уравнений (рис. 3.2.).
Рис. 3.2. Решение систем линейных уравнений методом наименьших квадратов
3.1.13 Операции с массивами и матрицами
Электронная таблица Excel позволяет решать задачи с использованием массивов различной размерности: одномерные, двумерные и трехмерные. Одномерные и двумерные массивы хранятся на одном листе рабочей книги, а трехмерный массив размещается в одноименных областях смежных листов рабочей книги.
45

С массивами, содержащими числовые данные, можно выполнять различные арифметические операции, в которых участвуют:
•элементы массива и число, например почленное умножение;
•элементы двумерного массива и элементы одномерного массива (вектора), например почленно-построчное умножение;
•массивы различной размерности и т.д.
Для выполнения арифметических операций (сложение, вычитание, умножение, деление и т.д.) над элементами массива требуется:
•выделить область для размещения результата в соответствии с условием задачи;
•в строку формул после знака «равно» вести соответствующее арифметическое выражение;
•закончить ввод формулы комбинацией клавиш «Ctrl»+«Shift»+«Enter», означающей, что результат выполнения данной формулы располагается в диапазоне ячеек.
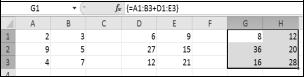
Для вычисления суммы векторов необходимо последовательно выполнить следующие операции:
•в диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора;
•выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы;
•ввести в выделенный диапазон формулу сложения диапазонов =
Адрес_Вектора_1+Адрес_Вектора_2;
•нажать комбинацию клавиш «Ctrl»+«Shift»+«Enter» (рис. 3.3).
Рис. 3.3. Вычисление суммы векторов
Для умножения массива на число в электронной таблице необходимо выполнить следующие операции:
•в диапазоны ячеек ввести значения числовых элементов массива;
•выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходный массив;
•ввести в выделенный диапазон формулу умножения диапазона на число: =
Адрес_Вектора 3;
•нажать комбинацию клавиш «Ctrl»+«Shift»+«Enter» (рис.3.4).
Рис. 3.4. Умножение массива на число Сумма произведений соответствующих координат векторов называется скалярным
произведением векторов и вычисляется с помощью формулы a b a1 b1 a2 b2 K an bn . Для вычисления скалярного произведения векторов необходимо:
46
•в диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора;
•выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные диапазоны;
•ввести в выделенный диапазон формулу перемножения диапазонов =
Адрес_Вектора_1 Адрес_Вектора_2;
•нажать комбинацию клавиш «Ctrl»+«Shift»+«Enter»;
•просуммировать содержимое ячеек диапазона, в котором размещен результат умножения диапазонов.
СУММПРОИЗВ(Массив1; Массив;…) - категория математических функций. Позволяет вычислить в Excel скалярное произведение.
Массив, значения элементов которого записаны в двумерной области, представляет собой двумерную матрицу. Умножение двумерной матрицы на число аналогично операции умножения массива на число, описанной выше.
Суммировать матрицы (векторы) и находить их разность можно только в том случае, если они имеют одинаковую размерность. Матрицы (векторы) складываются (вычитаются) поэлементно.
Например, требуется найти матрицу С, полученную в результате суммирования матриц А и В. Для этого необходимо выполнить следующие действия:
•выделить диапазон, где будут размещаться элементы матрицы С, полученной в результате суммирования матриц А и В;
•в выделенный диапазон ввести формулу = Адрес_Матрицы_1+Адрес_Матрицы_2;
•нажать комбинацию клавиш «Ctrl»+«Shift»+«Enter» (рис. 3.5).
Рис. 3.5. Сложение матриц Аналогичным образом вычисляются разность, скалярное произведение и деление матриц.
ТРАНСП(Массив) - категория функций «ссылки и массивы», позволяющая транспонировать матрицы.
Транспонирование матрицы – процесс перестановки элементов матрицы, когда элементы строк матрицы становятся элементами ее столбцов и наоборот, т.е. если матрица имела размерность m n до транспонирования, полученная матрица будет иметь размерность n m.
Рассмотрим операцию транспонирования матрицы. Требуется транспонировать матрицу Массив размерности m n, для этого необходимо выполнить следующие действия:
•выделить диапазон с размерность n m;
•в выделенный диапазон ввести формулу ТРАНСП(Массив).
3.1.14Функции даты и времени
3.1.14.1 Функция текущей даты
СЕГОДНЯ() – возвращает системную дату текущего компьютера, в формате число, месяц, год.
3.1.14.2 Функция текущей даты и времени
ТДАТА() - возвращает системную дату и время текущего компьютера, в формате число, месяц,
47
год, час, минуты.
3.1.14.3 Функция определения дня недели
ДЕНЬНЕД(Дата_в_числовом_формате;Тип) - преобразует дату в числовом формате в номер дня недели от 1 до 7. Если Тип не указан или равен 1, то первым днем недели считается воскресенье, последним (7-м) - суббота. Если Тип равен 2, первый день недели - понедельник.
Пример 3.20. Определите день недели даты Вашего рождения.
Создайте новый лист и назовите его «Функции даты и времени». В ячейку А1 введите дату рождения, в ячейку В1 введите функцию =ДЕНЬНЕД(А1;2).
Например, первый полет в космос Ю.А. Гагарина был совершен в среду.
3.1.14.4 Функция определения номера месяца
МЕСЯЦ(Дата_в_числовом_формате) - преобразует дату в числовом формате в номер месяца.
В качестве аргумента может быть ссылка на любую ячейку, содержащую дату. Например,
=МЕСЯЦ(А1) или =МЕСЯЦ(ТДАТА()).
3.1.14.5 Функция определения количества дней между двумя датами
ДНЕЙ360(Нач_дата;Кон_дата;Метод) - количество дней определяется как разница между начальной и конечной датами, исходя из 360 дней в году. Метод - задает использование европейского стандарта (необязательный параметр).
Пример 3.21. Определить количество дней от даты Вашего рождения по текущую дату.
Решение.
В ячейку А3 введите формулу =ДНЕЙ360(А1;СЕГОДНЯ()). Следует напомнить, что полученное число будет неточное, поскольку данная функция вычисляет разность исходя из 360 дней в году.
Для более точного определения количества дней следует вычислить разность двух ячеек, в которых находятся соответствующие даты и задать для ячейки с формулой числовой формат. Например, =СЕГОДНЯ()-А1.
Существует функция РАЗНДАТ(Нач_дата;Кон_дата;Тип) которая позволяет вычислять разность в днях, месяцах и годах между двумя датами. Значениеми поля Тип соответственно могут выступать параметры «d»-дни, «m»-месяцы и «y»-года. Следует заметить, что в диалоговом окне ВСТАВИТЬ ФУНКЦИЮ в списке функций такая функция отсутствует, ее необходимо набирать с клавиатуры в соответствии с ее синтаксисом.
3.1.15 Логические функции
3.1.15.1 Функция проверки условия
ЕСЛИ(Лог_выражение;Значение_если_истина;Значение_если_ложь) - категория логических функций.
Лог_выражение – предполагает выполнение операции сравнения, с помощью логических операторов: =, >, <, >=, <= и т.д.
В результате вычисления данной функции получим величину, вычисленную по формуле, содержащейся в поле Значение_если_истина, если Лог_выражение (одно или несколько) истинно, в противном случае, в результате получим величину, вычисленную по формуле, содержащейся в поле Значение_если_ложь.
Создайте новый лист и назовите его «Функции проверки условия».
Пример 3.22. Скопируйте в ячейки А1:А5 информацию из диапазона А1:А5 листа «Математические функции».
48
Решение.
В зависимости от значений в ячейках диапазона А1:А5 выполнить: если значение больше 1000, делим его на 100, если нет - делим на 10. Результат должен быть получен в ячейках В1:В5.
Функция вводится сначала в ячейку В1, затем копируется для всех ячеек до В5. В ячейку В1
вводим формулу =ЕСЛИ(А1>1000;А1/100;А1/10).
3.1.15.2 Использование функции И
Логические функции И и ИЛИ предназначены для проверки выполнения нескольких условий:
1.Когда логические значения соединены логическим И, результатом проверки нескольких логических значений считается: значение ИСТИНА, если все логические значения имеют значение ИСТИНА; значение ЛОЖЬ, если хотя бы одно логическое значение имеет значение ЛОЖЬ.
2.Когда логические значения соединены логическим ИЛИ, результатом проверки логических значений считается: значение ИСТИНА, если хотя бы одно из логических значений имеет значение ИСТИНА; значение ЛОЖЬ, если все логические значения имеют значение ЛОЖЬ.
ЕСЛИ(И(Лог_значение1;Лог_значение2);Значение_если_истина;Значение_если_ложь).
Вычисление Значение_если_истина выполняется только при истинности всех указанных логических значений, в противном случае вычисляется Значение_если_ложь.
Пример 3.23. Для каждого из значений ячеек диапазона А1:А5 из Примера 3.1. проверить условие: если значение ячеек больше 900 и одновременно меньше 1500, то умножить его на 100, в противном случае оставить значение ячейки неизменным.
Решение.
Результат должен быть получен в ячейках С1:С5.
В ячейку С11 ввести: =ЕСЛИ(И(А11>900;А11<1500);А11*100;А11).
Сначала вызывается функция ЕСЛИ, затем из списка встроенных функций в левой части строки формул вызывается функция И для ввода логических условий. После завершения ввода условий в соответствующие поля функции И, следует щелкнуть указателем мыши в конце строки формулы и продолжить ввод значений в окне ЕСЛИ.
Из ячейки C1 формулу скопировать вниз до ячейки С6.
3.1.15.3 Использование функции ИЛИ
ЕСЛИ(ИЛИ(Лог_значение1;Лог_значение2);Значение_если_истина;Значение_если_ложь).
В случае истинности одного из условий (Лог_значение1 или Лог_значение2) вычисляется выражение, находящееся в поле Значение_если_истина, в противном случае вычисляется выражение по полю Значение_если_ложь.
Пример 3.24. Для каждого значения из ячеек диапазона А1:А5 из Примера 3.1 проверить: если значения в ячейках больше или меньше 1000, то умножить их на 10, в противном случае (если равно 1000) оставить значение ячеек неизменным.
Решение.
Результат должен быть получен в ячейках D1:D5.
В ячейку D11 вводим: =ЕСЛИ(ИЛИ(А11>1000;А11<1000);А11*10;А11).
Сначала вызывается функция ЕСЛИ, затем их списка встроенных функций в левой части строки формул вызывается функция ИЛИ для ввода логического условия. После завершения ввода
49
