Алгоритм вычисления обратной матрицы.

1. Находим определитель исходной матрицы. Если , то матрица- вырожденная и обратной матрицыне существует. Если, то матрицаневырожденная и обратная матрица существует.

2. Находим матрицу , транспонированную к.

3. Находим алгебраические дополнения элементов и составляем из них присоединенную матрицу.

4. Составляем обратную матрицу по формуле    .

5. Проверяем правильность вычисления обратной матрицы , исходя из ее определения:.

Пример. Найти матрицу, обратную данной: .

Р е ш е н и е.

1)    Определитель матрицы

.

2)   Находим алгебраические дополнения элементов матрицы и составляем из них  присоединенную матрицу :

.

3)              Вычисляем обратную матрицу:

,

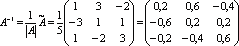4)              Проверяем:

.

№4 Ранг матрицы. Линейная независимость строк матрицы

Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.

В матрице размеромвычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы-го порядка, где. Определители таких подматриц называютсяминорами -го порядка матрицы.

Например, из матриц можно получить подматрицы 1, 2 и 3-го порядка.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение:или.

Из определения следует:

1) Ранг матрицы не превосходит меньшего из ее размеров, т.е..

2) тогда и только тогда, когда все элементы матрицы равны нулю, т.е..

3) Для квадратной матрицы n-го порядка тогда и только тогда, когда матрица- невырожденная.

Поскольку непосредственный перебор всех возможных миноров матрицы , начиная с наибольшего размера, затруднителен (трудоемок), то пользуются элементарными преобразованиями матрицы, сохраняющими ранг матрицы.

Элементарные преобразования матрицы:

1)   Отбрасывание нулевой строки (столбца).

2)   Умножение всех элементов строки (столбца) на число .

3)   Изменение порядка строк (столбцов) матрицы.

4)   Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5)   Транспонирование матрицы.

Определение. Матрица , полученная из матрицыпри помощи элементарных преобразований, называется эквивалентной и обозначаетсяА В.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Матрица называется ступенчатой если она имеет вид:

, где ,,.

Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк , т.к. имеется минор-го порядка, не равный нулю:

.

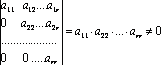Пример. Определить ранг матрицы с помощью элементарных преобразований.

 .

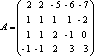
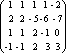
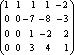
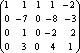
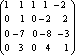
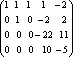
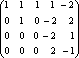
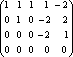
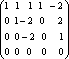Ранг матрицы равен количеству ненулевых строк, т.е. .

№5Линейная независимость строк матрицы

Дана матрица размера

Обозначим строки матрицы следующим образом:

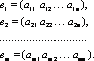
Две строки называются равными, если равны их соответствующие элементы. .

Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно:

.

Определение. Строка называется линейной комбинацией строкматрицы, если она равна сумме произведений этих строк на произвольные действительные числа(любые числа):

.

Определение. Строки матрицы называютсялинейно зависимыми, если существует такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, где . (1.1)

Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.

Определение. Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты , то строкиназываютсялинейно независимыми.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы).

Теорема играет принципиальную роль в матричном анализе, в частности, при исследовании систем линейных уравнений.

№6 Решение системы линейных уравнений снеизвестными

Системы линейных уравнений находят широкое применение в экономике.

Система линейных уравнений спеременными имеет вид:

,

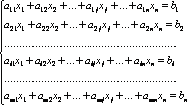где () - произвольные числа, называемыекоэффициентами при переменных и свободными членами уравнений, соответственно.

Краткая запись: ().

Определение. Решением системы называется такая совокупность значений , при подстановке которых каждое уравнение системы обращается в верное равенство.

1)             Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

2)             Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

3)             Две системы уравнений называются равносильными (эквивалентными), если они имеют одно и то же множество решений (например, одно решение).