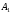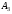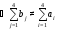Задача 3. Решить транспортную задачу средствамиMsExcel

На трех станциях отправления имеется соответственно 30, 50, и 20 ед. однородного груза, который нужно доставить в четыре пункта назначения согласно их потребностям. Эти данные, а также стоимость перевозки единицыгруза от каждой станции отправления к каждому пункту назначения указаны в таблице. Составить план перевозок грузов, чтобы затраты на эти перевозки были минимальными.

Пункты отправления	Запасы груза	Пункты назначения
	30	1	8		2	3
	50	4	7		5	1
	20	5	3		4	4
Потребности		15		35	40	30

Решение.

Часто условие транспортной задачи оформляют матрицей:

1	8	2	3	30
4	7	5	1	50
5	3	4	4	20
15	35	40	30

1. Построим математическую модель транспортной задачи.

1.1. «Составить план перевозок грузов» - значит определитьсколько, от куда и куданадо перевезти груза, чтобы достичь поставленной цели - «затраты на эти перевозки были минимальными». Введем управляющие переменные: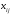- количество груза, перевозимого из пункта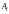в пункт().

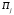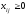1.2.Стоимость этой перевозки составит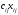. Тогда целевая функция - суммарные затраты, связанные с реализацией всего плана перевозок – запишется выражением:

в общем ви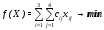де , где

в нашей задаче:

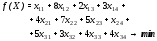
3. Для построения системы ограничений проверим, является ли задача сбалансированной.

Суммарная мощность поставщиков Суммарная мощность потребителей

Следовательно, условие сбалансированности не выполнено.

1.4.Запишем систему ограничений:

По потребителю: мощности поставщиков меньше мощности потребителей, следовательно, кто-то из потребителей получит груза меньше, чем его потребность.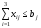

Количество груза, которое потребитель 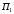действительно получит, запишется выражением: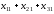. Так как это меньше, чем его потребность, ограничение будет иметь вид:.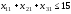

Аналогично строятся ограничения по другим потребителям. Так как в задаче заранее не оговаривается, потребности какого потребителя не будут удовлетворены, знак поставим в ограничениях по всем потребителям. Получим систему ограничений по потребителю:

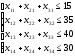
По поставщику:весь имеющийся на станции отправления груз будет вывезен (т.е.):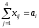

;

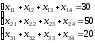Прямые ограничения .

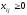2. Подготовим форму для ввода исходных данных и запуска программы Поиск решения

• Оптимальное значение целевой функции будет помещено в ячейке В8:

Мастер функций / Математические / СУММПРОИЗВ(В3:E5;I3:L5)

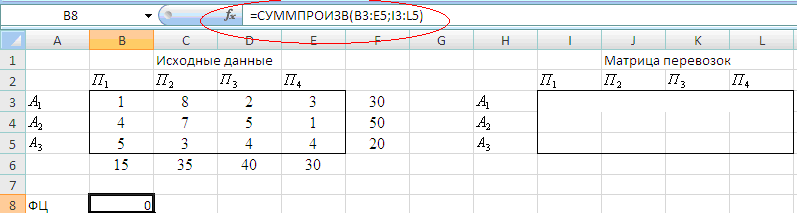
• Введем зависимости ограничений, стоящие в левых частях ограничений.

- вводим условия реализации мощностей поставщиков:

Мастер функций / Математические / сумм(i3:l3)

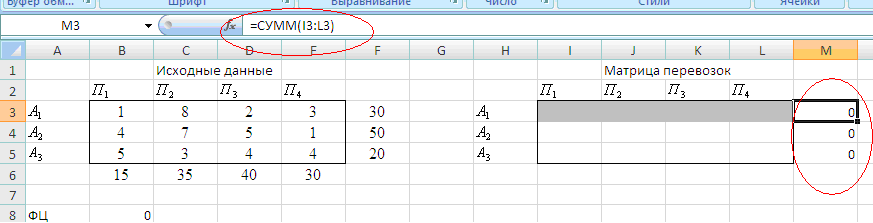
- вводим зависимостей ограничений по потребителям:

Мастер функций / Математические / сумм(i3:i5)

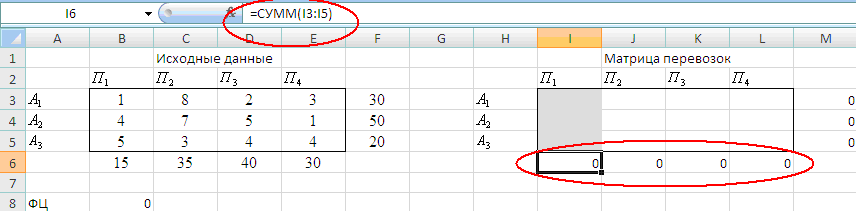
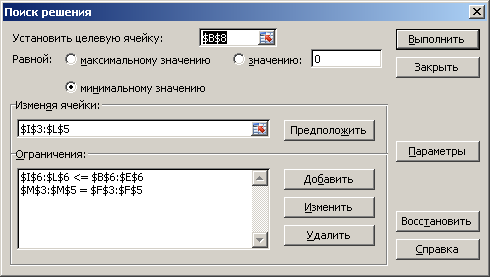
После выбора команд Поиск решенияпоявится диалоговое окно Поиск решения.

Результат поиска решения

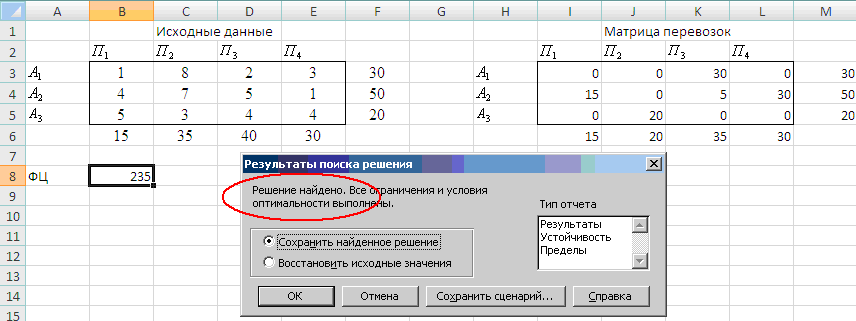
Найденный план перевозок означает, что общая стоимость перевозок составит 235 ден.ед., если

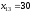ед. груза перевезти со станции 1 потребителю 3;

ед. груза перевезти со станции 2 потребителю 1;

ед. груза перевезти со станции 2 потребителю 3;

ед. груза перевезти со станции 2 потребителю 4;

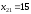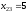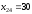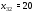ед. груза перевезти со станции 3 потребителю 2.

Неудовлетворен будет потребитель 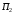, т.к. его потребность составляет 35 ед. груза (ячейкаJ6), а получит он только 20 ед. (ячейка C6). Остальные потребители удовлетворены полностью.