38.​ Примитивно-рекурсивные функции.

39.​ Понятие сложности алгоритма.

Для анализа и/или сравнения алгоритмов между собой необходимо ввести некий критерий качества. Основным критерием качества является сложность. Сложность - это количественная оценка ресурсов, затрачиваемых алгоритмом.

Ресурсы:

•Человеческие (создание и понимание алгоритма). Оценивает интеллектуальная сложность. Единого критерия оценки не существует.

•Вычислительные (на выполнение алгоритма):

•Память. Оценивает пространственная сложность - количество памяти, требующееся для выполнения алгоритма.

•Процессорное время. Оценивает временная сложность - количество времени, необходимое на выполнение алгоритма.

40.​ Комбинаторика. Правила суммы и произведения.

Комбинаторика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Правило суммы. Если некоторый объект может быть выбран из совокупности объектов способами, а другой объект может быть способами, то выбрать либо, либо можно способами.

Правило произведения. Если некоторый объект может быть выбран из совокупности объектов способами и после каждого такого выбора другой объект может быть выбран способами, то пара объектов в указанном порядке может быть выбрана способами.

41.​ Комбинаторика. Принцип включения и исключения.

Формула включений-исключений(илипринцип включений-исключений) —комбинаторнаяформула, позволяющая определить мощностьобъединенияконечного числаконечных множеств, которые в общем случае могутпересекатьсядруг с другом. В теории вероятностей аналог принципа включений-исключений известен как формулаПуанкаре^[1].

Например, в случае двух множеств формула включений-исключений имеет вид:

В сумме элементы пересеченияучтены дважды, и чтобы компенсировать это мы вычитаемиз правой части формулы. Справедливость этого рассуждения видна издиаграммы Эйлера-Веннадля двух множеств

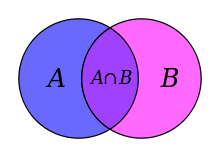
Случай двух множеств

42.​ Бином Ньютона.

Бином Ньютона — Бином Ньютона — формула разложения произвольной натуральной степени двучлена (а+b)n в многочлен.

где -биномиальные коэффициенты,n- неотрицательноецелое число.

43.​ Числа Фибоначчи. Приемы вычисления сумм. Исключить

44.​ Понятие графа. Подграф.

Граф- это конечное множество V, которое называется множество вершин и множество E. Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).

45.​ Степень вершины графа.

Степенью или валентностью вершины называется количество ребер инцидентности этой вершины d(V).

46.​ Маршрут в графе. Цикл в графе.

Маршрутом в графе называется последовательность вершин и ребер v0 v1 v2 v3 …vn.

Замкнутая цепь называется циклом.

47.​ Связность графа.

Граф называется связным, если любые 2 вершины соединены хотя бы одним путём. 54

48.​ Ориентированные и неориентированные графы.

Ориентированный граф или орграф называется граф, у которого множество ребер является множеством упорядоченных пар. Неориентированным графом G(V, E) называется совокупность двух множеств: не пустого множества V (множества вершин) и множества E - множество неупорядоченных пар элементов из V (множества ребер).

49.​ Графы. Задача Эйлера. Цикл Эйлера.

Граф, в котором найдется маршрут, начинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется эйлеровым графом. Последовательность вершин (может быть и с повторениями), через которые проходит искомый маршрут, как и сам маршрут, называется эйлеровым циклом.

50.​ Способы задания графов.

1.Задание графов матрицей смежности

2. Задание графов матрицей инцидентций.

51.​ Матрицы инцидентности и матрица смежности и их применение в теории графов.

Матрица смежности – это квадратная матрица порядка p (количество вершин),  элемент которой,  стоящий в i строке и j столбце определяется по правилу:

Матрицей  инцидентцииназывается прямоугольная матрица размерностиp x q(p – количество вершин,q– количество ребер), элемент которой стоящий вiстроке иjстолбце определяется по правилу:

- для неориентированного графа.

- для ориентированного графа.

52.​ Полный и двудольный графы.

Двудольный граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

Полный - простой граф, в котором каждая пара различных вершин смежна.

53.​ Дерево как частный случай графа.

Связный ацикличный граф G= (V,E) является деревом.

Утверждения о связном графе с nвершинами иmрёбрами эквивалентны:

G– дерево

Любую пару вершин Gсвязывает единственный путь

Gсвязен иm=n-1

Gсвязен, а удаление любого ребра нарушает это свойство.

G– ацикличен, но связываю любую пару вершин новым ребром, мы получаем цикл.

54.​ Понятия инцидентности и валентности в теории графов.

Если вершина vявляется концом ребра х, то говорят, чтоvиxинцидентны.

Степенью вершины v(она же валентность) считают числоm(v) рёбер графа, инцидентныхv.

55.​ Маршрут, цепь и цикл в графе.

Маршрутом длины kв графеGназывается такая последовательность вершинv0,v1,…,vk, что для каждогоI= 1,...,kпараvi– 1viобразует ребро графа.

Циклом в графе принято называть последовательность вершин v0,v1,…,vk, каждая пара которых является концами одного ребра, причёмv0 =v1, а остальные вершины (и рёбра) не повторяются.

Цепь в графе – маршрут, все рёбра которого различны.