Задача 2

Используя построенный в задаче № 1 интервальный ряд распределения предприятий малого бизнеса по стоимости основных фондов, определите:

1. моду и медиану построенного интервального ряда распределения графическим и расчетным методами.

2. характеристики интервального ряда распределения: среднюю арифметическую, среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.

3. среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем, рассчитанным в п. 3 для интервального ряда распределения.

Сделайте выводы по результатам выполнения пунктов 1, 2, 3 задания.

Объясните причину их расхождения.

Решение

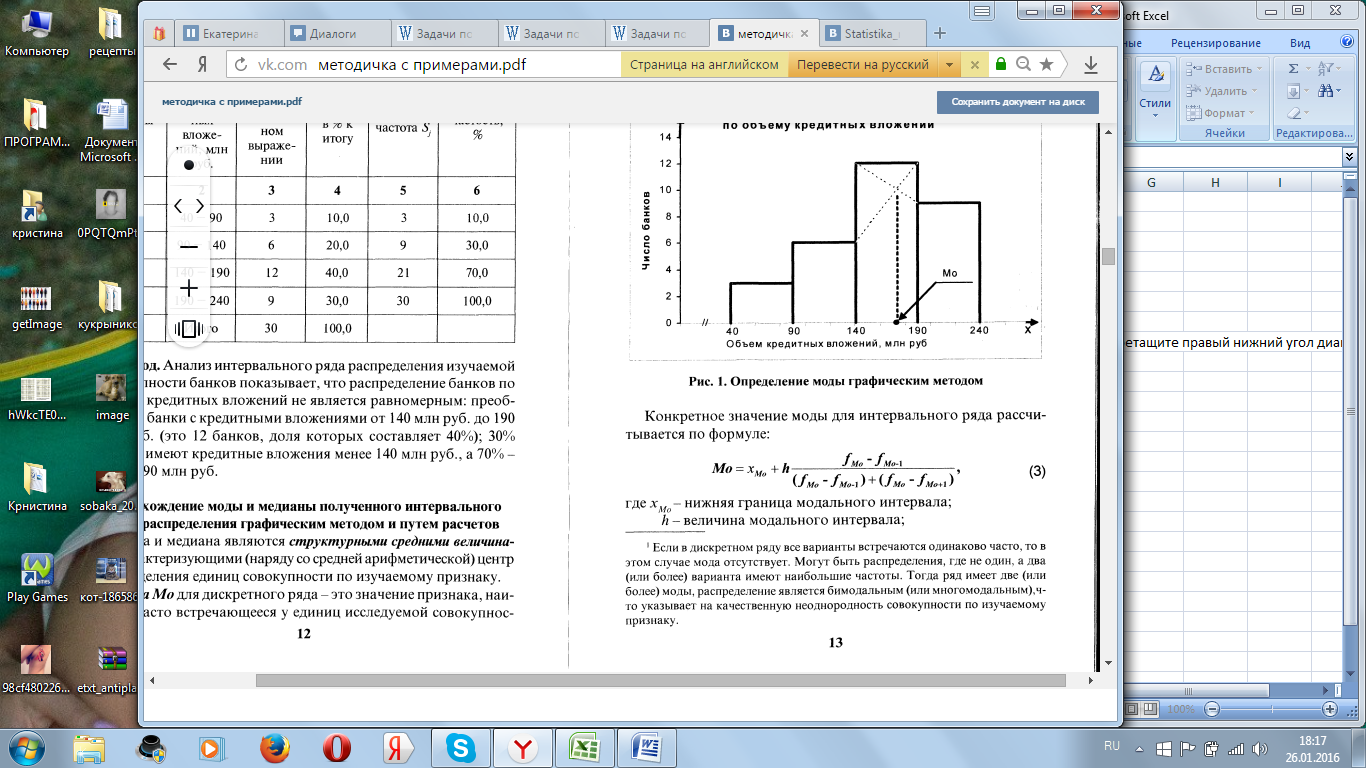
Для определения моды графическим методом построим по данным таблицы гистограмму распределения предприятий по изучаемому признаку.

Рис. 1 Определение моды графическим методом

Конкретное значение моды для интервального ряда рассчитывается по формуле:

(2)

Где -нижняя граница модального интервала

h- величина модального интервала

-частота модального интервала

-частота интервала, предшествующего модальному

-частота интервала следующего за модальным

согласно таблице 3 модальным интервалом построенного ряда является интервал 8,4 – 10,2 так как его частота максимальна (равна 7)

расчет моды по формуле:

=8,4+1,8*=9 (млн. руб.)

Вывод: для рассматриваемой совокупности предприятий наиболее распространенная стоимость основных фондов – 9 млн. руб.

Конкретное значение медианы для интервального ряда рассчитывается по формуле:(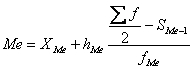3)

Где Х_Ме – нижняя граница медианного интервала;

h_Me – величина медианного интервала;

∑f - сумма частот ряда;

f_Ме – частота медианного интервала;

S_Ме-1 – комулятивная (накопленная) частота интервала, предшествующего медианному.

Таблица 5

Структура предприятий по стоимости основных фондов

№ группы	Стоимость основных фондов (млн. руб.)	Число предприятий		Накопительная частота	Накопительная частность
		В абсолютном выражении	В % к итогу
1	3 – 4,8	2	10	2	10
2	4,8 – 6,6	3	15	5	25
3	6,6 – 8,4	5	25	10	50
4	8,4 – 10,2	7	35	17	85
5	10,2 – 12,0	3	15	20	100
Итого		20	100

Расчет значения медианы по формуле:

=8,4+1,8*=8,4 (млн. руб.)

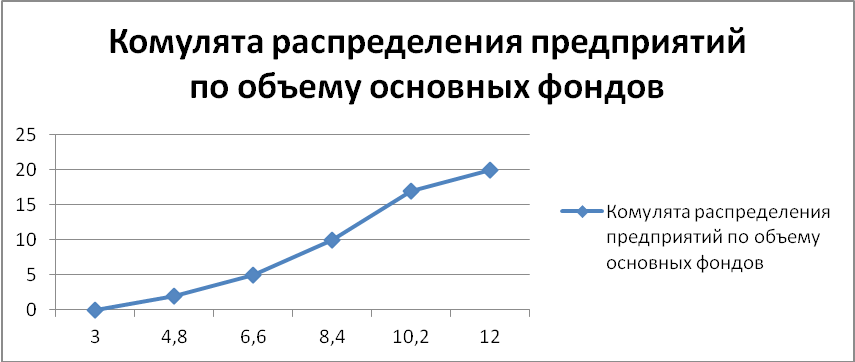
Рис.2 Определение медианы графическим методом

Вывод: В рассматриваемой совокупности предприятий половина имеет стоимость основных фондов не более 8,4 млн. руб., а другая половина не менее 8,4 млн. руб.

Для расчета характеристик ряда распределения строится вспомогательная таблица серединного интервала.

Таблица 6

Расчетная таблица для нахождения характеристик ряда распределения

Группы предприятий по стоимости основных фондов	Середина интервала	Число предприятий	*	-	(-)2	()2*
3 – 4,8	3,9	2	7,8	-4,14	17,1396	34,2792
4,8 – 6,6	5,7	3	17,1	-2,34	5,4756	16,4268
6,6 – 8,4	7,5	5	37,5	-0,54	0,2916	1,4580
8,4 – 10,2	9,3	7	65,1	1,26	1,5876	11,1132
10,2 – 12,0	11,1	3	33,3	3,06	9,3636	28,0908
Итого:		20	160,8			91,368

Расчет средней арифметической взвешенной:

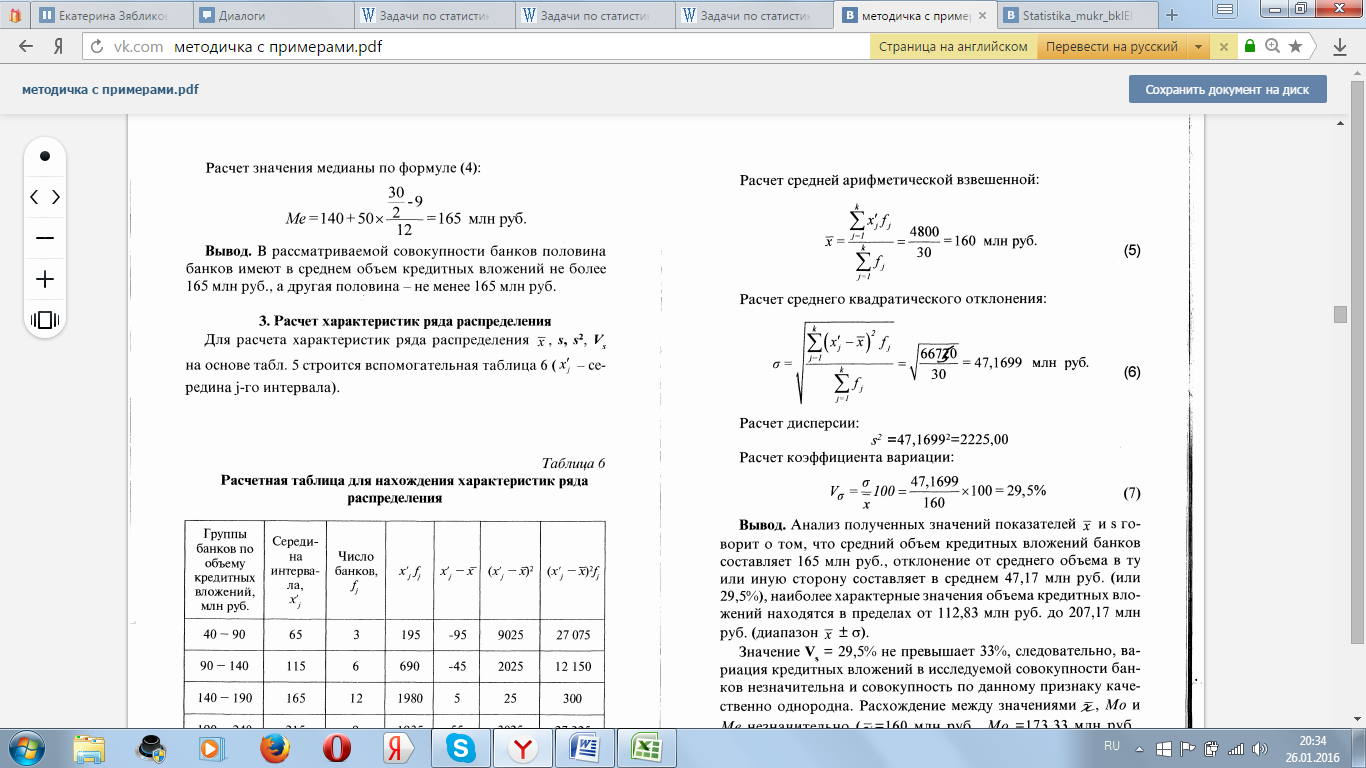(4)

Расчет среднего квадратического отклонения:

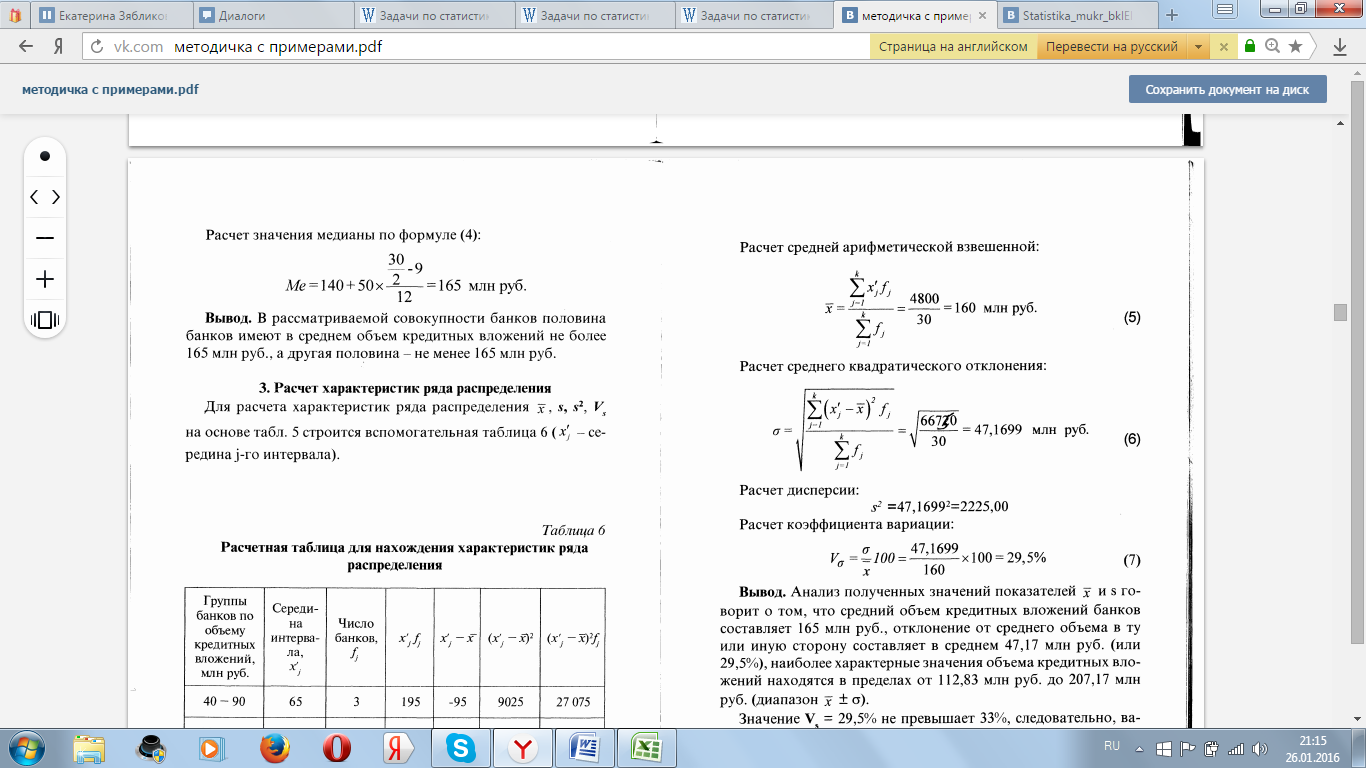(5)

ᵟ ==2,137 (млн. руб.)

Расчет коэффициента вариации:

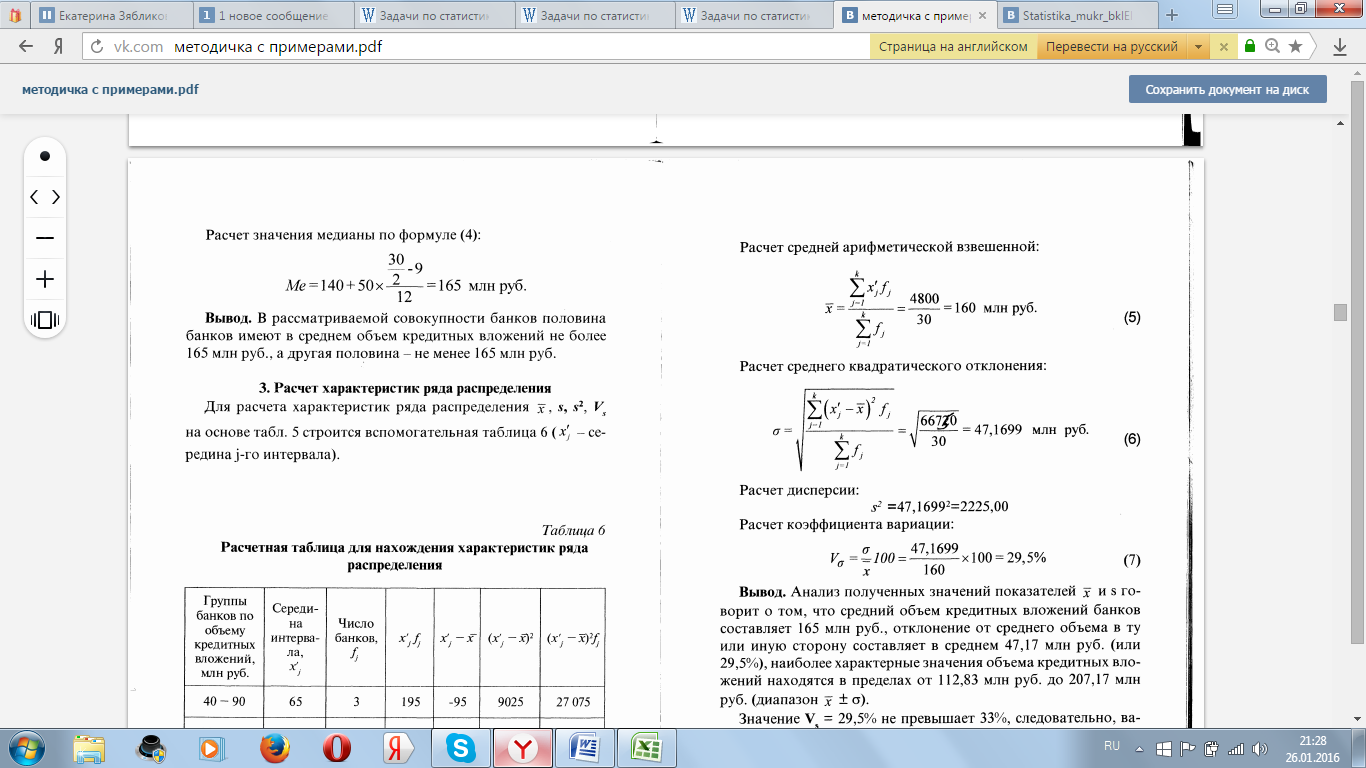(6)

=%

Вывод: Анализ полученных значений показателя , говорит о том, что средняя стоимость основных фондов предприятий составляет 8,04 млн. руб., отклонение от среднего размера в ту или иную сторону составляет в среднем 2,137 млн. руб. (или 26,6%).

Значение =26.6%, не превышает 30%, следовательно вариация стоимости основных фондов в исследуемой совокупности предприятий незначительна и совокупность по данному признаку качественно однородна. Расхождение между , незначительно (8,04; 9; 8,4), что подтверждает вывод об однородности совокупности предприятий. Таким образом, найденное среднее значении торговой площади предприятия 8,04 является надежной характеристикой исследуемой совокупности предприятий.

Вычисление средней арифметической по исходным данным:

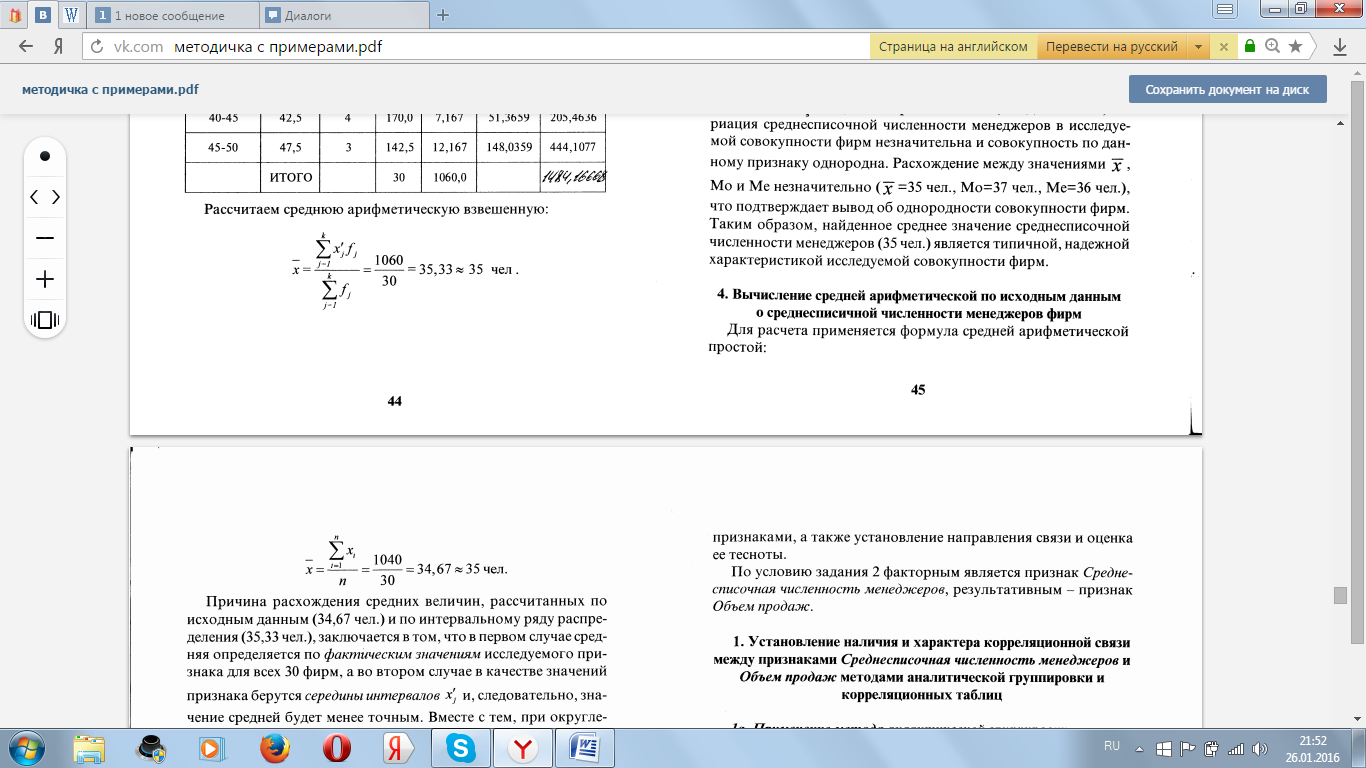(7)

=8,1

Причина расхождения средних величин, рассчитанных по формулам 7 и 4, заключается в том, что по формуле 7 средняя определяется по фактическим значениям исследуемого признака для всех 20 предприятий, а по формуле 4 средняя вычисляется для интервального ряда. Когда в качестве значений признака берутся середины интервалов и, следовательно, значение средней будет мене точным.