matem_voud_1

b = 6 – мнимая ось гиперболы: ; F) 3x² - y² = 9

ВВВВВ пространстве заданы плоскость Ax + By + Cz + D = 0 и прямая .Тогда

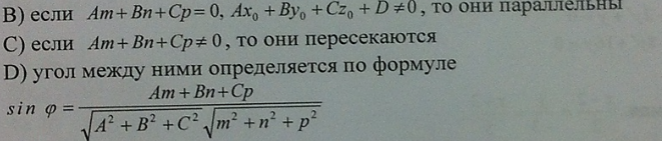
Верное равенство: k x i = j; i x i = 0

Вычислить интеграл : ( )² * 6 ln e ; ( )² * 7

Вычислить интеграл : 2¹ _* ( )²; D) 2² * 3

ДДДДДана матрица А и обратная к ней А^-1 . Тогда: C) А^-1 * А = Е; D) (А^-1 )^-1=А; E) А* А^-1 = Е

Дана неявная функция е^у – е^х + ху = 0. Тогда верной является частная производная

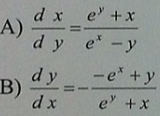
Дана плоскость о – 2y + 3z + 3 = 0: она проходит через точку А (-2; 1; -1); она проходит через точку А (2; 1; -1)

Дана поверхность z = x² - y² + 3, -4х + 2у – 4 и точка М (-1; 0; 1), Тогда: E) , уравнение нормали к данной поверхности в точке М; G) 6х + y + z + 5 = 0, уравнение касательной плоскости к данной поверхности в точке М

Дана функция u (x, y, z) = x² + y² + z² и точка М(1,1,1). Тогда верным является утверждение: E) grad u = 2xi + 2yj + 2zk; F) (du/dz) М = 2

Даны векторы i = (1;0;0), j= (0;1;0), k = (0;0;1) тогда: C) они образуют правую тройку; E) они образуют базис; G) они некомпланарные

Для гиперболы = 1 справедливо утверждение: A) ɛ = 5/4 эксцентриситет

Для определенного интеграла справедливо:

Для площади S фигура ограниченной линиями у² = 9 х, у = 3 х справедливо: B) S = 0.5; E) 0.3 ≤ S ≤ 0.5; G) 0.5 ≤ S ≤ 0.8

Для степенного ряда верно утверждение: B) ; D)

Для числового ряда верно утверждение

ЕЕЕЕЕЕсли a = (x₁; y₁; z₁), b = (x₂; y₂; z₂), то векторное произведение a x b =:

i j k

x₁ y₁ z₁

x₂ y₂ z₂

F) y₁ z₁ x₁ z₁ x₁ y₁

y₂ z - x₂ z_{2 ,} x₂ y₂

ЗЗЗначение определенного интеграла принадлежит промежутку: A) (0; 3); B) (-2; 1)

Значение определенного интеграла принадлежит промежутку: B) (-1; 2)

Значение определенного интеграла принадлежит промежутку: C) (0; 3); E) (-1; 2)

Значение определителя сохранит свое значение, если: элементы всех его столбцов заменить соответствующими сроками; прибавить к элементам ряда соответствующие элементы любого другого параллельного ряда умноженное на один и тот же множитель ƛ≠0; элементы всех его строк заменить соответствующими столбцами

Значение полного дифференциала функции z = х³ + у⁴ в точке Р (1; -2), если Δх = - 0,01, Δу = 0,02, принадлежит промежутку: B) (-1; 2); D) (-3; 0); E) (-2; 1)

Значение предела принадлежит интервалу: B) (0;3); C) (2;5)

Значение предела принадлежит интервалу: A) (-1;2); B) (0; 3); C) (1; 4)

Значение предела принадлежит интервалу: C) (0; 3); D) (-1; 2)

Линейные операции над векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂). В координатной форме: A) (х₁ – х₂; y₁ – y₂; z₁ – z₂); E) (ƛx₁; ƛy₁; ƛz₁); G) (х₁ – х₂; y₁ – y₂; z₁ – z₂)

Матричный метод для решения систем линейных алгебраических уравнений можно применить, если: основная матрица системы невырожденная и ранг основной матрицы равен рангу расширенной матрицы; основная матрица системы невырожденная

Метод Крамера для решения систем линейных алгебраических уравнений можно применить, если C) основная матрица системы невырожденная и ранг основной матрицы равен рангу расширенной матрицы; F) основная матрица системы невырожденная

Один из корней характеристического уравнения равен 0, для дифференциального уравнения: A) y” – y’ = 0; B) y” + 7y’ = 0

Один из экстремумов функции у = 4 + 8х² – х⁴ находится в точке: B) х₀ = -2; C) х₀ = 0; G) х₀ = 2

Одна из асимптот функции задается уравнением: A) х=1; B) у = х; D) х = -1

Одна из координат градиента функции u = 2x² + 3y³ + 4z⁴ точке М (1;-1;0) равна: A) 4

Одна из координат центра сферы x² + y² + z² – 6x + 4z+2 = 0, равна: A) 3; B) -2

Одна из первообразных функции равна: ; ;

Одна из полуосей эллипсоида x² + 9 y² + 4 z² – 36 = 0 равна: A) 6

Одно из первых трех слагаемых разложения функции sin x в ряд Маклорена равно:

Определитель 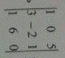равен: C) 47 log ₂ 4 D) 47 ln e² E) 47

Параллельными прямыми являются: A) 2x + 3y – 4 = 0, -4x -6y – 1 = 0; D) y = - 2x + 1, y = 5 – 2x; F) x – 3y +1 = 0, y = 1/3 x – 2

По признаку Даламбера ряд : D) сходится, т.к. q<1, q<1

По радикальному признаку Коши ряд : расходится, т.к. q = е, q = е

По радикальному признаку Коши ряд : расходится, т.к. q>1, q>1; E) расходится, т.к. q = 3, q = 3

Прямая : C) проходит через точку А (2;0;-3); D) параллельна вектору а (2;-3;5); E) перпендикулярна вектору а (2;3;1)

Прямая х – 2у + 1 = 0 проходит через точки: C) (1;1); D) (-1; 0); F) (0, ½)

Прямые заданы уравнениями у_{1 =} k₁ x + b₁ у_{2 =} k₂ x + b₂. Тогда: A) угол между ними определяется по формуле ; C) если k₁ * k₂ = -1, то они перпендикулярны; F) если k₁ = k₂, то они параллельны

Решением дифференциального уравнения y’ – y = 0 является функция: D) y = e^x E) y = C e^x F) y = 0

Система 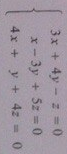совместна; однородная; имеет единственное нулевое решение

Скорость материальной точки в момент времени t=0 равна 2, если перемещение точки выражается функцией: 2 х³ + 2х + 7

Справедливо правило: B) (tg x)’ = 1/cos ² x; F) (arctg x)’ = - 1 / 1 + x²; G) (arcos x)’ =

Функция z = f (x,y), тогда выражение определяет приращение функции: A) Δ _yz = f (x,y + Δ y) – f (x,y) частное приращение z по y; C) Δ _хz = f (х + Δ x,y ) – f (x,y) частное приращение z по х; E) Δz = f (х + Δ x, х + Δ x) – f (x,y) полное приращение z

Функция не имеющая экстремумов: 2 x³ + 5