mat_1805

Көп айнымалы функциялар

$$$ 1

функциясы берілген. нүктесіндегі дербес туындыларының қосындысының мәні:

A)

$$$ 2

функциясының толық өсімшесінің түрі қандай?

A)

$$$ 3

функциясы берілген. нүктесіндегі дербес туындыларының қосындысының мәні:

A) 0

$$$ 4

функциясының толық дифференциалының формуласын көрсетіңіз:

A)

$$$ 5

Егер нүктесі функцияның нүктесіндегі шегі болса, онда

A)

$$$ 6

функциясының деңгей сызығын көрсет

A)

$$$ 7

функциясының нүктесіндегі градиенті деп координаттары ... тең векторды айтады

A)

$$$ 8

функциясы берілген. нүктесіндегі дербес туындыларының қосындысының мәні:

A)

$$$ 9

функциясының нүктесіндегі градиентінің координаттарын тап

A) (5; 2)

$$$ 10

функциясының нүктесіндегі градиентінің координаттарын тап

A) (2; 2)

$$$ 11

функциясының нүктесіндегі градиентінің координаттарын тап

A) (3;-1)

$$$ 12

функциясының нүктесіндегі градиентінің координаттарын тап

A) (-3; 2)

$$$ 13

функциясы экстремум немесе стационар нүктелерінде қандай шартты қанағаттандырады

A)

$$$ 14

функциясының нүктесінде - өзгерісі бойынша алынған дербес өсімшесін тап:

A)

$$$ 15

функциясының нүктесінде аргументі бойынша алынған дербес туындысын көрсет

A)

$$$ 16

функциясының - дербес туындысын тап

A)

$$$ 17

функциясының - дербес туындысын тап

A)

$$$ 18

функциясының - дербес туындысының нүктесіндегі мәнін тап

A) 3

$$$ 19

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 2

$$$ 20

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 3

$$$ 21

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 2

$$$ 22

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 2

$$$ 23

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 6

$$$ 24

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 18

$$$ 25

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 1

$$$ 26

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

A) 0

$$$ 27

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

A) 24

$$$ 28

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

A) 4

$$$ 29

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

A) 12

$$$ 30

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап

A) 24

$$$ 31

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап

A) 60

$$$ 32

функциясының екінші ретті дербес аралас туындысын көрсетіңіз:

A)

$$$ 33

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап

A) 6

$$$ 34

функциясының - екінші ретті аралас туындысының нүктесіндегі мәнін тап

A) 45

$$$ 35

функциясының - екінші ретті аралас туындысының нүктесіндегі мәнін тап

A) 14

$$$ 36

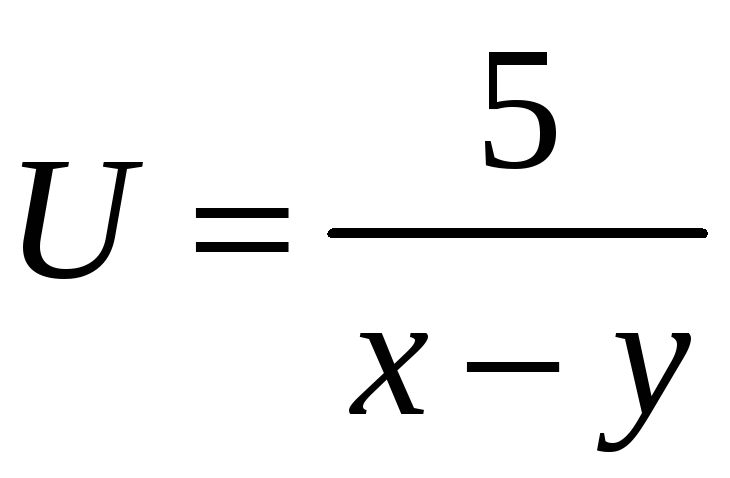функциясының анықталу облысын тап

A)

$$$ 37

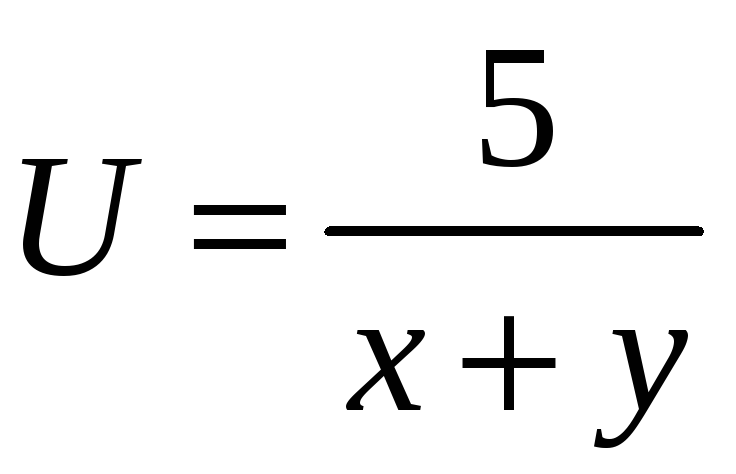функциясының анықталу облысын тап

A)

$$$ 38

функциясының анықталу облысын тап

A)

$$$ 39

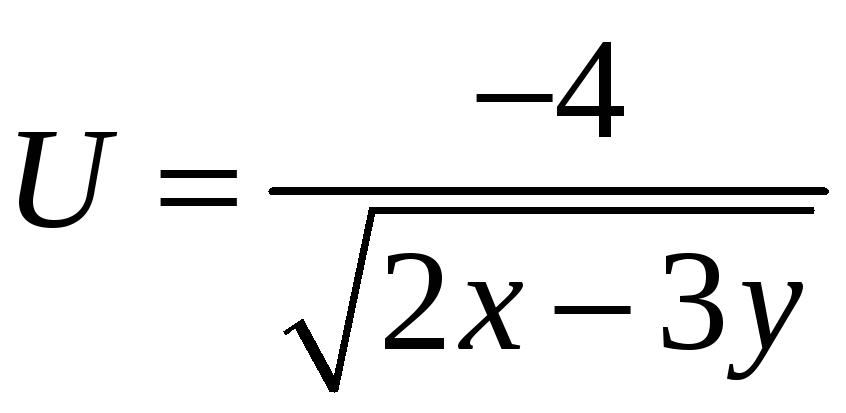функциясының анықталу облысын тап

A)

$$$ 40

функциясының толық дифференциалын табыңыз

A)

$$$ 41

функциясы берілген. Табыңыз :

A) 0

$$$ 42

функциясы берілген. Табыңыз :

A)

$$$ 43

функциясының нүктесіндегі табыңыз

A) 9

$$$ 44

функциясының толық дифференциалын көрсет

A)

$$$ 45

функциясының толық дифференциалын тап

A)

$$$ 46

функциясының толық дифференциалын тап

A)

$$$ 47

функциясының толық дифференциалын тап

A)

$$$ 48

Екі айнымалыдан тәуелді функциясы айқындалмаған түрде берілсе, яғни , онда шартын қанағаттандыратын функциясының х бойынша бірінші ретті дербес туындысын тап

A)

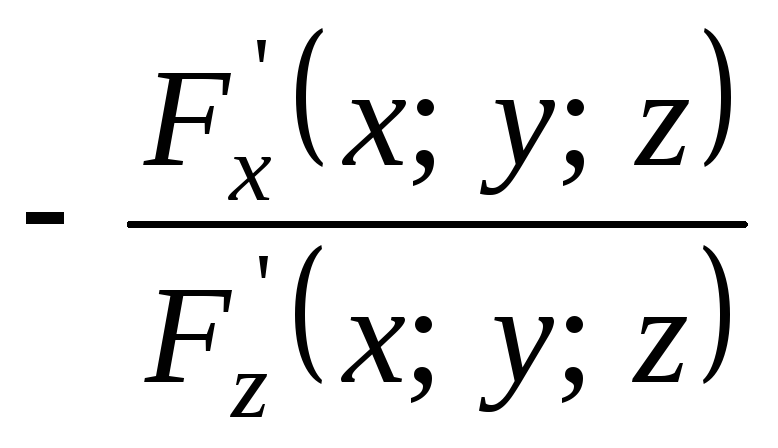
$$$ 49

функциясының - дербес туындысын тап

A)

$$$ 50

функциясының - дербес туындысын тап:

A)

$$$ 51

функциясының - дербес туындысын тап:

A)

$$$ 52

функциясының - дербес туындысын тап

A)

$$$ 53

функциясының - дербес туындысын тап

A)

$$$ 54

функциясының - дербес туындысын тап:

A)

$$$ 55

функциясының - дербес туындысын тап:

A)

$$$ 56

бетінде жататын нүктесі арқылы жүргізілген жанама жазықтықтың теңдеуін көрсет:

A)

$$$ 57

бетіне нүктесі арқылы жүргізілген нормаль түзудің теңдеуін көрсет:

A)

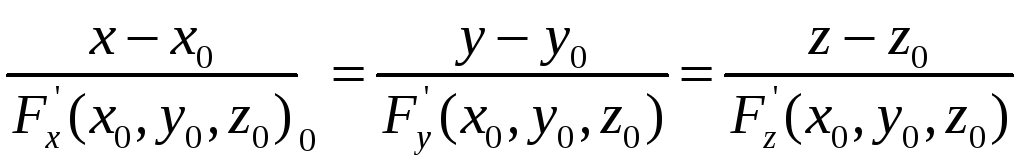
$$$ 58

бетіне нүктесіндегі жанама жазықтықтың теңдеуі былай жазылады:

A)

$$$ 59

Кеңістікте нүктесі арқылы бетіне жүргізілген жанама жазықтықтың теңдеуін тап:

A)

$$$ 60

Кеңістікте нүктесі арқылы бетіне жүргізілген жанама жазықтықтың теңдеуін тап:

A)

$$$ 61

бетінде жататын нүктесі арқылы өтетін нормальдің теңдеуін тап:

A)

$$$ 62

Кеңістікте нүктесі арқылы бетіне жүргізілген нормаль теңдеуді тап:

A)

$$$ 63

Кеңістікте нүктесі арқылы бетіне жүргізілген нормаль теңдеуді тап:

A)

$$$ 64

функциясының нүктесінде төңіректік экстремум болуының жеткілікті шартын көрсет:

A)

$$$ 65

функциясының толық дифференциалын тап

A)

$$$ 66

функциясының толық дифференциалын тап

A)

$$$ 67

функциясының толық дифференциалын тап

A)

$$$ 68

функциясының толық дифференциалын тап

A)

$$$ 69

функциясының экстремумын және сол нүктедегі функцияның мәнін табыңыз

A) нүктесінде

$$$ 70

Екі айнымалы функциясының нүктесінде экстремум болуының қажетті шартын көрсет:

A)

$$$ 71

экстремум нүктесіндегі функцияның мәнін табыңыз

А) нүктесінде

$$$ 72

Екі айнымалы функцияның толық өсімше ұғымына қай формула сәйкес келеді

A)

$$$ 73

Екі айнымалы функцияның - бойынша алынған дербес өсімше ұғымына қай формула сәйкес келеді

A)

$$$ 74

Екі айнымалы функцияның - бойынша алынған дербес өсімше ұғымына қай формула сәйкес келеді

A)

$$$ 75

функциясының экстремумын тап

А) нүктесінде

$$$ 76

функциясының нүктесіндегі - бойынша алынған дербес өсімшесін тап

A)

$$$ 77

функциясының нүктесіндегі - бойынша алынған дербес өсімшесін тап

A)

$$$ 78

- нүктесі кем дегенде екі рет дифференциалданатын функциясының максимум нүктесі болу үшін қандай шарт орындалады

A)

$$$ 79

- нүктесі кем дегенде екі рет дифференциалданатын функциясының минимум нүктесі болу үшін қандай шарт орындалады

A)

$$$ 80

функциясы экстремум немесе стационар нүктелерінде қандай шартты қанағаттандырады

A)

$$$ 81

функциясының - дербес туындысын тап

A)

$$$ 82

функциясының - дербес туындысының нүктесіндегі мәнін тап:

A) 2

$$$ 83

функциясының экстремум нүктелерін тап

A) (2,-2) –максимум нүктесі

$$$ 84

функциясын экстремумге зерттеңіз

A) экстремумы жоқ

$$$ 85

функциясын экстремумге зерттеңіз

A)

$$$ 86

функциясы берілген. Табыңыз :

A) 4

$$$ 87

Кем дегенде екі рет дифференцилданатын функциясының нүктесінде экстремум болмауының шартын көрсет

A)

Екі, үш еселі интегралдар

$$$ 88

Екі еселі интегралдың қасиетін көрсет

A)

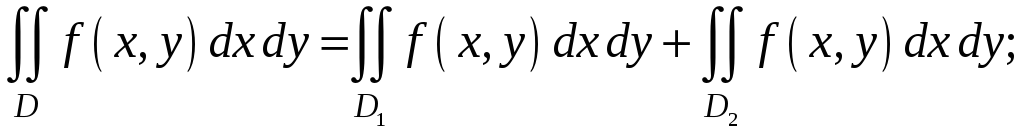
$$$ 89

Екі еселі интегралды тік төртбұрышта есептеу формуласын көрсет

A)

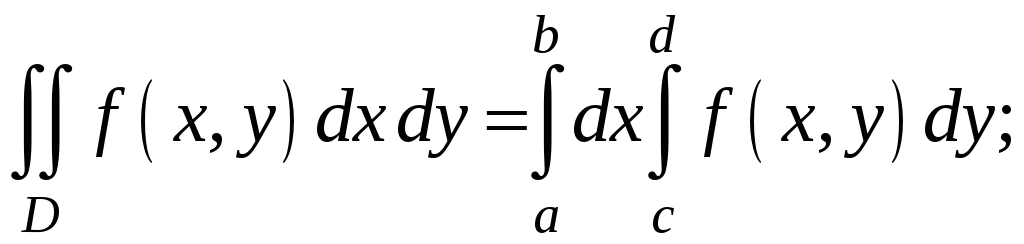
$$$ 90

Екі еселі интегралды облыста есептеу формуласын көрсет: A)

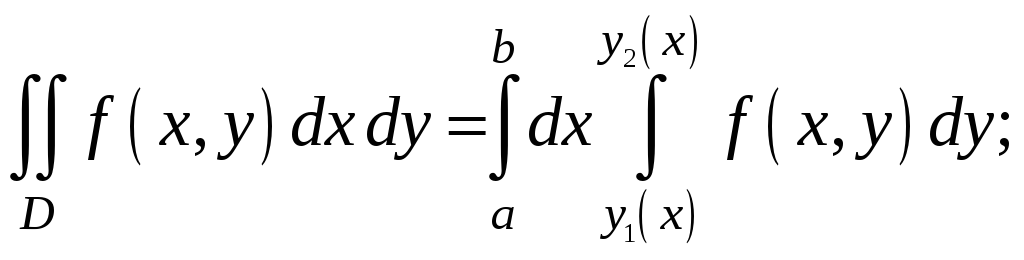
$$$ 91

Екі еселі интегралды декарт координат жүйеден поляр координат жүйеге көшу форуласын көрсет: A)

$$$ 92

Егер поляр координат жүйенің полюсі облыстың сыртқы нүктесі болса, онда A)

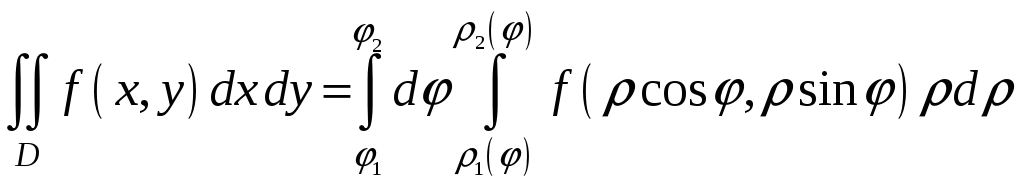
$$$ 93

Егер поляр координат жүйенің полюсі облыстың ішкі нүктесі болса, онда A)

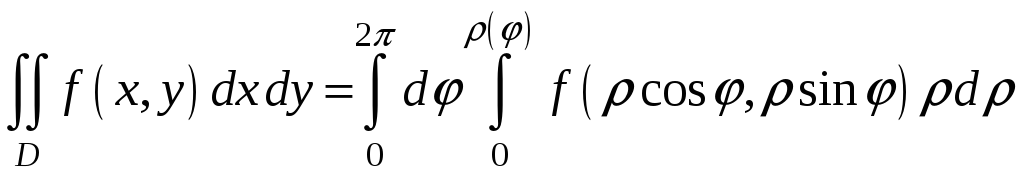
$$$ 94

Егер поляр координат жүйенің полюсі облыстың шекарасына тиісті болса , онда A)

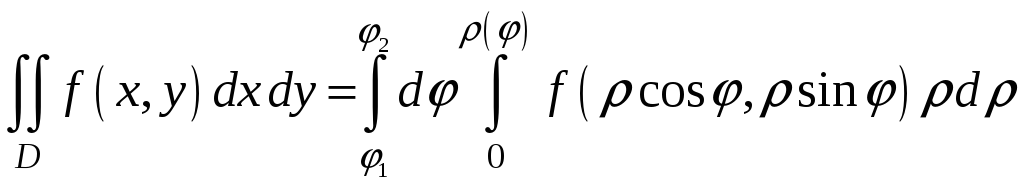
$$$ 95

Үш еселі интегралда декарт координат жүйеден цилиндрлік координат жүйеге көшу формуласы: A)

$$$ 96

Екі еселі интегралды есепте: 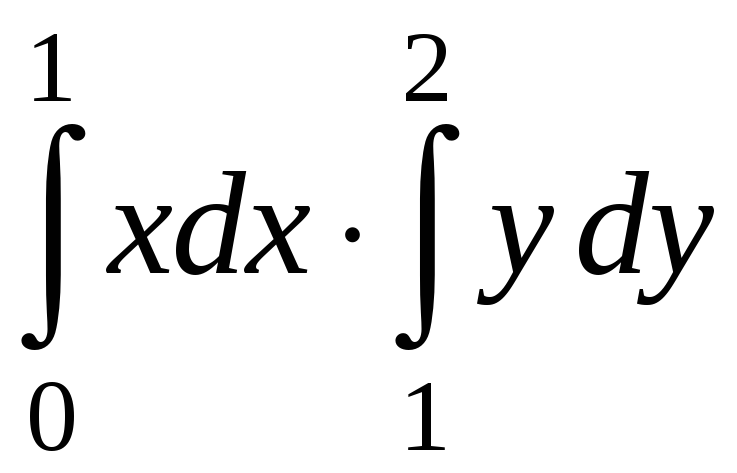A) 3/4

$$$ 97

Есепте: 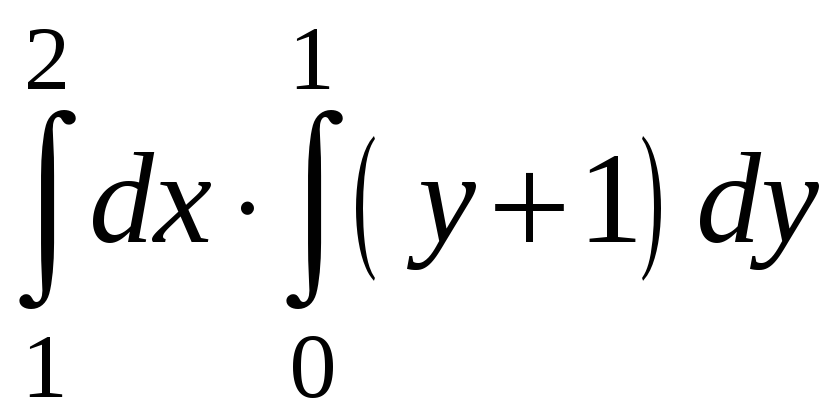A)

$$$ 98

Есепте: 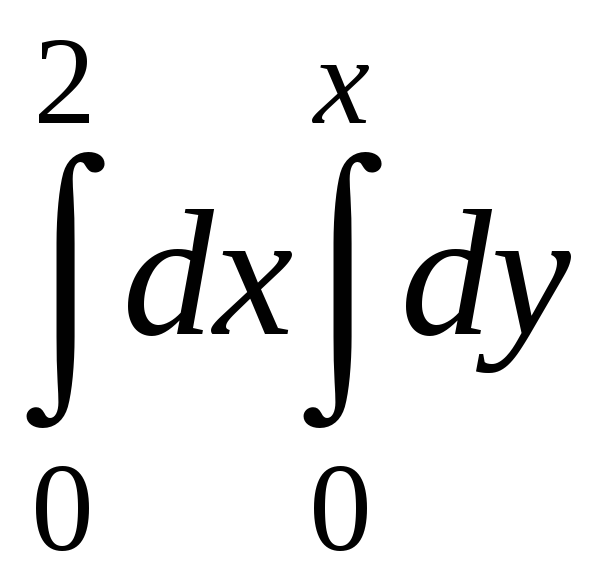A) 2

$$$ 99

Есепте: 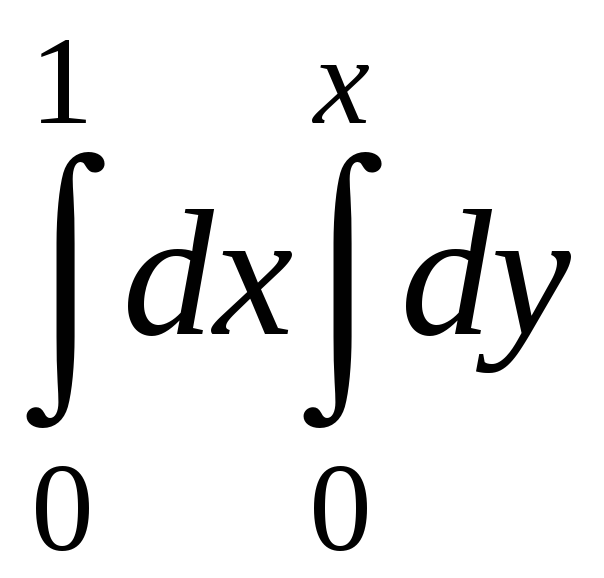A)

$$$ 100

Есепте: 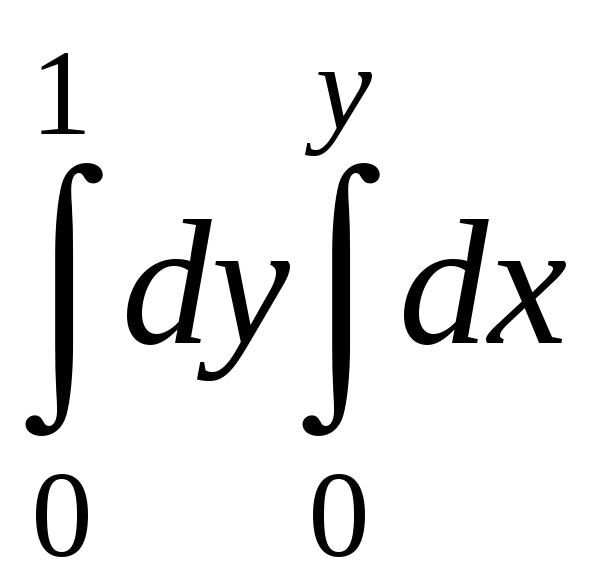A)

$$$ 101

Есепте: 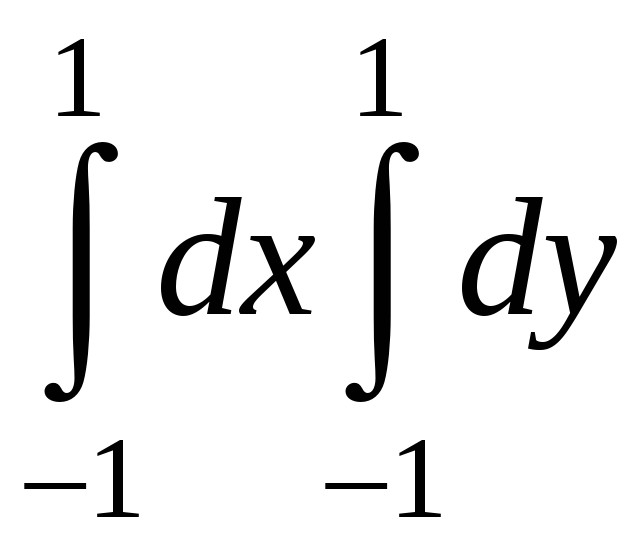A) 4

$$$ 102

Есепте: 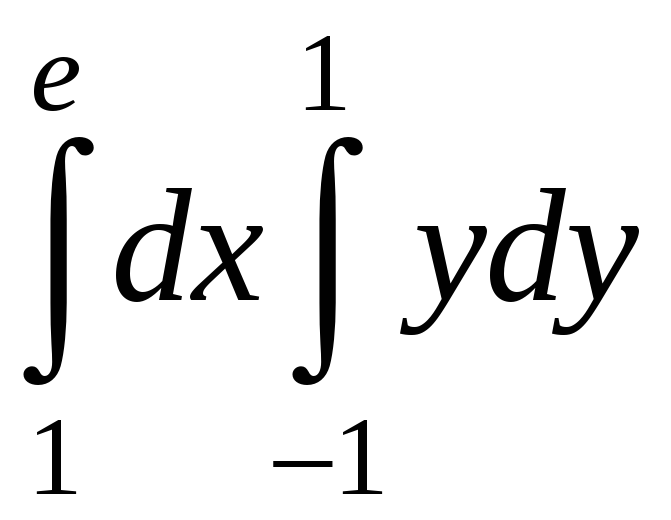A) 0

$$$ 103

Есепте: 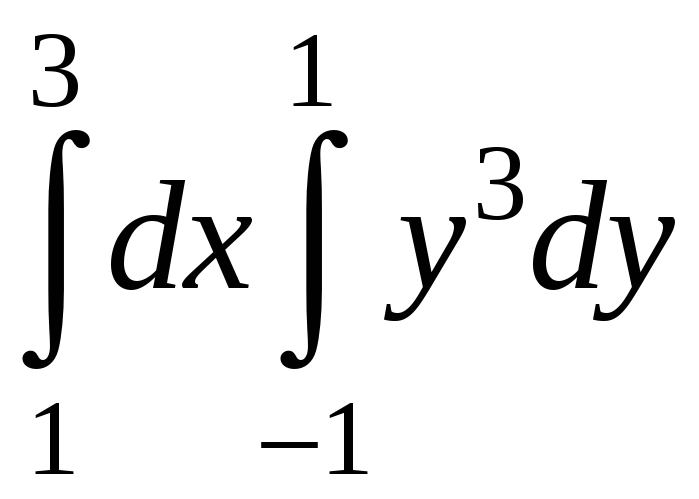A) 0

$$$ 104

Есепте: 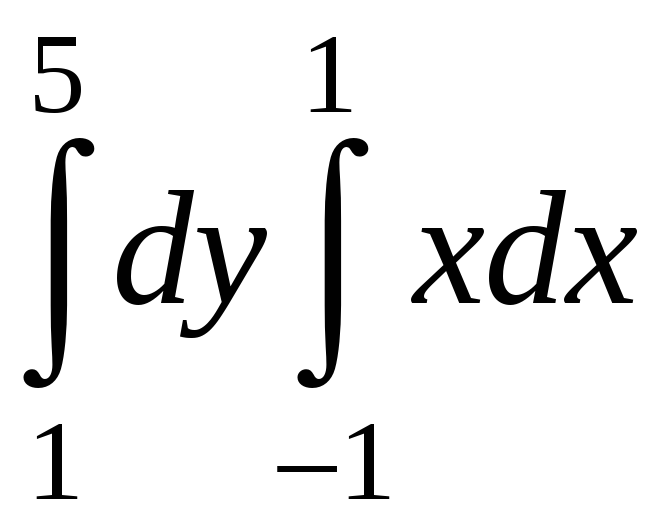A) 0

$$$ 105

Есепте: 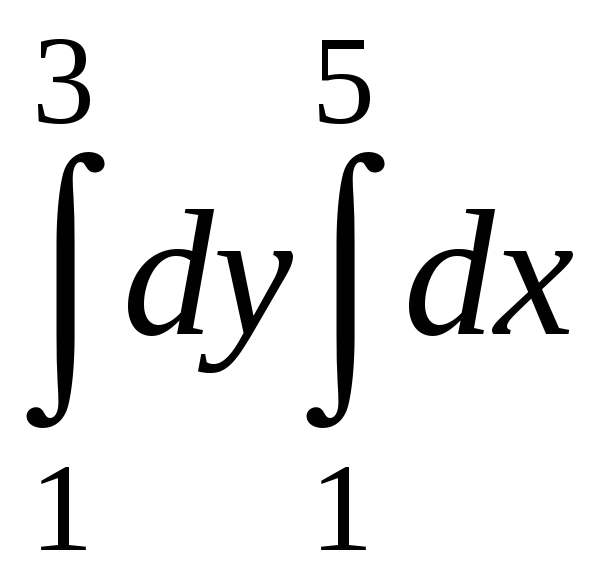A) 8

$$$ 106

Есепте: 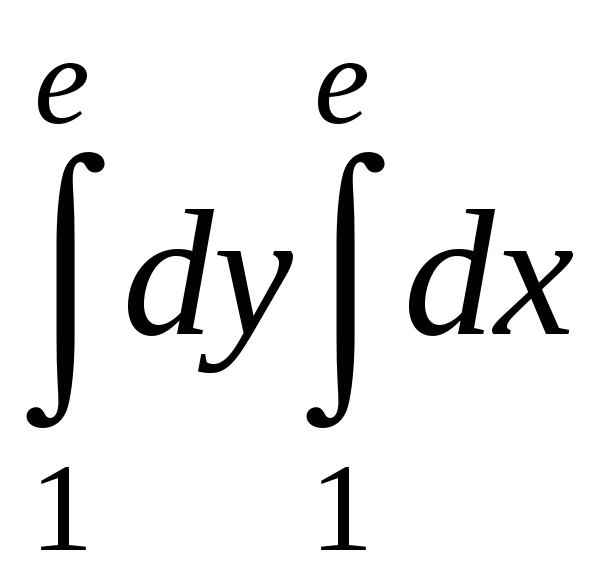A)

$$$ 107

Есепте: A) 0

$$$ 108

Егер интегралында алмастыруын жасасақ, онда көшу Якобианы неге тең?

А)

$$$ 109

Егер , мұндағы және аймақтарының шекаралары ортақ, онда

А)

$$$ 110

интегралы неге тең?

А) V аймағының көлеміне тең

$$$ 111

интегралы неге тең?

А) D аймағының ауданына

$$$ 112

полярлық координаталардан тіік бұрышты координаталарға көшу үшін қандай формула қолданылады?