Вычисление погрешностиТаранов

Вычисление погрешности

Как правило, вычисления производятся с числами, представленными в десятичном исчислении. Каждое число характеризуется числом значащих цифр или значностью. Например число 12,3 имеет три значащих цифры, как и число 1,23-10³, а число 0,024 две, а число 6,30 три( ноль в конце числа показывает, что здесь не единица или другая цифра, но конкретно ноль). Запятая в десятичном числе может быть умножением на порядок перенесена в любое место. Числа 1236,8 и 1,2368-10³ абсолютно равноценны. В практике принято две формы записи, например число 3 14,16 правильно (грамотно) можно представить в виде либо 3.141610², либо 0,31416-10³.

Любое число характеризуется своей абсолютной и относительной погрешностью. Если мы имеем число, то независимо от его природы оно характеризуется погрешностью окружения, которая равна половине последнего разряда. Число 1,236 имеет абсолютную погрешность ∆ = 0,0005 . Часто используется относительная погрешность δ как отношение абсолютной к самому числу и выраженная в процентах. Поэтому

∆ _1,236= 0,0005/1,236 = (0,05/1,236)%=0,040%

Относительная погрешность рассчитывается с точностью двух значащих цифр (больше бессмысленно, меньше грубо). Очень важно понять, что наложение запятой в числе не влияет на его погрешность. Погрешность чисел 12,36 и 0,1236 одинакова. В арифметических операциях могут участвовать несколько чисел, каждое из которых имеет свою погрешность. Результат вычислений с таким числом также будет иметь погрешность. Например, пусть а = 4,3 16 и b = 1,7 и необходимо вычислить

с = а/(b³) (1)

Непосредственное вычисление на калькуляторе дает с = 0,87848565. Но очевидно, что такая точность совершенно бессмысленна. Вопрос: сколько можно оставить значащих цифр в результате, чтобы с одной стороны не потерять точность, но и не писать то, что не гарантируется точностью исходных чисел? Из общей теории ошибок известно, что если имеется функциональная зависимость у от набора независимых х_i , которые заданы со своими погрешностями, то относительная погрешность δ (косвенная погрешность)

определяется по формуле

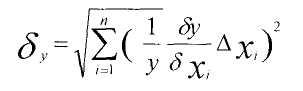(2)

где частные производные берутся его всеми х_i которые обладают абсолютными погрешностями ∆х_i . Арифметические операции удовлетворяют тем требованиям, при которых получена формула (2). Поэтому применяя (2) к выражению (1), получим

Но число (1,2*10^-2)² намного меньше числа у(2,9)² и поэтому δу ~ 8,7%. Таким образом в полученном числе С гарантируется результат, только с такой точностью, поэтому правильный результат должен быть записан в виде с = 0,88, т.е. только с двумя значащими цифрами. Из примера следует и более общий вывод: нельзя при вычислениях, имея на входе грубые числа, получить в результате вычислений результат с точностью большей, чем точность исходных чисел. Погрешность результата вычислений определяется погрешностью самого грубого числа, входящего в вычисления.