Глава 2. Исследование динамики кристаллической решетки наночастиц методом ядерного гамма резонанса
1.1 Модель Дебая твёрдого тела
Эффект Мёссбауэра связан с резонансным взаимодействием γ-кванта с ядром, при котором квантовое состояние решетки не меняется. Поэтому с помощью эффекта Мёссбауэра, казалось бы, нельзя получить информацию о движении атомов в решетке и о фононном спектре твердых тел. Однако имеется возможность изучения фононного спектра атомов в твердых телах посредством эффекта Мёссбауэра [38]. Она заключается в зависимости безфононной части γ-лучей от колебательных свойств твердых тел.
Действительно, для f-фактора Мёссбауэра-Лэмба имеем:
где 
–
средний квадрат амплитуды колебания
атома в направлении испускания γ-кванта,
усредненный по интервалу времени,
равному времени жизни уровня; λ – длина
волны γ-кванта.
Выражение (1) может быть записано в ином виде:
где
– энергия фотона. Для изотропного
кристалла;
Зависимость
безфононной части f
от спектра
колебания выражается, как видно из
формулы (1), через 
Чтобы выяснить зависимость f
от спектра
колебания, рассмотрим, как связано 
со спектром колебания
атомов в кристалле.
В теории физики
твердого тела кристалл представляется
как система 3Nосцилляторов
с частотой 
(N–число
атомов). Полная средняя энергия, связанная
с каждым осциллятором, равна
где – 
число
фононов на уровне 
Кинетическая
энергия кристалла, приходящаяся на j-й
осциллятор (в случае гармонического
осциллятора), 
равна половине полной энергии, т.е.
С другой стороны,
откуда
где 
– смещение атомов от j-го
осциллятора. Разделим обе части уравнения
на 
и
просуммируем по всем j:
Далее перейдем от суммирования к интегрированию, вводя плотность распределения частот ρ(ω):
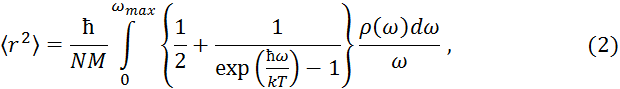
или
Из выражений (2) и
(3) следует зависимость 
от спектра колебания атомов в кристалле.
Величины 
и fзависят
от спектра колебания интегрально.
Поэтому, когда необходимо исследовать
зависимость fот
,
измеряют f
при различных
температурах, т.е. снимают кривую
зависимости 
и путем сравнения 
с теоретическими кривыми 
,
вычисленными при различных 
,
выбирают ту или иную модель кристалла.
В дебаевской модели твердого тела спектр частот колебания атомов имеет вид:
ρ(ω)=A
,
где А – нормировочных множитель, который находится из следующего условия:
Подставляя выражение (4) в (2), получим:
Введем температуру
Дебая
,
равную
и проведем частичное интегрирование:
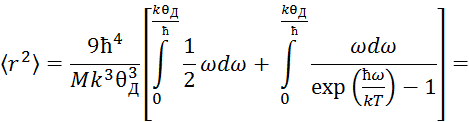
Обозначим 
После замены
переменных находим, что
Полученный в последнем выражении интеграл берётся численно и рассматривается как функция двух переменных:
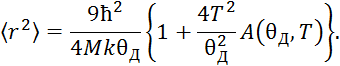
Подставим это выражение в формулу (1.1):
Поскольку в случае наноразмерных объектов температура Дебая может значительно отличатся от аналогичных макроскопических материалов, для данной формулы не может быть использовано ни каких приближений, в частности низко- и высокотемпературных. Поэтому выражение (6) должно использоваться в исходном виде как некая интегральная функция.
Таким образом, изучая температурную зависимость f-фактора можно определить температуру Дебая, которая является важным динамическим параметром любой кристаллической решетки. Однако существует множество других способов исследования динамики поверхности, рассмотрим подробнее два таких метода.