Основы программирования в среде Lazarus / Основы программирования в среде Lazarus / Основы программирования в среде Lazarus

Глава 6 Программирование приложений с графическим интерфейсом

____________________________________________________________________

begin Memo1.Clear;

n:=StrToInt(Edit1.Text); for h:=0 to n-1 do begin

x.Add('0');

end;

for k:=1 to n-1 do begin

for i:=k+1 to n do begin

if a.Strings[(k-1)*n+(k-1)]='0' then begin

{Начало блока перестановки уравнений}

p:=k; {В блок схеме используется буква l, но она похожа на цифру 1,

поэтому используем идентификатор p}

for r:=i to n do

if abs(StrToFloat(a.Strings[(r-1)*n+(k-1)]))> abs(StrToFloat (a.Strings[(p-1)*n+(k-1)])) then p:=r;

if p<>k then begin

for j:=k to n do; begin

t:=StrToFloat(a.Strings[(k-1)*n+(j-1)]); a.Strings[(k-1)*n+(j-1)]:= a.Strings[(p-1)*n+(j-1)]; a.Strings[(p-1)*n+(j-1)]:=FloatToStr(t);

end;

t:=(StrToFloat (b.Strings[k-1])); b.Strings[k-1]:=b.Strings[p-1]; b.Strings[p-1]:=FloatToStr (t);

end;

end; // Конец блока перестановок уравнений m:=StrToFloat (a.Strings[(i-1)*n+ (k-1)])/StrToFloat (a.Strings[(k-1)*n+(k-1)]); a.Strings[(i-1)*n+(k-1)]:='0';

for j:=k+1 to n do begin

a.Strings[(i-1)*n+(j-1)]:=

601

6.3 Визуальное программирование в среде Lazarus

____________________________________________________________________

FloatToStr(StrToFloat(a.Strings[(i-1) *n+(j-1)])-(m*StrToFloat(a.Strings[(k-1)* n+(j-1)])));

end; b.Strings[i-1]:=FloatToStr(StrToFloat (b.Strings[i-1])- (m*StrToFloat(b.Strings[k-1])));

end;

end;

{Проверка существования решения}

if StrToFloat (a.Strings[(n-1)*n+(n-1)])<>0 then {Решение существует и единственно}

begin x.Strings[n-1]:=(FloatToStr(StrToFloat

(b.Strings[n-1])/StrToFloat(a.Strings[(n-1)* n+(n-1)])));

for i:=n-1 downto 1 do begin

s:=0;

for j:=i+1 to n do begin

s:=s-StrToFloat (a.Strings[(i-1)*n+(j-1)])* StrToFloat (x.Strings[j-1]);

end; x.Strings[i-1]:=(FloatToStr((StrToFloat (b.Strings[i-1])+s)/

StrToFloat (a.Strings[(i-1)*n+(i-1)]))); end;

Memo1.Lines.Add('Решение:'); for j:=0 to x.Count-1 do

Memo1.Lines.Add('X'+IntToStr(j+1)+

'='+x.Strings[j]);

end else

if StrToFloat (b.Strings[n-1])=0 then Memo1.Lines.Add('Система уравнений'+

' не имеет решения.')

else

Memo1.Lines.Add('Система уравнений'+

' имеет бесконечное множество решений.');

end;

procedure TForm1.FormCreate(Sender: TObject); begin

602

Глава 6 Программирование приложений с графическим интерфейсом

____________________________________________________________________

A:=TStringList.Create;

b:=TStringList.Create;

x:=TStringList.Create;

v:=1;

v2:=1;

end;

procedure TForm1.Edit2Change(Sender: TObject); begin

if Edit2.Text = '-' then exit; StrToFloat (Edit2.Text); BitBtn1.Enabled:=true;

end;

procedure TForm1.BitBtn1Click(Sender: TObject); var n:integer;

begin

if (Edit2.Text= '-') or (Edit2.Text= '') then exit; begin

n:=StrToInt(Edit1.Text);

Edit2.SetFocus;

Edit2.SelectAll; if v2=1 then

Edit1.Enabled:=false; if v2<=n+1 then

begin

if v<=n+1 then v:=v+1

else v:=1;

if v<=n+1 then begin

if v<=n then Label3.Caption:='Введите a' +

IntToStr(v2) +

IntToStr(v);

if v>n then

Label3.Caption:='Введите b'+IntToStr(v2); A.Add(Edit2.Text);

end;

if v>n+1 then begin

b.Add(Edit2.Text);

603

6.3 Визуальное программирование в среде Lazarus

____________________________________________________________________

v2:=v2+1;

v:=1;

if v2<=n then Label3.Caption:='Введите a' +

IntToStr(v2)+

IntToStr(v)

else begin

Label3.Caption:='';

calculate;

BitBtn1.Enabled:=false;

Button1.SetFocus;

end;

end;

end; end else

Edit2.SetFocus;

end;

procedure TForm1.Button1Click(Sender: TObject); begin

b.Clear;

a.Clear;

x.Clear;

Memo1.Clear;

Edit1.Enabled:=true;

Edit1.Clear;

Edit2.Clear;

Edit1.SetFocus;

v:=1;

v2:=1;

Label3.Caption:='';

end;

procedure TForm1.Button2Click(Sender: TObject); begin

Close;

end;

procedure TForm1.Edit1Change(Sender: TObject); begin

if strtoint(Edit1.Text)>1 then begin

BitBtn1.Enabled:=true;

604

Глава 6 Программирование приложений с графическим интерфейсом

____________________________________________________________________

Edit2.Enabled:=true;

Edit2.Clear; Label3.Caption:='Введите a11'; Edit2.SetFocus;

end else begin

BitBtn1.Enabled:=false;

Edit2.Enabled:=false;

end;

end;

procedure TForm1.Edit1KeyPress(Sender: TObject; var Key: char);

begin

if Key = #13 then Key := #0; end;

initialization {$I Unit1.lrs}

end.

Проанализируем программу с двух точек зрения – с точки зрения пользо-

вателя и с точки зрения программиста.

С точки зрения пользователя мы видим, что программа может решать сис-

тему уравнений не более чем с девятью неизвестными. Попробуйте ввести дву-

значное число. У вас не получится!

Во-вторых, хотя ввод коэффициентов и организован более или менее удов-

летворительно, к сожалению, у пользователя нет возможности обозреть ранее введенные коэффициенты. При большом числе уравнений здесь немудрено до-

пустить ошибки, перепутать коэффициенты. Хотя подсказка, какой коэффици-

ент надо вводить в данный момент, присутствует.

Обратимся теперь к коду программы. В программе используется класс

TStringList. Но, вообще говоря, класс TStringList не предназначен для вычислений! Он предназначен для обработки строк, т.е. для обработки сим-

вольной информации. Посмотрите сколько здесь производится преобразований

605

6.3 Визуальное программирование в среде Lazarus

____________________________________________________________________

из символьного представления в числовое и обратно.

В программах такого рода, где в основном производятся вычисления,

обычно преобразования выполняются всего два раза! В начале работы про-

граммы (при вводе исходных данных) строки символов преобразуются в числа,

производятся все необходимые вычисления и в конце работы программы полу-

ченные результаты (числовые) преобразуются в их строковое представление для вывода на экран или принтер. При всех прочих равных условиях, эта про-

грамма будет работать на порядок (если не больше) медленнее, чем программа,

в которой сначала все данные преобразованы в числа.

Теперь посмотрите на код, которым реализован ввод коэффициентов. Там

"сам черт ногу сломит"! Используется слишком много условных операторов.

Кроме того, в программе напрочь отсутствует контроль вводимых данных.

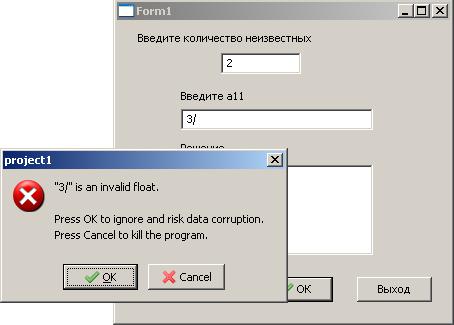
Хотя стандартная реакция системы поможет избежать аварийного завершения программы, рис. 6.58.

Рис. 6.58. Пример возникновения исключения

Нажав кнопку ОК, пользователь еще может ввести правильное число.

Давайте исправим программу с учетом сделанных выше замечаний. Чтобы

606

Глава 6 Программирование приложений с графическим интерфейсом

____________________________________________________________________

пользователь мог видеть все введенные коэффициенты, а также редактировать их удобнее применить компонент TStringGrid. Поэтому, сначала познако-

мимся с этим компонентом.

6.3.10.2. Компонент TStringGrid

TStringGrid находится во вкладке Additional и имеет вид, рис. 6.59.

Рис. 6.59. Вид компонента TStringGrid

Компонент представляет собой таблицу, состоящую из строк Rows и

столбцов Cols. В свою очередь таблица это двумерный массив, значениями которого являются строки символов и, следовательно, имеет тип string. Дос-

туп к данным осуществляется через свойство Cells. Ячейке таблицы, нахо-

дящейся на пересечении столбца с номером Col и строки с номером Row, соот-

ветствует элемент массива Cells[Col,Row]. Обратите внимание, вначале указывается столбец, а затем строка. Нумерация столбцов и строк начинается с нуля. Основные свойства компонента TStringGrid следующие:

ColCount – количество столбцов таблицы;

RowCount – количество строк таблицы;

FixedCols – количество фиксированных столбцов таблицы. Обычно фик-

сируется один, самый левый столбец и используется для задания постоянной информации, например, заголовка столбца. Но можно зафиксировать и больше

607

6.3 Визуальное программирование в среде Lazarus

____________________________________________________________________

столбцов. При этом зафиксированные столбцы выделяются цветом и при гори-

зонтальной прокрутке таблицы остаются на месте;

FixedRows – количество фиксированных строк таблицы. Точно так же,

фиксируется обычно одна строка для задания заголовка, но можно зафиксиро-

вать и больше строк. Строки выделяются цветом и при вертикальной прокрутке таблицы остаются на месте;

FixedColor – цвет фиксированных строк и столбцов.

VisibleColCount – количество видимых (прокручиваемых) столбцов,

равно ColCount – FixedCols;

VisibleRowCount – количество видимых (прокручиваемых) строк, равно

RowCount – FixedRows;

ScrollBars – определяет наличие в таблице полос прокрутки. Если ука-

зать значение ssAutoBoth, то полосы прокрутки будут появляться и исчезать автоматически в зависимости от того, помещается таблица в окно компонента или нет.

Во вкладке Options свойств TStringGrid определены ряд свойств,

наиболее важными из которых являются:

goEditing – разрешает или запрещает редактирование содержимого яче-

ек таблицы. true – редактирование разрешено, false – запрещено;

goTab – разрешает (true) или запрещает (false) использование клави-

ши <Таb> для перемещения курсора в следующую ячейку таблицы;

goAlwaysShowEditor – признак нахождения компонента в режиме ре-

дактирования. Если значение свойства false, то для того, чтобы в ячейке поя-

вился курсор, надо начать набирать текст, нажать клавишу <F2> или сделать щелчок мышью.

Итак, вернемся к реализации метода Гаусса решения системы линейных алгебраических уравнений. Для ввода коэффициентов расширенной матрицы системы воспользуемся компонентом TStringGrid. Создайте новый проект и

608

Глава 6 Программирование приложений с графическим интерфейсом

____________________________________________________________________

спроектируйте вид приложения так, как показано на рисунке 6.60.

Установите следующие свойства компонента TStringGrid:

ColCount = 1; RowCount = 1; FixedCols = 0; FixedRows = 0;

goEditing = true; goTab = true;

goAlwaysShowEditor = true;

Рис. 6.60. Форма приложения

Код программы:

unit Unit1;

{$mode objfpc}{$H+} interface

uses

Classes, SysUtils, LResources, Forms, Controls, Graphics, Dialogs, StdCtrls, Buttons, Grids, LCLType, LCLProc;

type

{ TForm1 }

TForm1 = class(TForm) Button1: TButton; Button2: TButton; Button3: TButton; Button4: TButton; Button5: TButton; Edit1: TEdit;

609

6.3 Визуальное программирование в среде Lazarus

____________________________________________________________________

Label1: TLabel;

Label2: TLabel;

Label4: TLabel;

Memo1: TMemo; StringGrid1: TStringGrid;

procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject); procedure Button4Click(Sender: TObject); procedure Button5Click(Sender: TObject); procedure Edit1KeyPress(Sender: TObject;

var Key: char); procedure FormShow(Sender: TObject); procedure Gauss(var vector: array of extended;

var b: array of extended; var x: array of extended; var n: integer);

procedure StringGrid1KeyDown(Sender: TObject; var Key: Word;

Shift: TShiftState); private

{private declarations } public

{public declarations } end;

var

Form1: TForm1; n: integer;

a:array of array of extended;{матрица коэффициентов системы, двумерный динамический массив}

vector: array of extended; {преобразованный одномерный динамический массив }

b:array of extended;

x: array of extended; implementation

{ TForm1 }

procedure TForm1.Gauss(var vector: array of extended; var b: array of extended; var x: array of extended; var n: integer);

var

a: array of array of extended;{матрица коэффициентов системы, двумерный динамический массив}

i, j, k, p, r: integer;

610