Практикум по программированию Обработка числовых данных

program Project2; {$APPTYPE CONSOLE} uses

SysUtils; type

tn=array[-1..1] of Integer; tmn2=array[1..2] of tn; tmn4=array[-5..-2] of tn;

procedure Pp1(mn:array of tn; out s:Integer); var i,j:Integer;

begin s:=0;

for i:=Low(mn) to High(mn) do for j:=Low(tn) to High(tn) do

//или для второго измерения статического массива

//for j:=Low(mn[0]) to High(mn[0]) do begin

s:=s+mn[i,j];

WriteLn(' i=',i,' j=',j:2

,' mn[i,j]=',mn[i,j],' s=',s);

end;

end;

var A:tmn2=((5,3,7),

(7,9,2));

B:tmn4=((2,4,1),

(7,6,2),

(0,1,8),

(3,7,5));

r:Integer;

begin // РАЗДЕЛ ОПЕРАТОРОВ ПРОГРАММЫ WriteLn('Вызов процедуры '

,'для обработки матрицы A'); Pp1(A,R);

WriteLn('Сумма элементов массива B = ',R); WriteLn;

WriteLn('Вызов процедуры '

,'для обработки матрицы B'); Pp1(B,R);

WriteLn('Сумма элементов массива B = ',R); ReadLn;

end.

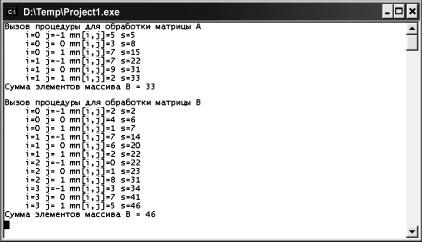
Результат работы программы представлен на рис. 6.7.

Ðèñ. 6.7

Следует обратить внимание на граничные значения индексо в, представляющих номера строк и столбцов. Номера строк изме няются от 0 до значения, на единицу меньшего числа строк в фак - тическом массиве, так как формальный параметр является от крытым массивом (по количеству содержащихся в нем одномерны х массивов типа tn), а номера столбцов изменяются от −1, как в массивах — фактических параметрах, до 1 , так как для типа статического массива стандартные функции Low и High возвращают минимальное и максимальное значения индексов из объяв ления типа статического массива.

Динамические массивы

Наиболее удобным способом рационального использования оперативной памяти для хранения массивов данных, размеры кот о- рых не определены или могут меняться в широком диапазоне, является применение динамических массивов. При объявлен ии таких массивов не указывают границы индексов. Объявив тип

tmas=array of Real;

можно использовать его для объявления динамических масс ивов, например,

var A,B,C:tmas;

размеры которых можно задавать и изменять динамически (п о мере необходимости) с помощью стандартной процедуры SetLength. Например, при выполнении SetLength(A,3) размер массива A станет равным 3. В дальнейшем с помощью процедуры SetLength можно увеличить или уменьшить размер массива. В динамических массивах для индексации используют только це лые значения, минимальное значение индекса всегда 0. Минимальное значение индекса массива определяется стандартной функ цией Low (всегда 0), максимальное значение индекса — стандартной функцией High, а длина (размер) — стандартной функцией Length (как для открытых массивов в подпрограммах). При увеличени и размера прежние элементы сохраняют свои значения, а новые со значениями 0 добавляются в конец массива. При уменьшении р азмера пропадают элементы с наибольшими индексами, а осталь - ные сохраняют свои значения. При задании нуля в качестве р азмера массива занимаемая им память освобождается полност ью.

Объявив двумерные динамические массивы, например, type tmatr=array of array of Real;

в подпрограмму можно передавать матрицу (двумерный масси в) с произвольным количеством строк и столбцов. В общем случ ае динамический массив с любым числом измерений и размерами может использоваться в качестве фактического параметра , соответствующего формальному параметру «открытый массив», п ри- чем в теле подпрограммы для любого его измерения можно бу - дет найти длину и максимальное значение индекса (минимал ь- ное всегда равно 0), используя имя формального параметра и стандартные функции Length и High (для статических массивов при числе измерений, больше 2, для определения в подпрограм - ме диапазонов младших индексов потребуется использоват ь имена типов, что снижает универсальность подпрограммы). Наприм ер, для вычисления суммы элементов трехмерного динамическо го массива X, имеющего тип tkmn:

type

tmn=array of array of Integer; tkmn=array of tmn;

подпрограмму можно оформить так:

procedure Sum1(const a:array of tmn; out r:Integer);

var i,j,k:integer; begin

r:=0;

for k:=Low(a) to High(a) do

for i:=Low(a[0]) to High(a[0]) do for j:=Low(a[0,0]) to High(a[0,0]) do

r:=r+a[k,i,j];

end;

Выделение памяти и указание пределов изменения индексов по каждому измерению динамического массива производитс я в процессе выполнения программы процедурой SetLength(a,n).

Нижняя граница индексов по любому измерению динамическо - го массива всегда равна нулю. Наибольший индекс примет то гда значение n − 1, где n — количество элементов массива, задаваемое при обращении к процедуре SetLength, а первый параметр — имя массива. При выделении памяти под матрицу можно выпол - нить обращение SetLength(b,m,n), если матрица имеет прямоугольную форму, т. е. количество элементов во всех строках о динаково и равно n (m — количество строк матрицы).

Использование динамических массивов позволяет работать с матрицами, у которых в каждой строке разное количество эл е- ментов. При выделении памяти для многомерных массивов (в частности, для хранения двумерных матриц) сначала устана вливается длина первого измерения, затем второго, третьего и т. д. Например, выделим память для хранения элементов треуголь ной матрицы:

. . . . .

var

a:array of array of Real; n,l,j:Integer;

begin // РАЗДЕЛ ОПЕРАТОРОВ ПРОГРАММЫ ReadLn(n);

SetLength(a,n); for i:=0 to n-1 do

Setlength(a[i],i+1);

. . . . .

end.

При изменении длины уже созданного динамического массива сначала резервируется память для размещения нового мас-

сива, затем элементы старого копируются в новый, после чег о освобождается память, выделенная под первоначальный мас сив.

Для освобождения памяти помимо процедуры SetLength можно использовать процедуру Finalize или идентификатору массива присвоить значение nil. Например, для освобождения памяти в предыдущем примере можно записать оператор a:=nil или

Finalize(a).

Перегружаемые подпрограммы

В рамках одной программы можно объявить несколько подпрограмм (процедур или функций) с одинаковыми именами, но различающихся по типу или числу параметров. Если при объя в- лении заголовка подпрограммы поставить ключевое слово overload, то компилятор после анализа фактических параметров в выз ове подпрограммы выберет подходящий вариант из числа одноим енных подпрограмм. Например, при делении целых чисел их надо делить нацело, а при делении действительных чисел требует ся получать результат действительного типа. В этом случае сл едует объявить две одноименных функции деления, у которых будет различный тип аргументов, а также различаться тип результ ата:

program Funperegr; {$APPTYPE CONSOLE} uses

SysUtils; var

a,b,c:Real;

k,l,m:Integer;

function Divide(a,b:Real):Real; overload; begin

Result:=a/b;

end;

function Divide(a,b:Integer):Integer; overload; begin

Result:=a div b; end;

begin // РАЗДЕЛ ОПЕРАТОРОВ ПРОГРАММЫ ReadLn(a,b);

c:= Divide(a,b);

ReadLn(k,n);

m:= Divide(k,l);

WriteLn('c =',c:6:2,' m=',m); ReadLn;

end.

При вводе a = 3 è b = 2 будет вызвана функция, выполняющая деление вещественных чисел, так как a и b — вещественные переменные, и выведено c = 1.5. При вводе k = 3 è n = 2 будет вызвана функция, выполняющая деление целых чисел, так как k и n — переменные целого типа, и будет выведено m = 1.

Параметры со значениями по умолчанию

Параметры в объявлении подпрограмм можно задавать по умолчанию. Значение по умолчанию — это значение, использу е- мое при вызове подпрограммы, если в нее не передано факти- ческое. Использование параметров по умолчанию равносиль но разрешению указывать в вызове подпрограммы не все необхо - димые параметры.

Значения по умолчанию задают добавлением после объявления типа формального параметра знака равенства, после кот орого записывается константное выражение. Рассмотрим функц ию, которая рассчитывает силу тяжести бруска в форме прямоуг ольного параллелепипеда в зависимости от его размеров, матер иала (плотности) и ускорения свободного падения:

program Funumpar; {$APPTYPE CONSOLE} uses

SysUtils; var

a,b,c,ro,g:Real;

p1,p2,p3,p4:Real;

function St(a:Real=4; b:Real=5; c:Real=6; ro:Real=7.8; g:Real=9.81):Real;

begin st:=a*b*c*ro*g;

end;

begin // РАЗДЕЛ ОПЕРАТОРОВ ПРОГРАММЫ ReadLn(a,b,c,ro,g);

p1:=St(a,b,c,ro,g); p2:=St(); //èëè p2:=st; p3:=St(a,b,c,ro); p4:=St(a,b,c);

WriteLn('p1=',p1:7:2,' p2=',p2:7:2 ,' p3=',p3:7:2,' p4=',p4:7:2);

ReadLn;

end.

При первом обращении к функции вычисляется сила тяжести бруска при значениях всех параметров, введенных в осно вной программе с клавиатуры, во втором случае, наоборот, все пар а- метры берутся по умолчанию, т. е. вычисления ведутся с теми значениями, которые заданы в заголовке функции. В третьем слу- чае по умолчанию берется только ускорение свободного пад е- ния, а в четвертом случае — плотность вещества и ускорение свободного падения.

Аргументы по умолчанию должны быть самыми правыми (последними) в списке параметров подпрограммы, при передаче п а- раметров действует правило: если пропущенный параметр не является последним, то и все параметры, стоящие справа от нег о, тоже пропускаются. Принимая это правило во внимание, след ует сделать вывод о том, что последними в списке параметров по умолчанию надо указывать те, которые чаще всего остаются равными заданным по умолчанию значениям. Пропускать при вызо - ве можно только несколько последних параметров по умолча нию. Нельзя вызвать функцию следующим образом: p1:=St(a,,c,ro,g). Значения по умолчанию могут задаваться не всем, а только н е- которым параметрам подпрограммы. При этом они должны располагаться в конце списка параметров, так как действует п равило: если какой-то параметр имеет значение по умолчанию, то и все последующие должны иметь значения по умолчанию.

Примеры организации программ с подпрограммами

Пример 1. Определить в матрице все элементы, которые являются числами Фибоначчи, и переписать их в одномерный массив. Полученный массив упорядочить по возрастанию.

Числа Фибоначчи образуются по следующему правилу: f0 = 1,

f1 = 1, fi = fi−2 + fi−1 (i ³ 2).

Программирование проведем с использованием подпрограмм . Составим функцию, которая определяет, является ли число, п ереданное в качестве аргумента, числом Фибоначчи. Кроме того , со-

ставим процедуру упорядочения элементов одномерного ма ссива по возрастанию. Для проверки правильности выполнения отд ельных этапов алгоритма выведем получаемый массив чисел Фиб о- наччи до его упорядочения и после. В этом случае целесообр азно составить процедуру вывода элементов одномерного масси ва, так как это действие приходится осуществлять дважды. Для прид ания программе большей универсальности будем использовать д инами- ческие массивы.

Проверку заданного числа на число Фибоначчи будем проводить путем его последовательного сравнения со всеми чи слами Фибоначчи, начиная с единицы. Процесс сравнения заканч и- вается, если заданное число оказалось числом Фибоначчи ил и очередное число Фибоначчи превысило заданное число.

Для упорядочения чисел используется алгоритм пузырьков ой сортировки:

program Procfib; {$APPTYPE CONSOLE} uses

SysUtils; type

matr=array of array of Integer; mas=array of Integer;

var

a:matr; b:mas; m,n,i,j,k:Integer;

//Функция, определяющая, является ли //заданное число числом Фибоначчи function Fib(a:Integer):Boolean; var

f0,f1,f2:Integer; begin

Result:=False;

f1:=0;f2:=1; repeat

f0:=f1;

f1:=f2;

f2:=f0+f1;

if a=f2 then Result:=True until Result or(f2>=a);

end; //конец функции Fib

//Процедура упорядочения элементов //одномерного массива по возрастанию procedure Upor(var b:mas);

var i,k,c,n:Integer; pr:boolean;

begin n:=High(b); k:=0; repeat

k:=k+1;

pr:=True;

for i:=0 to n-k do if b[i]>b[i+1] then begin

c:=b[i];

b[i]:=b[i+1];

b[i+1]:=c;

pr:=False;

end; until pr;

end; //конец процедуры Upor

//Процедура вывода элементов одномерного массива procedure Wiwod(const b:mas);

var i:Integer;

begin

for i:=0 to High(b) do Write(b[i]:4); WriteLn;

end; //конец процедуры Wiwod

begin //РАЗДЕЛ ОПЕРАТОРОВ

WriteLn('Введите количество строк и столбцов'); ReadLn(m,n);

SetLength(a,m,n);

Writeln('Введите матрицу по строкам'); for i:=0 to m-1 do

begin

for j:=0 to n-1 do Read(a[i,j]);

ReadLn;

end;

WriteLn('Исходная матрица'); for i:=0 to m-1 do

begin

for j:=0 to n-1 do Write(a[i,j]:4); WriteLn;

end;

k:=0;

for i:=0 to m-1 do for j:=0 to n-1 do

if Fib(a[i,j]) then begin

k:=k+1;

SetLength(b,k); b[k-1]:=a[i,j];

end; if k=0 then

WriteLn('В матрице нет чисел Фибоначчи') else

begin

WriteLn('Массив чисел Фибоначчи'); Wiwod(b);

Upor(b);

WriteLn('Упорядоченный массив ' ,'чисел Фибоначчи');

Wiwod(b);

end;

ReadLn;

end.

Пример 2. Определить в каждой строке матрицы A(m, n), m ≤ 10, n ≤ 12 первое по порядку простое число и занести его в одномерный массив. Если в строке нет простых чисел, то для этой строки занести в массив нулевой элемент.

Поскольку максимальные размеры матрицы заданы в условии, в программе целесообразно использовать статические массивы. Определение вида числа (простое или нет) проведем в подпрограмме-функции, которая возвращает значение истина, если число простое, и ложь — в противном случае.

Для определения вида числа следует определить остатки от деления этого числа на все целые, начиная с двух и заканчив ая