Оптимальный фильтр.

ОФ обеспечивают на выходе максимальное отношение мощности обнаруживаемого сигнала к средней мощности шума или помехи. Каким должен быть частотный коэффициент передачи такого фильтра?

Входной сигнал: ,- частотная характеристика.

Для мощности сигнала на выходе оптимального фильтра в момент его окончания t₀имеем (выходное сопротивление 1 Ом):.

Для мощности шума: - средняя мощность шума на выходе,- спектральная плотность мощности белого шума ().W₀в расчете на положительные «».

Тогда для отношения мощностей сигала и шума получим: (*).

Каким должно быть , чтобы получить максимум выражения (*)?

Воспользуемся неравенством Коши-Буниковского-Шварца: . Причем знак равенства достигается при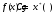, причем С – произвольная константа.

Перепишем его в виде .

Сопоставим левую часть неравенства с правой частью уравнения (*). Они совпадают, если переобозначить . Отсюда следует, что максимальное значение уравнения (*) достигается при(**). И в этом случае максимум.

В числителе последнего отношения, согласно равенству Парсеваля, стоит полная энергия сигнала. Поэтому, можно написать 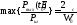(***) - теоретический максимум отношения сигнал/шум.

Таким образом, из наиболее общего требования, предъявляемого к оптимальному фильтру, было выведено выражение для частотного коэффициента передачи (**) и теоретический предел отношения сигнал/шум.

Оптимальный фильтр: , гдеt­₀ – момент окончания входного сигнала,.

Отметим следующие особенности коэффициента передачи:

1. Особенности частотной зависимости .

Рис.15.

Вывод:частотный коэффициент оптимального фильтра «привязан» рациональным способом к спектру входного сигнала – он отличен от нуля там, где есть сигнал, и равен нулю там, где кроме шума нет ничего.

2. Посчитаем :

Таким образом, выходной оптимальный сигнал формируется синфазным сложением всех гармонических составляющих входного сигнала.

3. Как измениться частотный коэффициент оптимального фильтра, если входной сигнал сдвинуть во времени?

Рис.16.

Сигналы идентичны, и отличаются лишь моментом окончания на входе оптимального фильтра. Посчитаем Фурье компоненты смещенного сигнала.

Соответственно, для частотного коэффициента передачи оптимального фильтра смещенного сигнала получим: . Следовательно, максимум отношения сигнал/шум () будет реализован в оптимальном фильтре для данного вида сигнала не зависимо от момента его прихода на ОФ.

4. Импульсная характеристика оптимального фильтра.

Импульсная характеристика – это отклик устройства на короткий входной импульс, в переделе на импульс в виде дельта функции (,).

Спектр дельта функции будет: .

Импульсная характеристика: .

Импульсная характеристика связана с частотным коэффициентом передачи преобразованием Фурье. Очевидны и обратные преобразования.

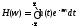
То есть зная одну из характеристик всегда можно рассчитать другую. Это и означает, что импульсная характеристика характеризует устройство так же полно, как и частотный коэффициент.

Расчет импульсной характеристики оптимального фильтра.

Рис.17.

Реализация оптимальных фильтров.

Оптимальный фильтр для прямоугольного видеоимпульса.

Рис. 18.

Ищем спектр: .

Построим структурную схему оптимального фильтра сопоставляя каждой части формулы какое-то передаточное звено.

Рис.19.

Структурная схема является по сути графическим изображением формулы.

Докажем, что передаточные функции интегратора и линии задержки такие, как указаны на рисунке. Связь входного и выходного сигналов передаточной функции вида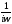определяется формулой:

Линия задержки: .

Выходной сигнал повторяет входной сигнал только с задержкой на .

Оптимальный фильтр для прямоугольного радиоимпульса.

Рис.20.

Для простоты рассуждений будем предполагать, что в пределах радиоимпульса расположено целое число полуволн ВЧ заполнения.

В данном случае, импульсная характеристика совпадает с самим радиоимпульсом.

Структурная схема, имеющая импульсную характеристику данного вида будет.

Рис.21.

Оптимальный фильтр для пачки одинаковых импульсов.

Импульсы могут быть как видео- так и радиоимпульсами.

Рис.22.

Чтобы построить воспользуемся структурной схемой получения пачки импульсов из одного импульса (вместо громоздкой линии преобразования).

Рис.23.

Воспользовавшись передаточной функции линии задержки можем написать формулу для компонента спектра пачки импульсов:

Воспользуемся формулой для частотного коэффициента оптимального фильтра, полагая в ней .

На основе данной формулы построим структурную схему.

Другое воплощение формулы приводит к схеме рециркулятора, преимущество которого заключается в том, что в нем нет многоотводной линии задержки, а всего лишь одна линия задержки.

Усилитель компенсирует потери в ЛЗ, а петля ОС накапливает импульсы по мере их поступления.