Нпио. Вводная лекция.

Нанотехнология– совокупность способов создания элементов и приборов из отдельных атомов и молекул (1 – 100 нм).

Нанотехнологии в электронике.

МОП транзисторы с длинной канала ~ 0,1 мкм.

Рис.1.

При переходе к размерам 0,05 мкм появились новые эффекты, которые делали нерабочими транзисторы традиционной конструкции. В этом случае, стали значительно проявляться волновые свойства электрона. Они стали доминирующими над корпускулярными.

Волновая природа электрона.

Волновое представление ввел де Бройль в 1924 г. В любой частице с импульсом Pсоответствует волна с длинной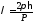, где- редуцированная постоянная Планка.

Оценим длину волны де Бройля в вакууме, металле и полупроводнике.

Рис.2.

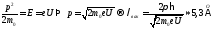, гдеm₀– масса электрона в вакууме (9,1*10^-31кг), е – заряд электрона (1,6*10^-19Кл).

Металл.

Рис.3.

Полупроводник.

Рис.4.

Это существенно меньше, чем энергия Фермиевских электронов в металле. Эффективная масса электрона в полупроводнике существенно меньше, чем в металле.

Для оценки возьмем

Квантовая механика как основа описания нано-объектов.

	Микроэлектроника	Наноэлектроника
Электрон	Частица	Волна
Ток	Поток частиц	Перераспределение волновой функции

Электрон – как частица по второму з-ну Ньютона .

Электрон – как волна де Бройля: временное уравнение Шредингера ,

где – волновая функция,- оператор Гамильтона,- потенциальная энергия.

Для стационарного состояния: или(стационарное уравнение Шредингера).

Физический смысл волновой функции: - определяет плотность вероятности нахождения электрона в точке, с координатами.- полная вероятность обнаружения электрона в объеме.

Рассмотрим в качестве примера расчет волновой функции электрона, находящегося в нанослое.

Рис.5.

Наноразмерный - Lz.

Ищем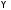в виде. при подстановке в уравнение Шредингера преобразуем к виду:.

Сделаем еще одно упрощение. Будем считать, что потенциальная яма, ограничивающая положение электрона вдоль z, является бесконечно глубокой (модель БПЯ).

Ри.6.

Внутри ямы будем искать волновую функцию в виде ,,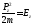 гдеAиB– константы, которые находятся из граничного условия:(следствие бесконечности размера ямы).

(*)

Решение существует, если det* = 0, следовательно,(по формуле Эйлера)., следовательно,.

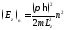Таким образом, полная энергия электрона в слое .

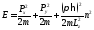Первые два слагаемых принимают непрерывный ряд значений начиная с 0. Последнее слагаемое дискретно и имеет не нулевое минимальное значение, так что ,

Не нулевое значение энергии электрона в наноразмерном объекте и дискретность энергетических состояний, возникающих как следствие волнового поведения электрона в замкнутом пространстве называется эффектом квантового ограничения (quantum confinement).

Система уравнений для AиBпозволяет найти их с точностью до множителя. Чтобы найти абсолютные значенийAиBнужно наложить на волновую функцию еще одно условие, помимо граничных условий – условие нормировки, выражающее единичную вероятность (100%) нахождения электрона, где-либо вдоль всей осиZ:.

С этим дополнительным уравнением можно найти абсолютные значения AиB, и соответствующую им волновую функцию.

Выполнив все расчеты, получим волновые функции 2-х типов: , гдеn– нечетные;,n– четные.

Рис.7.