
2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy
.pdf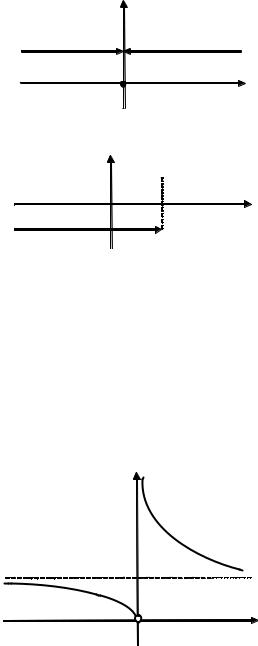
y
1 |
y = (signx)2 |
|
О |
x |
Рис. 2.7. В точке х = 0 функция имеет устранимый разрыв
y
1 

О |
2 |
x |
|
– 1
Рис. 2.8. В точке х = 2 функция имеет разрыв первого рода. f(2 + 0) – f(2 – 0) = 2
Например: функция |
f (x) = |
x − 2 |
(рис. 2.8) не определена в точке |
|
|||
|
|
x − 2 |
|
х = 2, но lim f (x) = −1, |
lim f (x) =1. |
||
x→2−0 |
x→2+0 |
|
|
Если в точке а не существует хотя бы один из односторонних пределов, то это точка разрыва второго рода.
Например: функция f(x) = е1/х (рис. 2.9) не определена в точке х = 0 и
lim f (x) = +∞ , |
lim f (x) = 0 . |
x→+0 |
x→−0 |
y |
у = е1/х |
|
|
1 |
|
О |
x |
Рис. 2.9. В точке х = 0 функция имеет разрыв второго рода
61
2.11. Свойства функций, непрерывных в точке
Свойство 1. Если функция непрерывна в точке а, то существует такая окрестность этой точки, в которой функция ограничена, т.е.
δ > 0 С > 0 : x Uδ (a) → | f (x) | < C .
Свойство 2. Если функция непрерывна в точке а и отлична от нуля, то существует такая окрестность этой точки, в которой функция сохраняет знак числа f(a), т.е.
δ > 0 : x Uδ (a) → signf (x) = signf (a) .
Свойство 3. Если функции f(x) и сумма, произведение и частное (если
g(x) непрерывны в точке а, то их g(а) ≠ 0) непрерывны в этой точке.
Свойство 4. Если функция z = f(y) непрерывна в точке y0, а функция y = ϕ(x) непрерывна в точке х0, причем y0 = ϕ(x0), то в некоторой окрестности точки х0 определена сложная функция f(ϕ(x)), непрерывная в точке х0.
Доказательство. Свойства 1 – 3 являются следствием определения непрерывности и соответствующих свойств пределов функции.
Докажем свойство 4. Возьмем произвольное число ε > 0. Так как z = f(y) непрерывна в точке y0, то найдется число ρ(ε) > 0, такое что для всех у, принадлежащих ρ-окрестности точки y0, соответствующие значения функции f(y) принадлежат ε-окрестности числа f(y0). Так как y = ϕ(x) непрерывна в точке х0, то для найденного ρ(ε) найдется число δ(ρ(ε)) > 0 такое, что для всех х, принадлежащих δ- окрестности точки х0, соответствующие значения функции ϕ(x) принадлежат ρ-окрестности точки y0 = ϕ(x0). Итак, для произвольного ε > 0 найдется δ(ε) > 0, такое что для всех х, принадлежащих δ- окрестности точки х0, f(ϕ(x)) принадлежат ε-окрестности числа f(ϕ(x0)), т.е. сложная функция f(ϕ(x)), определенная в окрестности точки х0, непрерывна в точке х0.
2.12. Теоремы о функциях, непрерывных на отрезке
ОПРЕДЕЛЕНИЕ 2.17. Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна в каждой внутренней точке отрезка, непрерывна в точке а справа, в точке b слева.
62
Множество функций, непрерывных на [a, b], обозначается как
C[a, b].
ТЕОРЕМА 2.7. (Теорема Вейерштрасса об ограниченности непрерывной на отрезке функции.) Если f(x) C[a, b], то она ограничена на этом отрезке.
Замечания
1.Теорема не верна в случае интервала, а не отрезка. Например, функция f(x) = 1/х непрерывна на (0, 1], но не ограничена на этом интервале.
2.Теорема не верна для функции, разрывной на отрезке, например
1/ x, |
x (0, 1], |
|
f (x) = |
1, |
x = 0 |
|
||
определена на отрезке [0, 1], но не является ограниченной.
ТЕОРЕМА 2.8. (Теорема Вейерштрасса о достижимости функцией, непрерывной на отрезке, своих точных граней.) Если f(x) C[a, b], то она достигает на этом отрезке своей точной нижней и верхней грани.
Замечания
1.Теорема не верна в случае интервала, а не отрезка. Например, функция f(x) = х непрерывна на (0, 1), но не достигает на этом интервале своих точных граней.
2.Теорема не верна для функции, разрывной на отрезке. Например, функция
|
f (x) = |
x, |
x (0, 1), |
|
|
x = 0, x =1 |
|
|
|
1/ 2, |
|
определена на |
отрезке [0, 1], но |
не достигает на этом отрезке |
|
sup f (x) =1 и |
inf f (x) = 0 . |
|
|
x [0, 1] |
x [0, 1] |
|
|
|
|
|
|
ТЕОРЕМА 2.9. (Теорема Коши о нулях непрерывной на отрезке функции.) Если f(x) C[a, b] и принимает на концах отрезка значения разных знаков, то найдется точка ξ (a, b), такая что f(ξ) = 0.
Замечание. Разрывная функция, имеющая на концах отрезка значения разных знаков, может не проходить через нуль.
63
ТЕОРЕМА 2.10. (Теорема Коши о промежуточных значениях непрерывной на отрезке функции.) Если f(x) C[a,b] и f(a) = A, f(b) = B, причем А ≠ Β, то для любого числа K, лежащего между А и В, найдется точка ξ [a, b], такая что f(ξ) = K.
СЛЕДСТВИЕ. Если f(x) C[a, b], то множеством значений, принимаемых функцией на [a, b], является отрезок [m, M], где m = inf f(x), M = sup f(x).
2.13. Существование и непрерывность функции, обратной к непрерывной и строго монотонной функции
Пусть D(f) = [a, b] – область определения функции f(x), Е(f) = [c, d] – область значений функции f(x) (рис. 2.10). Если f(x) такова, что для любого у0 [c, d], уравнение
f(x) = у0
имеет единственное решение x = x0, то говорят, что функция обратима. В этом случае, выразив х из формулы у = f(x) и поменяв затем х и
уместами, получим обратную функцию f –1:
у= f –1(x) = g(x), x D(g).
y
d
y = f(x)
y0
a |
x0 |
b x |
c
Рис. 2.10. Пример графика обратимой функции
Свойства обратной функции
1. Если g – функция, обратная к f, то f – функция, обратная к g; при этом
D(g) = Е(f), Е(g) = D(f).
64
у |
|
y = х |
|
(х0, у0) |
|
|
|
|
у0 |
|
|
y = f(х) |
|
х = g(y) |
|
|
|
х0 |
|
(у0, х0) |
|
|
|
|
х0 |
|
О |
у0 |
х |
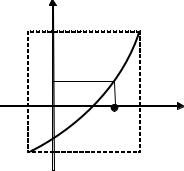
Рис. 2.11. Пример графиков взаимно обратных функций
2.g(f(x)) = x, x D(f); f(g(x)) = x, x E(f).
3.График обратной функции симметричен графику функции f(x) относительно прямой у = х. Действительно, точке (х0, f(x0)) = (х0, у0) на графике исходной функции (рис. 2.11) соответствует точка (у0, х0) на графике обратной функции.
4.Если f – строго возрастающая (строго убывающая) функция, то она обратима, причем обратная к ней функция g также является строго возрастающей (строго убывающей) функцией.
ТЕОРЕМА 2.11. Если функция y = f(x) C[a, b] и строго возрастает (убывает), то на отрезке [f(a), f(b)] определена функция x = g(y), обратная к f(x), непрерывная на [f(a), f(b)] и строго возрастающая (убывающая).
2.14. Непрерывность элементарных функций
Многочлены и дробно-рациональные функции
ТЕОРЕМА 2.12. Любой многочлен степени n
Pn(x) = anxn + … + a1x + a0, ak R k, an ≠ 0,
является непрерывной на R функцией.
Доказательство. Пусть х0 – произвольная точка числовой оси. Докажем, что
65

lim Pn (x) = Pn (x0 ).
x → x0
lim xk = lim (x x x ... x) = |
lim |
x lim |
x ... |
lim x = xk |
lim x |
|||
x → x0 |
x→x0 |
|
x → x0 |
x → x0 |
x → x0 |
0 |
x → x0 |
|
|
|
|||||||
|
|
k Ν. |
|
|
|
|
||
lim P (x) = |
lim (a xn |
+ ... + a x + a ) = a |
lim xn |
+ ... + a |
lim x + a = |
|||
n |
n |
1 |
0 |
n |
|
1 |
|
0 |
x → x0 |
x → x0 |
|
|
x → x0 |
|
x→x0 |
||
= an x0n + ... + a1x0 + a0 = P n (x0 ).
СЛЕДСТВИЕ. Всякая дробно-рациональная функция f (x) = Pn (x) ,
Qm (x)
где Pn(x) – многочлен степени n, Qm(x) – многочлен степени m, непрерывна во всех точках, в которых ее знаменатель не обращается в ноль.
Доказательство. Пусть х0 – произвольная точка числовой оси, та-
кая что Qm(x0) ≠ 0. f (x) = Pn (x) непрерывна в точке х0 как частное
Qm (x)
непрерывных функций.
Тригонометрические и обратные тригонометрические функции
ТЕОРЕМА 2.13. Функции у = sin x и y = cos x непрерывны на всей числовой оси.
Доказательство. Пусть х0 – произвольная точка числовой оси. Рассмотрим разность
|
|
|
sin x − sin x0 |
= 2sin |
x − x0 |
cos |
x + x0 |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
x − x0 |
|
|
|
x + x0 |
|
|
|
x − x0 |
|
|
|
|
|
|
||||||
sin x − sin x0 |
|
= 2 |
sin |
|
|
cos |
|
≤ 2 |
|
|
= |
|
x − x0 |
|
→ 0 при x → x0 . |
||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||
То есть
sin x →sin x0 при х → х0 .
Это значит, что у = sin x – непрерывна в точке х0. Аналогично доказывается непрерывность косинуса.
66

СЛЕДСТВИЕ. Функция y = tg x непрерывна во всех точках, кроме х = π/2 + πn; функция y = ctg x непрерывна во всех точках, кроме
х = πn.
Доказательство. Это есть следствие непрерывности синуса и косинуса и теоремы о непрерывности частного двух непрерывных функций.
ТЕОРЕМА 2.14. Обратные тригонометрические функции у = arcsin x, y = arccos x, y = arctg x, y = arcctg x непрерывны в своей области определения.
Доказательство
Функция у = arcsin x, х [–1,1] – обратная к у = sin x, х [–π/2, π/2]; функция y = arccos x, х [–1,1] – обратная к y = cos x, х [0, π]; функция y = arctg x, х R – обратная к y = tg x, х (–π/2, π/2); функция y = arcctg x, х R – обратная к y = ctg x, х (0, π).
Эти функции непрерывны в своей области определения как обратные к непрерывным функциям.
Показательная и логарифмическая функции
ТЕОРЕМА 2.15. Показательная функция у = ах, где 0 < а < 1 или а > 1, непрерывна на всей числовой оси.
Доказательство. Воспользуемся неравенством, которое приведем без доказательства:
ах – 1| < С(а) х при х → 0.
(Здесь С(а) – константа, зависящая от основания степени а.) Пусть х0 – произвольная точка числовой оси. Используя последнее
неравенство, имеем оценку
ax − ax0 = ax0 ax−x0 −1 ≤ ax0 C(a) x − x0 → 0 при х → х0 .
Отсюда следует, что и ax − ax0 → 0 при х → х0 , т.е. у = ах – непре-
рывна в точке х0.
ЗАМЕЧАНИЕ. В частности, y = ех непрерывна на всей числовой прямой. Эту функцию называют экспонентой.
ТЕОРЕМА 2.16. Логарифмическая функция y = logax, где 0 < а < 1 или а > 1, непрерывна на полуоси х > 0.
67
Доказательство. Логарифмическая функция y = logax непрерывна в своей области определения как обратная к непрерывной функции
у = ах.
Гиперболические функции
С рассмотренной выше экспонентой непосредственно связаны так называемые гиперболические функции, которые вводятся следующим образом:
|
|
e |
x |
−x |
|
|
|
y = shx = |
|
− e |
|
– гиперболический синус, |
|||
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
y = сhx = |
ex |
+ e− x |
– гиперболический косинус. |
||||
|
|
|
|
||||
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
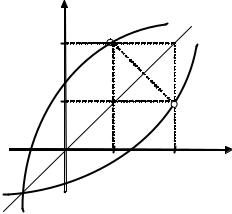
Эти функции (рис. 2.12) непрерывны на всей числовой прямой.
y = chx |
y |
|
|
1 |
|
y = 0.5e-x |
|
y = 0.5ex |
|
О |
x |
y = shx |
|
|
Рис. 2.12. Графики гиперболических функций y = shx и y = сhx
|
shx |
ex |
− e− x |
||
y = thx = |
|
= |
|
|
– гиперболический тангенс, |
|
|
|
|||
|
chx |
ex |
+ e−x |
||
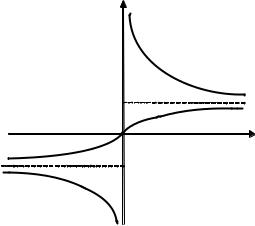
y = cthx = chx = ex + e−x – гиперболический котангенс. shx ex − e−x
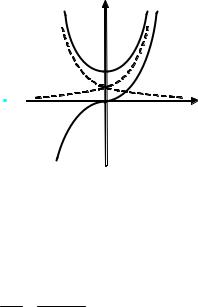
Функция y = thx непрерывна на всей числовой прямой, а y = сthx имеет разрыв второго рода в точке х = 0 (рис. 2.13).
68
y
y=cthx
1
y=thx |
О |
x |
|
–1 |
|
Рис. 2.13. Графики гиперболических функций y = thx и y = сthx
Гиперболические функции обладают рядом свойств, аналогичных соответствующим свойствам тригонометрических функций, например:
1)sh(x+у) = shx сhу + сhx shу;
2)сh(x+у) = сhx сhу + shx shу;
3)сh(2x) = сh2x + sh2x;
4)sh(2x) = 2shx сhx;
5)сh2x – sh2x = 1.
Эти свойства легко выводятся, исходя из определения гиперболических функций.
Степенная функция
ОПРЕДЕЛЕНИЕ 2.18. Пусть задано действительное число α. Функция у = хα, определенная для всех х > 0, называется степенной функцией.
ТЕОРЕМА 2.17. Степенная функция непрерывна при всех х > 0.
69
Доказательство. Из определения логарифма имеем х = elnx, следовательно, у = хα = eαlnx, т.е. степенная функция – композиция показательной и логарифмической функции, умноженной на константу. Показательная и логарифмическая функции непрерывны при х > 0, следовательно, степенная функция также непрерывна по теореме о непрерывности сложной функции.
Замечание. При рассмотрении степенной функции предполагалось, что х > 0, так как при х ≤ 0 выражение хα имеет смысл не для всех α в области действительных чисел. Однако, если α – рационально и выражение хα имеет смысл при х < 0, то функция у = хα при α > 0 будет непрерывна на всей числовой прямой, а при α < 0 – на всей действительной оси, кроме точки х = 0.
Показательно-степенная функция
Пусть функции u(x) и v(x) определены на промежутке (a, b), причем u(x) > 0 на (a, b). Тогда функцию, определяемую формулой
y = (u(x))v(x) =ev(x)lnu(x),
называют показательно-степенной.
Если функции u(x) и v(x) непрерывны на промежутке (a, b), то функция (u(x))v(x) непрерывна на (a, b) как суперпозиция непрерывных функций et и t = v(x)lnu(x).
Класс элементарных функций
К простейшим элементарным функциям обычно относят рассмотренные выше функции хα, ах, logax, sinx, cosx, tgx, сtgx, arcsinx, arccosx, arctgx, arcсtgx. Класс функций, получаемых из простейших элементарных функций с помощью конечного числа арифметических операций или путем суперпозиции этих функций, называется классом элементарных функций, а каждая функция этого класса – элементарной функцией.
Все элементарные функции непрерывны в каждой точке своей области определения.
70
