2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy

А – 1 < f(x) < А + 1.

•

Это означает ограниченность функции на множестве Uδ (a) .

Свойство 2. Если функция f(x) имеет предел в точке а, отличный от нуля, то найдется такая проколотая окрестность точки а, в которой функция сохраняет знак предела.

Доказательство. Пусть lim f (x) = А ≠ 0. По определению преде-

x→a

Если А > 0, то из левого неравенства следует, что f(x) > А/2 > 0 для

•

всех х Uδ (a). Если А < 0, то из правого неравенства следует, что

•

f(x) < А/2 < 0 для всех х Uδ (a).

Свойство 3. Если f(x) ≥ 0 в некоторой проколотой δ-окрестности точки а и lim f (x) = A, то А ≥ 0.

x →a

Доказательство. Воспользуемся определением предела по Гейне.

.

•

Возьмем числовую последовательность {xn } U δ (a) , сходящуюся к

а. Тогда lim f (xn ) = A и f(xn) ≥ 0 для всех n. Следовательно, по соот-

n →∞

ветствующей теореме для числовых последовательностей А ≥ 0.

Свойство 4. (Теорема о «зажатой» функции.) Если в некоторой проколотой δ-окрестности точки а справедливы неравенства

f(x) ≤ g(x) ≤ ϕ(x)

и существуют lim f (x) = lim ϕ(x) = A, то lim g(x) = A.

x →a x →a x →a

41

Доказательство. Воспользуемся определением предела по Гейне.

•

Возьмем числовую последовательность {хn} Uδ (a), сходящуюся к а. Тогда

lim f (xn ) = lim ϕ(xn ) = A.

Так как для всех n справедливо неравенство

f(xn) ≤ g(xn) ≤ ϕ(xn),

то по теореме о «зажатой» последовательности lim g(xn ) = A.

n →∞

Следовательно, существует lim g(x) = A.

x →a

Свойство 5. Если f(x) = с – постоянная в некоторой проколотой δ-окрестности точки а, то lim f (x) = с.

x → a

Доказательство. Воспользуемся определением предела по Гейне.

•

Возьмем числовую последовательность {xn } U δ (a), сходящуюся к а.

Доказательство. Докажем, например, в). Так как В ≠ 0, то, со-

•

гласно свойству 2, найдется U δ (a) , в которой g(x) ≠ 0. Воспользуемся определением предела по Гейне. Возьмем числовую последова-

•

тельность {xn } U δ (a), сходящуюся к а. Тогда lim f (xn ) = A,

n →∞

42

lim g(xn ) = B и по теореме о пределе частного для числовых после-

n →∞

СЛЕДСТВИЯ свойств 3, 5, 6а:

1) если f(x) ≥ В в некоторой проколотой окрестности точки а и lim f (x) = A, то А ≥ В;

x →a

2) если существует lim f (x), то для любого числа с

x →a

lim (сf (x)) = с lim f (x).

Замечание. Свойства пределов функций, сформулированные выше, остаются справедливыми и при х → а + 0, х → а − 0, х → +∞,

х→ −∞, х → ∞.

2.6.Бесконечно малые и бесконечно большие

функции

ОПРЕДЕЛЕНИЕ 2.8. Функция α(х) называется бесконечно малой при стремлении аргумента х к точке а, если lim α(x) = 0.

x →a

Замечание. Пользуясь определением предела функции в точке а и определением бесконечно малой при х → а функции, нетрудно показать, что lim f (x) = A тогда и только тогда, когда f(x) = А + α(х), где

x → a

α(х) − бесконечно малая при х → а функция.

Бесконечно малые функции обладают следующими свойствами, которые легко доказать с помощью определения предела функции по Гейне и свойств бесконечно малых числовых последовательностей:

1)алгебраическая сумма конечного числа бесконечно малых при

х→ а функций есть бесконечно малая при х → а функция;

2)произведение бесконечно малой при х → а функции на ограниченную функцию есть бесконечно малая при х → а функция.

ОПРЕДЕЛЕНИЕ 2.9. Функция f(х) называется бесконечно большой при стремлении аргумента х к точке а, если

•

ε > 0 δ(ε) > 0: x U δ (a) → f(x) > ε.

43

В этом случае пишут lim f (x) = ∞.

x → a

Аналогично определяются пределы

lim f (x) = +∞, lim f (x) = − ∞,

•

УПРАЖНЕНИЕ 2.2. Пусть α(х) ≠ 0 в U δ (a). Доказать, что функция α(х) является бесконечно малой при х → а тогда и только тогда, когда 1/α(х) – бесконечно большая при х → а функция.

Арифметика бесконечностей. Неопределенные выражения

Пусть С = const ≠ 0. Формально будем обозначать значком «∞» бесконечно большую при х → а функцию произвольного знака; «+∞» – бесконечно большую положительную при х → а функцию; «–∞» – бесконечно большую отрицательную при х → а функцию; «0» – бесконечно малую при х → а функцию; «1» – функцию, предел которой при х → а равен 1. (Здесь а – число или символы ∞, +∞, –∞.) Тогда имеют место следующие соотношения:

1.С ∞ = ∞.

2.С/0 = ∞.

3.С/∞ = 0.

4.+ ∞ + ∞ = + ∞.

5.– ∞ – ∞ = – ∞.

6.(+∞)С = + ∞, если С > 0 (0, если C < 0).

7.(+∞)+∞ = +∞.

В перечисленных ниже случаях возникают неопределенные ситуации, требующие исследования:

44

2.7. Асимптоты графика функции и способы их отыскания

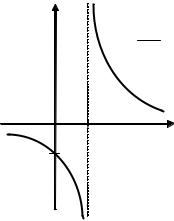
ОПРЕДЕЛЕНИЕ. 2.10. Прямая х = а называется вертикальной асимптотой графика функции у = f(x), если выполнено хотя бы одно из условий:

Например, прямая х = 1 является вертикальной асимптотой гра-

y

1

y =

x −1

–1

Рис. 2.3. Прямая х = 1 – вертикальная асимптота графика функции

ОПРЕДЕЛЕНИЕ 2.11. Прямая у = kx + b называется невертикальной асимптотой графика функции у = f(x) при х → + ∞ (при х → – ∞), если

45

Если k ≠ 0, то асимптоту называют наклонной, а если k = 0, то асимптоту у = b называют горизонтальной.

ТЕОРЕМА 2.3. (Способ отыскания наклонной асимптоты.) Прямая у = kx + b является наклонной асимптотой графика функции f(x) при х → +∞ (при х → –∞) тогда и только тогда, когда существуют конечные пределы

Доказательство

1. Пусть прямая у = kx + b – асимптота графика функции f(x) при

х → + ∞, т.е. lim ( f (x) − (kx + b)) = 0. Тогда

x → +∞

f(x) – (kx + b) = α(х), где α(х) → 0 при х→ +∞.

Отсюда получим, что при х → +∞

lim ( f (x) − kx) = b. Тогда

x → +∞

f(x) – (kx + b) = (f(x) – kx) – b = b +α(х) – b = α(х) → 0 при х→ + ∞,

т.е.

lim ( f (x) − (kx + b)) = 0.

x → +∞

Это означает, что прямая у = kx + b – асимптота графика функции f(x) при х → +∞.

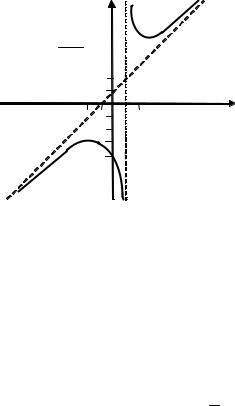
ПРИМЕР 2.3. Найти наклонные асимптоты графика функции

f(x) = x2 + 4 . x −1

46

Решение. Вычислим необходимые пределы:

Итак, прямая y = x + 1 является наклонной асимптотой графика функции при х→ +∞.

Нетрудно видеть, что аналогичная ситуация имеет место и при

х→ –∞.

y

Рис. 2.4. Прямая y = x+1 – наклонная асимптота графика функции при х → ±∞

Замечание. Для случая горизонтальной асимптоты теорема формулируется так: для того чтобы прямая y = b была асимптотой графика функции f(x) при х → +∞ (при х → –∞), необходимо и доста-

функции y = arctgx при х → +∞, а прямая y = − π – горизонтальная

2

асимптота графика функции y = arctgx при х → –∞ (рис. 2.5).

47

y

π/2

–π/2

Рис. 2.5. Эскиз график функции y = arctgx

2.8. Замечательные пределы и следствия из них

Первый замечательный предел lim sin x =1

В круге радиусом r = 1 с центром в точке О рассмотрим острый угол АОВ, хорду АВ и касательную AD к окружности в точке А (рис. 2.6). D – точка пересечения этой касательной с продолжением отрезка ОВ, С – проекция точки В на ОА.

D

В

r = 1

х

А

ОС

Рис. 2.6. Геометрический смысл неравенства sinx < x < tgx

Пусть АОВ = х радиан, где 0 < x < π/2. Тогда BC = sin x, AB = x,

DA = tg x.

Пусть S1 – площадь AOB, S2 – площадь сектора AOB, S3 – площадь AOD. Тогда

S1 < S2 < S3,

48

Следовательно, имеем неравенство

sin x < x < tg x.

Разделив на sin x > 0, получим

x

π

Последнее неравенство справедливо и для − < x < 0, так как

2

Отсюда, в частности, следует, что

sin x ≤ x , x.

Докажем, что левая часть неравенства → 1 при х → 0. Оценим разность

Следовательно, lim cos x =1.

x→0

Наконец, переходя в неравенстве

к пределу при х → 0, получаем sin x →1 при х → 0. x

49

Левая часть неравенства

Следовательно, по теореме о защемленной последовательности, имеем

Пусть х < –1. Сделаем замену х = –у. Тогда

50