
2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy
.pdf
0 ≤ xnk − ξ ≤ bk − ak .
Отсюда по теореме о «зажатой» последовательности получим, что
xnk − ξ → 0, k → ∞.
1.20. Критерий Коши существования предела последовательности
Пусть задана последовательность
x1, x2, …, xn, …, xm, …
Займемся вопросом об общем признаке существования предела этой последовательности. Само определение предела для этой цели служить не может, ибо в нем уже фигурирует тот предел, о существовании которого идет речь. Возникает необходимость признака, позволяющего решить вопрос о существовании или отсутствии предела, который использовал бы лишь значения элементов последовательности.
Поставленную задачу решает теорема, принадлежащая французскому математику О. Коши, ее называют критерием Коши сходимости последовательности. Прежде, чем заняться этой теоремой, рассмотрим понятие так называемой фундаментальной последовательности.
ОПРЕДЕЛЕНИЕ 1.7. Числовая последовательность {хn} называется фундаментальной, если она удовлетворяет условию Коши: для любого числа ε > 0 существует такое натуральное число N(ε) (зависящее от ε), что для всех n > N(ε) и m > N(ε) выполняется неравенство
хn – хm < ε.
Кратко это условие можно записать так:
ε > 0 N(ε) N: n > N(ε) и m > N(ε) → хn – хm < ε,
или в другом виде:
ε > 0 N(ε) N: n > N(ε) и p N → хn+p – хn < ε.
Замечание. Геометрический смысл фундаментальной последовательности состоит в том, что элементы такой последовательности безгранично сближаются между собой по мере возрастания их номеров.
31
ЛЕММА 1.1. Фундаментальная числовая последовательность ограничена.
Доказательство. Пусть ε = 1. В силу условия Коши найдется такой номер N(1), что для всех n > N(1) и m > N(1) выполняется неравенство
хn – хm < 1.
В частности, это неравенство выполняется для m = N + 1, т. е.
хn – хN+1 < 1.
Так как
хn = хn – хN+1 + хN+1 ≤ хn – хN+1 + хN+1 < 1 + хN+1
для всех n > N(1), то при всех n N справедливо неравенство
хn ≤ С,
где С = max{1+ хN+1 , х1 , х2 , ... , хN }. Это означает, что {хn} – ограниченная последовательность.
ТЕОРЕМА 1.13. (Критерий Коши.) Для того чтобы числовая последовательность имела предел, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство
1. Необходимость. Пусть последовательность {хn} имеет предел а. Тогда
ε > 0 N(ε) N: n > N(ε) и m > N(ε) → хn – а < ε/2, хm – а < ε/2.
Оценим модуль разности
хn – хm = хn – а + а – хm ≤ хn – а + хm – а < ε/2 + ε/2 = ε.
Следовательно, n > N(ε) и m > N(ε) выполняется неравенствохn – хm < ε, т.е. {хn} – фундаментальная последовательность.
2. Достаточность. Пусть {хn} − фундаментальна числовая последовательность. Докажем, что она имеет предел.
Согласно доказанной лемме, фундаментальная последовательность ограничена. Следовательно, по теореме Больцано – Вейерштрасса из нее можно выделить сходящуюся подпоследовательность
{ xn |
}. Пусть lim xn = a . Докажем, что а – предел исходной числовой |
|
k |
k →∞ |
k |
последовательности. Возьмем ε > 0.
32

По определению предела последовательности
|
− a |
|
< |
ε |
. |
|
N1(ε) N: k > N1(ε) → |
xn |
|
||||
|
|
|||||
|
k |
|
2 |
|
||
|
|
|
|
|
||
По определению фундаментальной последовательности
N2(ε) N: n > N2(ε) и m > N2(ε) → |
|
xn − xm |
|
< |
ε |
. |
|
|
|||||
|
|
|
||||
|
|
|
|
2 |
|
|
Пусть N(ε) = max{N1(ε), N2(ε)}. Фиксируем номер nk > N(ε). Тогда при m = nk и n > N(ε) выполняется неравенство
|
xn − xnk |
|
< |
ε |
. |
|
|
||||
|
|
|
|||
|
|
|
2 |
|
|
Таким образом, при n > N(ε) справедливо неравенство |
|||||
|
|
|
|
|
|
|
|
|
ε |
|
ε |
|
xn − a |
= |
xn − xnk + xnk − a |
≤ |
xn − xnk |
+ |
xnk |
− a |
< |
|
+ |
|
= ε . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
||
Следовательно, lim xn = a .
n→∞
ПРИМЕР 1.4. Доказать, что числовая последовательность {хn}, где
|
= |
cos1 |
+ |
cos 2 |
+ ... + |
cos n |
, n Ν , |
|||
xn |
|
|
|
|
|
|
||||
|
|
2 |
2 |
2 |
n |
|||||
|
2 |
|
|
|
|
|
|
|||
сходится.
Решение. Для того чтобы последовательность {хn} сходилась, достаточно, чтобы она была фундаментальной, т.е. удовлетворяла
условию Коши:
ε > 0 N(ε) N: n > N(ε) и p N → хn+p – хn < ε. Возьмем p N и оценим модуль разности
xn+ p − xn |
|
= |
cos(n +1) |
+ |
cos(n + 2) |
+ ... + |
cos(n + p) |
|
≤ |
|
|
||||||||
|
|
|
|
|
|||||
|
2n+1 |
2n+2 |
2n+ p |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
p |
|
|
||||||||||||||
≤ |
|
|
+ |
|
|
+ ... + |
|
|
= |
|
|
|
|
|
|
|
= |
|
|
1 − |
|
|
< |
|
|
. |
||
|
n+1 |
|
n+2 |
|
n+ p |
|
n+1 |
|
|
1 |
|
|
n |
p |
|
|||||||||||||
|
2 |
|
2 |
|
2 |
|
2 |
1 |
− |
|
|
2 |
|
2 |
2 |
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
33

Возьмем ε > 0. Найдем N(ε) N: n > N(ε) справедливо неравенство
1 < ε.
2n
Решая неравенство, получаем n > log2(1/ε). Достаточно взять N(ε) = [log2(1/ε)] + 1. Тогда
n > N(ε) и р N → хn+p – хn < ε,
т.е., согласно критерию Коши, числовая последовательность сходится.
ПРИМЕР 1.5. Доказать, что числовая последовательность {хn}, где
|
n cos(nπ) −1 |
|
xn = |
|
, n N , |
|
||
|
n |
|
расходится.
Решение. Последовательность {хn} расходится, если не выполняется условие Коши, т.е.
ε0 > 0: N0 N n ≥ N0, р N: хn+p – хn ≥ ε0.
В нашем случае
| x |
− x |
| = | cos((n + p)π) |
− cos(nπ) − |
1 |
|
+ |
|
1 |
| . |
|
|
|||||||
|
|
|
||||||||||||||||
n |
+ p |
n |
|
|
|
|
|
|
|
|
n + p |
|
|
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Например, при р = 1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| xn+1 − xn | = | cos((n +1)π) − cos(nπ) − |
|
1 |
|
|
+ |
1 |
| = | 2(−1)n+1 + |
1 |
| . |
|||||||||
|
n +1 |
|
|
|||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
n(n +1) |
|||||||
Тогда при n = 2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
| >1 , |
|
|
|||||||
| xn+1 − xn | = | x2k +1 − x2k | = | −2 + |
|
|
|
|
||||||||||||||
2k(2k +1) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а при n = 2k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| xn+1 − xn | |
= | x2k +2 − x2k +1 | = | 2 + |
|
|
1 |
|
|
| > 2 . |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
(2k + 2)(2k +1) |
|||||||||||||
То есть
ε0 = 1: n N р = 1: хn+1 – хn > 1,
и в силу критерия Коши последовательность {хn} расходится.
34
2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
2.1. Два определения предела функции в точке, их эквивалентность
В курсе математического анализа важную роль играет понятие предела, связанное с поведением функции в окрестности данной точки.
Напомним, что r-окрестностью точки а называется интервал длины 2r с центром в точке а, т.е. множество
Ur (a) = {x R : | x − a | < r}.
Если из этого интервала удалить точку а, то полученное множество называется проколотой окрестностью точки а и обозначается
•
Ur (a) . То есть
•
U r (a) = {x R : 0 < | x − a | < r}.
ОПРЕДЕЛЕНИЕ 2.1. (Определение Гейне.) Пусть функция f(x)
•
определена в Ur (a) . Число А называется пределом функции f(x) в точке а, если для любой последовательности значений ее аргумента
•
{xn } Ur (a) , сходящейся к точке а (т.е. lim xn = a ), соответствующая
n→∞
последовательность значений функции { f (xn )} сходится к А, т.е.
lim f (xn ) = A. В этом случае пишут
n→∞
lim f (x) = A
x →a
или
f(x) → А при х → а.
|
|
1 |
|
|
ПРИМЕР 2.1. Доказать, что |
f (x) = sin |
|
|
не имеет предела в |
|
||||
|
x |
|
|
|
точке х = 0.
35
Решение. Исходя из определения предела, достаточно показать,
что существуют числовые последовательности {xn |
} и {xn} с отлич- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ными от нуля элементами, сходящиеся к нулю, такие что |
|||||||||||||
lim f (xn ) ≠ lim f (xn ). |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
n→∞ |
|
|
|
|
|
|
|
|||||
Возьмем |
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
|
|
|
|||
xn = πn , |
xn = π |
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
+ 2πn |
|
|
|
|||
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
||
lim xn |
= lim xn = 0, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
n→∞ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
π |
|
|
|
||||
f (xn ) = sin(πn) = 0 n , |
f (xn ) = sin |
2 |
|
+ 2πn = 1 |
n |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f (xn ) = 0 ≠ lim |
f (xn ) =1. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n →∞ |
n →∞ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
||
Следовательно, функция f (x) = sin |
|
не имеет предела в точке |
|||||||||||
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|||
х = 0. |
|
|
|
|
|
|
|
|
|
|
|
||
ОПРЕДЕЛЕНИЕ 2.2. (Определение |
Коши.) Пусть |
функция f(x) |
|||||||||||
•
определена в Ur (a) . Число А называется пределом функции f(x) в
точке а, если для любого числа ε > 0 найдется число δ(ε) > 0, такое что для всех х, удовлетворяющих условию
0 < | x − a | < δ ,
выполняется неравенство
| f ( x) − A | < ε .
Последнее определение можно записать с помощью логических символов, используя понятие окрестностей:
•
lim f (x) = A ε > 0 δ > 0 : x U δ (a) → f ( x) Uε ( A).
x→a
36
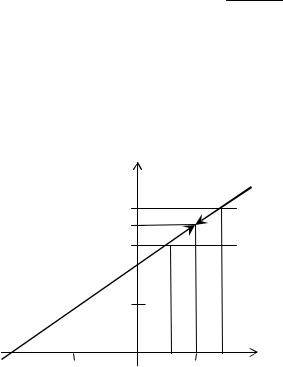
Таким образом, число А есть предел функции f(x) в точке а, если для любой ε-окрестности числа А можно найти такую проколотую δ-окрестность точки а, что для всех х, принадлежащих этой δ-окрестности, соответствующие значения функции находятся в ε-окрестности числа А.
ПРИМЕР 2.2. Исследовать функцию f (x) = x2 + x − 2 в окрест- x −1
ности точки х = 1.
Решение. Функция определена на всей числовой прямой, кроме точки х = 0.
Заметим, что f (x) = |
x2 + x − 2 |
при х ≠ 1. Построим график |
|
|
= x + 2 |
||
|
|||
|
x −1 |
|
|
функции (рис. 2.1). Видно, что при значениях аргумента, близких к 1, значения функции близки к 3.
у |
у = f(х) |
3 + ε
|
|
|
|
|
|
х |
–1 |
О |
1 – δ 1 |
1 + δ |
|||
|
||||||
Рис. 2.1. График функции |
f (x) = |
x2 + x − 2 |
||||
|
|
|
||||
|
|
|
||||
x −1
Исходя из определения предела, покажем, что lim f (x) = 3. Возьмем
x →1
ε > 0. В нашем случае достаточно взять δ = ε. Тогда для всех х, удовлетворяющих условию | x −1| < δ, x ≠ 1, выполняется неравенство
| f (x) − 3 | = | x −1| < δ = ε.
37
Итак, сформулировано два определения предела функции в точке. В дальнейшем мы будем использовать либо первое, либо второе из них, по мере необходимости. Правомерность такого обращения с определениями предела обосновывается теоремой 2.1, которую приведем без доказательства.
ТЕОРЕМА 2.1. Определения предела функции по Коши и по Гейне эквивалентны.
2.2. Критерий Коши существования предела функции
Для существования конечного предела функции f(x) при стремлении ее аргумента к точке а может быть установлен такой же признак, как и в случае числовой последовательности.
ТЕОРЕМА 2.2. Для того чтобы функция f(x), определенная в некоторой проколотой окрестности точки а, имела предел в точке а, необходимо и достаточно, чтобы она удовлетворяла условию Коши:
|
|
• |
|
|
|
ε > 0 δ > 0 : |
′ ′′ |
U δ (a) → |
′ |
′′ |
< ε. |
x , x |
f ( x ) − f ( x ) |
||||
2.3. Пределы функции в точке слева и справа
Введем следующие обозначения:
• |
|
|
|
|
Ur− (a) = {x: a − r < x < a} |
– |
левая |
проколотая |
полуокрестность |
точки а, |
|
|
|
|
• |
|
|
|
|
Ur+ (a) = {x: a < x < a + r} |
– |
правая |
проколотая |
полуокрестность |
точки а. |
|
|
|
|
|
|
|
|
• |
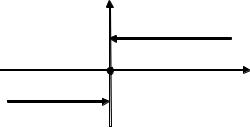
ОПРЕДЕЛЕНИЕ 2.3. Пусть функция f(x) определена в Ur− (a).
Число А1 называется пределом слева функции f(x) в точке а и обозначается
lim f (x) (или f(а – 0)),
x → a − 0
если
ε > 0 δ(ε) > 0: х (а – δ, a) → f(x) – A1< ε.
38
•
ОПРЕДЕЛЕНИЕ 2.4. Пусть функция f(x) определена в Ur+ (a).
Число А2 называется пределом справа функции f(x) в точке а и обозначается
lim f (x) (или f(а + 0)),
x → a + 0
если
ε > 0 δ(ε) > 0: х (а, a+δ) → f(x) – A2< ε.
Например, для функции (рис. 2.2)
−1, |
если |
x < 0, |
|
|
|
|
x = 0, |
f (x) = signx = 0, |
если |
||
|
1, |
если |
x > 0, |
|
|||
в точке х = 0 определены односторонние пределы
lim f (x) = f (−0) = −1 , |
lim f (x) = f (+0) =1. |
x → − 0 |
x → + 0 |
yy = signx
1
О |
x |
–1
Рис. 2.2. График функции y = signx (знак числа х)
УПРАЖНЕНИЕ 2.1. Доказать, что для существования lim f (x)
x →a
необходимо и достаточно, чтобы существовали пределы этой функции в точке а слева и справа и
lim f (x) = lim f (x).
x → a − 0 |
x → a + 0 |
39
2.4.Пределы функции при стремлении аргумента
кбесконечности
Напомним следующие обозначения интервалов на числовой оси:
Ur(+∞) = (r, +∞) = {x R: x > r}, Ur(–∞) = (–∞, –r) = {x R: x < – r},
Ur(∞) = Ur(+∞) Ur(–∞) = {x R: |x| > r}.
ОПРЕДЕЛЕНИЕ 2.5. Пусть функция f(x) определена в Ur(+∞). Число А называется пределом функции f(x) при х → + ∞, если
ε > 0 δ(ε) > 0: х (δ, +∞) → f(x) – A < ε.
В этом случае пишут lim f (x) = A.
x → + ∞
ОПРЕДЕЛЕНИЕ 2.6. Пусть функция f(x) определена в Ur(–∞). Число А называется пределом функции f(x) при х → –∞, если
ε > 0 δ(ε) > 0: х (–∞, –δ) → f(x) – A < ε.
В этом случае пишут lim f (x) = A.
x → − ∞
ОПРЕДЕЛЕНИЕ 2.7. Пусть функция f(x) определена в Ur(∞). Число А называется пределом функции f(x) при х → ∞, если
ε > 0 δ(ε) > 0: х (–∞, –δ) (δ, +∞) → f(x) – A < ε.
В этом случае пишут lim f (x) = А.
x →∞
2.5. Свойства функций, имеющих предел
Функция, имеющая конечный предел в заданной точке, обладает некоторыми локальными свойствами, т.е. свойствами, справедливыми в окрестности этой точки.
Свойство 1. Если функция f(x) имеет предел в точке а, то найдется такая проколотая окрестность точки а, в которой функция ограничена.
Доказательство. Пусть lim f (x) = А. По определению предела,
x →a
для заданного числа ε = 1 найдется число δ > 0, такое что для всех
•
х Uδ (a) , выполняется неравенство f(x) – A < 1, или
40
