2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy

больших последовательностей не всегда является бесконечно большой. Например:

Аналогичная ситуация имеет место при вычислении lim xn , если

n→∞ yn

обе последовательности бесконечно малые.

1.13. Неопределенные выражения

0

ленность типа .

0

Если xn → 0, yn → ∞ при n → ∞, то выражение {xn yn} представляет собой неопределенность типа (0 ∞). Теорема о пределе произведения в этом случае неприменима.

Если xn → +∞, yn → − ∞ при n → ∞, то выражение {xn + yn} представляет собой неопределенность типа (∞ − ∞). В этом случае не работает теорема о пределе суммы (разности).

Вычисление пределов в случае неопределенных выражений называется раскрытием неопределенностей.

1.14. Предельный переход в неравенствах

ТЕОРЕМА 1.6. (О сохранении пределом знака элементов после-

довательности.) Пусть lim xn = a, причем xn ≥ 0 n N. Тогда а ≥ 0.

n→∞

21

Доказательство. Предположим противное: а < 0 (рис. 1.11). Так как а – предел числовой последовательности, то вне любой окрестности этого числа может содержаться лишь конечное число элементов последовательности. Выберем ε так, чтобы Uε(a) (–∞, 0). Но, по условию теоремы, все элементы последовательности лежат на положительной полуоси, т.е. вне Uε(a) находится бесконечно много ее элементов, что противоречит определению предела. Следовательно, а ≥ 0.

Рис. 1.11. К теореме 1.6 о сохранении пределом знака элементов последовательности

СЛЕДСТВИЕ ТЕОРЕМЫ 1.6. Если lim xn = a , причем xn ≤ 0

n→∞

n N, то а ≤ 0.

ТЕОРЕМА 1.7. (О сохранении элементами последовательности

знака ее предела.) Пусть lim xn = a, причем а > 0. Тогда найдется

n→∞

такое натуральное число N, что xn > 0 для всех n > N. Доказательство. Возьмем ε = а/2. Тогда, согласно определению

предела, найдется N(ε) N, такое что для всех n > N будет выполнено неравенство

хn – а < а/2,

которое эквивалентно системе неравенств

а/2 < хn < 3а/2.

То есть xn > 0 для всех n > N (рис. 1.12).

хn, n > N

Рис. 1.12. К теореме 1.7 о сохранении элементами последовательности знака ее предела

22

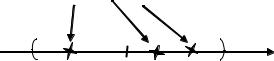
ТЕОРЕМА 1.8. (О пределе «зажатой» последовательности.) Если числовые последовательности {хn}, {уn}, {zn} таковы, что

хn ≤ уn ≤ zn для всех n ≥ N0,

lim xn = lim zn = a,

n→∞ n→∞

то последовательность {уn} сходится и

lim yn = a.

n→∞

Доказательство. Возьмем ε > 0.

lim xn = a, следовательно, по определению предела, найдется

n→∞

N1(ε), такое что хn Uε(a) n > N1(ε).

lim zn = a, следовательно, найдется N2(ε), такое что zn Uε(a) для

n→∞

n > N2(ε).

Возьмем N(ε) = max{N0, N1(ε), N2(ε)}. Тогда уn Uε(a) для n > N(ε) (рис. 1.13), т.е. {уn} сходится и lim yn = а.

n→∞

хn ≤ уn ≤ zn, n > N

а – ε а а + ε

Рис. 1.13. К теореме 1.8 о пределе «зажатой» последовательности

Замечание. Эту теорему называют теоремой о трех последовательностях, или теоремой о «зажатой» последовательности, или (до недавнего времени) теоремой «о двух милиционерах».

Доказательство. По теореме о пределе разности

хn – уn → а – b,

при этом, по условию теоремы,

хn – уn ≥ 0.

23

Тогда по теореме о сохранении пределом знака членов последовательности имеем

a – b ≥ 0,

т.е. a ≥ b.

1.15. Существование предела у ограниченной монотонной последовательности

(свойство Вейерштрасса)

Числовая последовательность {xn} называется возрастающей (строго возрастающей), если n N справедливо неравенство

хn+1 ≥ хn (хn+1 > хn).

Аналогично последовательность {xn} называется убывающей (строго убывающей), если n N справедливо неравенство

хn+1 ≤ хn (хn+1 < хn ).

Возрастающую или убывающую числовую последовательность называют монотонной, а строго возрастающую или строго убывающую – строго мнотонной.

Например, {1/n} – строго убывающая последовательность, {n} – строго возрастающая последовательность, последовательность {sin n} не является монотонной.

Ранее были даны понятия точной верхней и нижней грани числового множества. Теперь сформулируем понятия точных граней в случае, если числовое множество – множество значений числовой последовательности {xn}.

ОПРЕДЕЛЕНИЕ 1.5. Число а называется точной верхней (нижней) гранью числовой последовательности {xn} (рис. 1.14), если

1)xn ≤ а (xn ≥ а) n;

2)ε > 0 N(ε): xN > a – ε (xN < a + ε).

xN

Рис. 1.14. К определению точной верхней грани числовой последовательности

24

ТЕОРЕМА 1.10. (Свойство Вейерштрасса.) Всякая возрастающая, ограниченная сверху числовая последовательность {xn} имеет предел, причем

lim xn = sup{xn}.

n→∞

Всякая убывающая, ограниченная снизу числовая последовательность имеет предел, причем

lim xn = inf{x n}.

n→∞

Доказательство. Докажем теорему для первого случая. Если последовательность {xn} ограничена сверху, т.е. множество чисел х1, х2, …, хn, … ограничено сверху, то существует точная верхняя грань этой последовательности. Пусть а = sup{xn}. Покажем, что

lim xn = а.

n→∞

Зафиксируем ε > 0. Так как а = sup{xn}, то, согласно определению

точной верхней грани, xn ≤ а n и N(ε): xN > a – ε.

Так как {xn} – возрастающая последовательность, то для всех n ≥ N(ε) получим следующие неравенства:

a – ε < xN ≤ xn ≤ а ≤ а + ε.

Поэтому для всех n ≥ N(ε) выполняется неравенство хn – а| < ε. Это и означает, согласно определению предела, что

lim xn = а = sup{ xn }.

n→∞

1.16. Число е

Рассмотрим последовательность {xn}, где

Покажем, что эта последовательность сходится. Для этого достаточно доказать, что она возрастает и ограничена сверху.

Воспользуемся формулой бинома Ньютона:

(a + b)n = Cn0an + Cn1an−1b + Cn2an−1b2 + ... + Cnn−1abn−1 + Cnnbn ,

25

Заметим, что при переходе от n к n + 1 число слагаемых в сумме увеличивается на 1 и, кроме того, каждое слагаемое увеличивается:

Поэтому хn < хn+1 для всех n N, т.е. {xn} – строго возрастающая последовательность.

26

Далее заметим, что имеет место оценка

n

Кроме того, для любых k N справедливо неравенство

Используя приведенные выше оценки и формулу для суммы геометрической прогрессии, получаем

т.е. {xn} ограничена сверху. Согласно свойству Вейерштрасса, такая последовательность имеет предел. Этот предел обозначается буквой е. Таким образом,

Таким образом, установлено, что для всех n N справедливо неравенство

переходя к пределу в котором, получим оценку для числа е:

2 < e < 3.

Более точными оценками можно установить, что справедливо приближенное равенство:

е ≈ 2,718281828459045.

Доказано также, что число е иррационально и, более того, трансцендентно, т.е. не является корнем никакого алгебраического уравнения с целыми коэффициентами. Число е играет в математическом анализе особую роль. Оно, в частности, является основанием натуральных логарифмов.

27

1.17. Принцип вложенных отрезков

ОПРЕДЕЛЕНИЕ 1.6. Система числовых отрезков [a1, b1], [a2, b2], …, [an, bn], …, где an R, bn R, n N, называется системой вложенных отрезков, если

a1 ≤ a2 ≤ … an ≤ … ≤ bn ≤ … ≤ b2 ≤ b1,

т.е. если каждый следующий отрезок [an+1, bn+1] содержится в предыдущем.

ТЕОРЕМА 1.11. Для всякой системы вложенных отрезков с длинами, стремящимися к нулю, существует единственная точка ξ, принадлежащая всем отрезкам данной системы, причем

ξ = sup{an} = inf{bn}.

Доказательство. Последовательность левых концов отрезков {an} возрастает и ограничена сверху, например числом b1. Тогда по свой-

ству Вейерштрасса существует lim an = sup{a n} = α. По свойству

n→∞

верхней грани an ≤ α n. Последовательность правых концов отрезков {bn} убывает и ограничена снизу, например числом а1. Тогда по

свойству Вейерштрасса существует lim bn = inf{bn} = β. По свойству

n→∞

нижней грани bn ≥ β n. С другой стороны, bn = an + (bn – an),

откуда, переходя к пределу, получим

lim bn = lim an + lim(bn − an ) = α + 0.

n→∞ n→∞ n→∞

Следовательно, α = β = ξ и an ≤ ξ ≤ bn n. То есть существует точка, принадлежащая всем отрезкам одновременно. Покажем, что такая точка единственна. Предположим, что существует еще одна точка ξ1 [an, bn] n. Тогда

0 ≤ ξ – ξ1 ≤ bn – an → 0 при n → ∞.

Следовательно, по теореме о «зажатой» последовательности получим ξ = ξ1.

28

1.18. Подпоследовательность числовой последовательности. Частичные пределы последовательности

Пусть дана числовая последовательность {xn}. Рассмотрим строго возрастающую последовательность натуральных чисел {nk}, т.е. такую, что

n1 < n2 < n3 < … < nk < …

Тогда последовательность {уk} = {xnk } {xn } называется подпоследовательностью числовой последовательности {xn}. Например:

1)последовательность нечетных чисел 1, 3, 5, 7, 9, …, взятых в порядке возрастания, является подпоследовательностью последовательности натуральных чисел 1, 2, 3, 4¸ …;

2)последовательность 3, 5, 1, 9, 11, 7, … есть подмножество множества натуральных чисел. Однако она не является подпоследовательностью последовательности 1, 2, 3, 4¸…, так как нарушен порядок членов (рис. 1.15).

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …

Рис. 1.15. Пример подмножества множества натуральных чисел,

не являющегося подпоследовательностью

Согласно определению, подпоследовательность {xnk }образована

из членов исходной последовательности {xn}, причем порядок следования элементов в подпоследовательности такой же, как и в последовательности {xn}. В записи {xnk } число k означает порядковый номер

элемента последовательности xn1 , xn2 , ..., а xnk − номер этого элемен-

та в исходной последовательности. Поэтому nk ≥ k , откуда следует,

что nk → ∞ при k → ∞.

Введем понятие частичного предела последовательности. Пусть {xnk } − подпоследовательность последовательности {xn}. Если су-

29

тельности {xn}. Например, последовательность {1 + (–1)n} имеет два частичных предела, а именно 0 и 2.

Если {xn} − ограниченная последовательность, а L – множество ее частичных пределов, то числа sup L и inf L называют соответственно верхним и нижним пределом этой последовательности и обозначают

соответственно символами lim xn и lim xn .

n→∞ n→∞

Например, последовательность 1, 2, 3, 1, 2, 3, 1, 2, 3, … имеет

lim xn = 3 , lim xn =1.

n→∞ n→∞

1.19. Существование частичного предела у ограниченной последовательности. Теорема Больцано – Вейерштрасса

ТЕОРЕМА 1.12. (Больцано – Вейерштрасса.) Из всякой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность.

Доказательство. Пусть {xn} – ограниченная числовая последовательность, тогда существуют числа a, b, такие, что a ≤ xn ≤ b n N. Разделим отрезок [a, b] точкой на две равные части. Тогда, по крайней мере, одна из частей содержит бесконечное число элементов числовой последовательности. Обозначим [a1, b1] правую половину, если в ней содержится бесконечное число элементов последовательности, и левую – в противном случае. Выберем xn1 [a1, b1 ] .

Разделим отрезок [a1, b1] точкой на две равные части. Обозначим [a2, b2] правую половину, если в ней содержится бесконечное число элементов последовательности, и левую – в противном случае. Вы-

Тогда по принципу вложенных отрезков существует единственная точка ξ [ak, bk], k. Так как расстояние между ξ и xnk не превосходит длины отрезка [ak, bk], имеем оценку

30