2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy

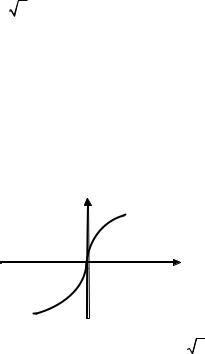
ПРИМЕР 3.12. Найти направления выпуклости и точки перегиба графика функции y = 3 х .

Решение. Вычислим производные первого и второго порядка:

Здесь y ′(x) → ∞ при х → 0 и график функции в точке х = 0 имеет вертикальную касательную. Вторая производная в точке х = 0 не определена, а при переходе через эту точку меняет знак с плюса на минус. Итак, точка х = 0 – точка перегиба. Направление выпуклости функции в соответствии со знаками второй производной показано на рис. 3.9.

y

y ″ < 0

О x

y ″ > 0

Рис. 3.9. Фрагмент графика функции y = 3 х

3.22. Общая схема исследования и построения графика функции одной переменной

Изучение заданной функции f(x) и построение ее графика целесообразно проводить в следующем порядке:

1.Найти область определения функции.

2.Выяснить, является ли функция четной, нечетной, периодической.

3.Найти точки пересечения графика с осями координат и промежутки, на которых f(x) > 0 и f(x) < 0.

4.Найти асимптоты графика.

5.Сделать приблизительный эскиз графика.

6.Вычислить первую производную, найти точки экстремума и промежутки возрастания (убывания) функции.

7.Вычислить вторую производную, найти точки перегиба и промежутки выпуклости вверх или вниз функции.

8.Окончательно вычертить график.

111

ПРИМЕР 3.13. Провести полное исследование функции

f (x) =

x3

(1 + x)2

и построить ее график.

Будем действовать по приведенной выше схеме. 1. Область определения функции

D(f) = (–∞, –1) (– 1, + ∞).

2.Функция общего вида.

3.Найдем нули функции, решив уравнение

f(x) = 0 x = 0.

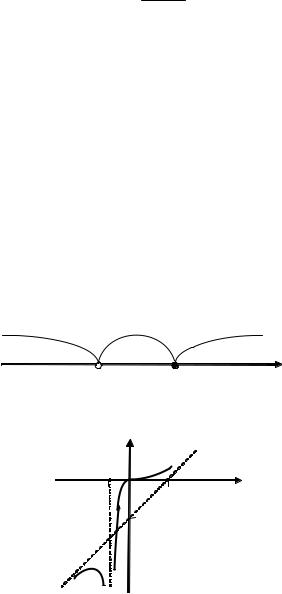
Отметим на числовой прямой промежутки знакопостоянства функции (рис. 3.10).

4.Найдем асимптоты графика функции, вычислив необходимые пределы. В результате получим:

х= – 1 – вертикальная асимптота;

у= х – 2 – наклонная асимптота как при х → – ∞, так и при х → + ∞.

5.На основе полученной информации построим приблизительный эскиз графика (рис. 3.11).

Рис. 3.10. Промежутки знакопостоянства функции f(x)

y = x – 2

y

– 2

Рис. 3.11. Эскиз графика функции f(x), построенный без применения производных

112

6. Вычислим первую производную функции

f ′(x) = x2 (x + 3) . (1 + x)3

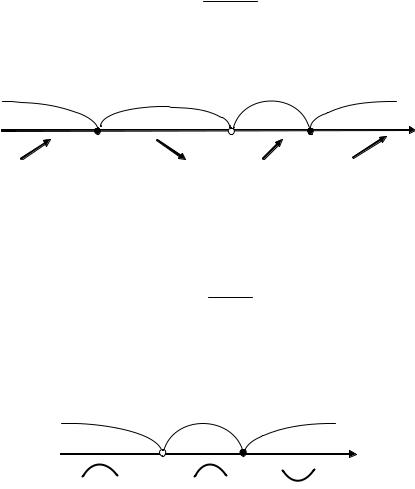
Найдем критические точки производной и отметим их на числовой прямой. Расставим знаки производной в полученных интервалах и укажем направления возрастания-убывания функции (рис. 3.12).

Рис. 3.12. Знаки первой производной и промежутки возрастанияубывания функции f(x)

Вычислим значение функции в обнаруженной точке максимума: f(–3) = – 27/4.

7. Найдем вторую производную функции

6x

f ''(x) = (1 + x)4 .

Отметим на числовой прямой критические точки второй производной. Расставим знаки f′′ (x) в полученных интервалах и укажем направления выпуклости функции (рис. 3.13).

Точка

перегиба

х

–1 0

Рис. 3.13. Знаки второй производной и направления выпуклости графика функции f(x).

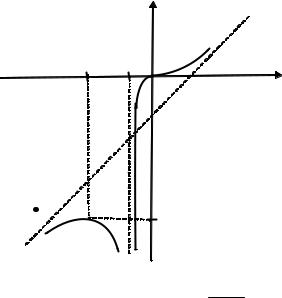
8. Окончательно построим график (рис. 3.14).

113

y

y = x – 2

–6,75

3

Рис. 3.14. График функции y =

x

(1 + x)2

114

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Ильин В.А., Позняк Э.Г. Основы математического анализа. – М.: ФИЗМАТЛИТ, 2005. – Ч. 1.

Кудрявцев Л.Д. Курс математического анализа. – М.: Дрофа, 2008. – Т. 1.

Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа. – М.: ФИЗМАТЛИТ, 2003.

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: ФИЗМАТЛИТ, 2001. – Т. 1.

115

Учебное издание

Разумейко Борис Григорьевич Ким-Тян Луиза Ревмировна Недосекина Ирина Сергеевна

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Курс лекций

Редактор И.Е. Оратовская

Компьютерная верстка И.Г. Иваньшина

Национальный исследовательский технологический университет «МИСиС», 119049, Москва, Ленинский пр-т, 4

Издательский Дом МИСиС, 119049, Москва, Ленинский пр-т, 4 Тел. (495) 638-45-22

Отпечатано в типографии Издательского Дома МИСиС 119049, Москва, Ленинский пр-т, 4 Тел. (499) 236-76-17, тел./факс (499) 236-76-35

116