2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy

Часто бывает удобно для разложений функций f(x) и g(x) использовать готовый набор разложений элементарных функций по формуле Маклорена. Для этого в случае, когда x0 ≠ 0, следует предварительно сделать замену переменной, положив t = x – x0. Тогда t → 0 при x → x0.

Случай x → ∞ сводится заменой переменной x = 1/t к случаю t → 0.

∞

Если имеется неопределенность вида ∞ , то ее легко привести к

0

рассмотренному случаю с помощью преобразования

0

f (x) = 1/ g(x) . g(x) 1/ f (x)

При применении метода выделения главной части к раскрытию неопределенностей вида (0·∞) и (∞ – ∞) их следует преобразовать к

0

неопределенности вида .

0

Для раскрытия неопределенностей вида 00, ∞0, 1∞ данным методом необходимо предварительно прологарифмировать рассматриваемые функции.

ПРИМЕР 3.4. Найти lim sin x − x .

x→0 x3

Решение. В данном случае нам предстоит раскрытие неопреде-

0

ленности Разложим числитель дроби по формуле Маклорена:

0

101

приведя дроби к общему знаменателю. Теперь задача сводится к вычислению предела

lim sin2 x − x2 .

x→0 x2 sin2 x

Разложим по формуле Маклорена до первого отличного от нуля слагаемого числитель и знаменатель дроби:

Решение. В данном случае дана неопределенность вида (1∞). Сделаем необходимые преобразования:

Теперь функция в показателе степени при х→ 0 представляет собой неопределенность вида (∞ 0). Разложим эту функцию по формуле Маклорена:

102

Следовательно:

3.19. Приложения формулы Тейлора

кисследованию поведения функции

вокрестности точки

Вкачестве примера применения формулы Тейлора для исследования поведения функции в окрестности точки приведем доказательство третьего достаточного условия экстремума, использующего производные высших порядков.

ТЕОРЕМА 3.16. (Третье достаточное условие экстремума.) Пусть у функции f(x) существует f (n)(x0), где n > 2, и выполняются условия:

f ´(x0) = f ´´(x0) = … = f (n–1)(x0) = 0, f (n)(x0) ≠ 0.

Тогда

а) если n = 2k, то x0 – точка локального экстремума функции, а именно, точка строгого локального минимума, если f(n)(x0) > 0, и точка строгого локального максимума, если f(n)(x0) < 0;

б) если n = 2k + 1, то x0 – не является точкой экстремума функции. Доказательство. Применяя формулу Тейлора, получаем

f ( x) = f ( x0 ) + f (n) ( x0 ) ( x − x0 )n + о(( x − x0 )n ), х → х0 . n!

Отсюда имеем

Если n = 2k, то (х – х0)n > 0 и разность f(x) – f(x0) имеет знак производной, т.е.

f(x) < f(x0), если f (n)(x0) < 0, и х0 – точка локального максимума, f(x) > f(x0), если f (n)(x0) > 0, и х0 – точка локального минимума. Если n = 2k + 1, то (x – x0)n имеет разные знаки в левой и правой

полуокрестности точки x0, т.е. разность f(x) – f(x0) меняет знак при переходе через точку x0. Это означает, что эта точка не является точкой экстремума.

103

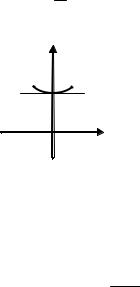
ПРИМЕР 3.7. Исследовать поведение функции y = cos x + chx в

окрестности точки x0 = 0.

Решение. Здесь

x0 = 0 является точкой локального минимума функции (рис. 3.6). Значение функции в этой точке f(0) = 2. Разложение функции по формуле Маклорена имеет вид

f (x) = 2 + 2 x4 + o(x4 ) .

3.20. Правило Лопиталя раскрытия неопределенностей

При вычислении предела отношения f (x) при х → a в случае, g(x)

когда обе функции являются бесконечно малыми либо бесконечно большими, иногда удобно применять правило, позволяющее заменять предел отношения функций пределом отношения их производных. Это правило обычно называют правилом Лопиталя.

104

ТЕОРЕМА 3.17. Пусть функции f(x) и g(x) дифференцируемы на интервале (a, b) и удовлетворяют условиям:

Тогда существует предел

lim f (x) = A .

x→a+0 g(x)

Доказательство. В силу условий теоремы функции f(x) и g(x) не определены в точке a. Доопределим их в точке a, положив f(a) = g(a) = 0. Тогда на отрезке [a, х] для доопределенных таким образом функций выполнены условия теоремы Коши, т.е.

Если х → a + 0, то ξ→ a + 0 и в силу условия теоремы существует

lim f '(ξ) = A . x→a+0 g '(ξ)

Поэтому и

lim f (х) = A .

x→a+0 g(х)

ТЕОРЕМА 3.18. Пусть функции f(x) и g(x) дифференцируемы при х > а и удовлетворяют условиям

1) lim f (x) = lim g(x) = 0;

x→+∞ x→+∞

2) g'(x) ≠ 0 для всех х > а;

105

Тогда существует и

lim f (x) = A .

x→+∞ g(x)

Доказательство. Можно считать, что a > 0. Положим x = 1/t. Эта функция отображает (а, +∞) на (0, 1/а). После сделанной замены переменной можно применить предыдущую теорему:

ЗАМЕЧАНИЕ. Правило Лопиталя раскрытия неопределенности вида остается справедливым также при х → a – 0, при х → a, при х → – ∞, при х → ∞.

ТЕОРЕМА 3.19. Пусть функции f(x) и g(x) дифференцируемы на интервале (a, b) и удовлетворяет условиям

1) f (x) = ∞ , g(x) = ∞ ;

2) g'(x) ≠ 0 для

3) существует Тогда существует

lim f (x) = A .

x→a+0 g(x)

ЗАМЕЧАНИЕ. Правило Лопиталя раскрытия неопределенности остается справедливым также при х → a – 0, при х → a, при

х → + ∞, при х → – ∞, при х → ∞.

106

Другие виды неопределенностей

Чтобы применить правило Лопиталя для раскрытия неопределенностей

Для раскрытия неопределенностей вида 00, ∞0, 1∞, нужно предварительно прологарифмировать соответствующие функции.

ПРИМЕР 3.8. Доказать, что

lim ln x = 0 , если a > 0.

a

x→+∞ x

Решение. Применяя правило Лопиталя раскрытия неопределен-

ПРИМЕР 3.9. Доказать, что

lim xа = 0, если a > 0.

x→+∞ ех

Решение. Пусть m = [a] + 1, тогда a – m < 0. Применяя m раз пра-

∞

вило Лопиталя раскрытия неопределенности вида , получаем

∞

Замечание. Приведенные выше примеры показывают, что при х → +∞ логарифмическая функция растет медленнее степенной функции, а степенная функция растет медленнее показательной.

ПРИМЕР 3.10. Доказать, что

lim xа ln x = 0 , если a > 0.

107

3.21. Условия выпуклости и условие существования точек перегиба графика функции

Направление выпуклости графика функции

Пусть функция f(x) дифференцируема в любой точке интервала (а, b). Тогда существует касательная к графику функции, проходящая через любую точку М(x, f(x)) этого графика, причем эта касательная не параллельна оси Оу.

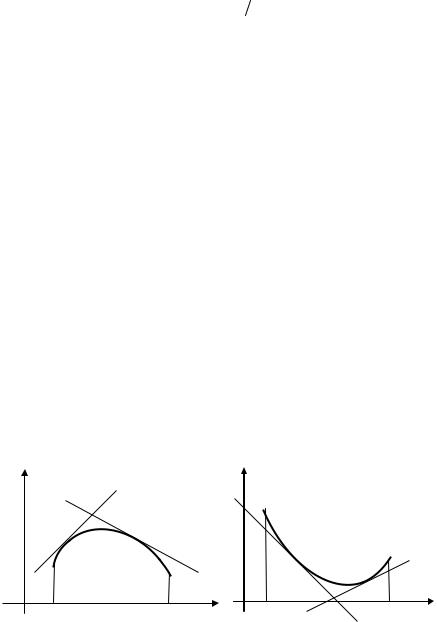
ОПРЕДЕЛЕНИЕ 3.8. График функции f(x) имеет на интервале (а, b) выпуклость, направленную вверх (вниз), если в пределах этого интервала он расположен не выше (не ниже) любой своей касательной (рис. 3.7).

Рис. 3.7. Выпуклость вверх и вниз графиков функции

108

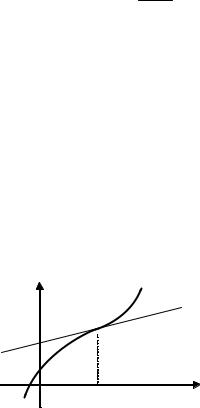
ТЕОРЕМА 3.20. Если функция f(x) имеет на интервале (а, b) вторую производную и f ′′(x) ≤ 0 ( f ′′(x) ≥ 0) во всех точках интервала, то график функции имеет на (а, b) выпуклость, направленную вверх (вниз).

Доказательство. Пусть f ′′(x) ≤ 0 на (а, b). Возьмем произвольную точку x0 (а, b). Уравнение касательной к графику функции в точке М(x0, f(x0)) имеет вид

Укас = f(x0) + f ′(x0)(x – x0).

Запишем для f(x) формулу Тейлора первого порядка в окрестности точки х0:

f (x) = f (x0 ) + f ′(x0 )(x − x0 ) + f ′′(ξ) (x − x0 )2 . 2

Отсюда следует, что

во всех точках интервала, т.е. график лежит не выше касательной.

Точки перегиба графика функции

ОПРЕДЕЛЕНИЕ 3.9. Точка М(х0, f(x0)) называется точкой перегиба графика функции у = f(x), если в этой точке график имеет касательную и существует окрестность точки х0 оси Ох, в пределах которой слева и справа от х0 график функции имеет разные направления выпуклости (рис. 3.8).

y = f(x)

y

М(х0, f(x0)) y0

Рис. 3.8. Точка перегиба графика функции

109

ТЕОРЕМА 3.21. (Необходимое условие перегиба.) Если М(x0, f(x0)) − точка перегиба графика функции у = f(x) и функция имеет в этой точке непрерывную вторую производную, то f ′′(x0) = 0.

Доказательство. Предположим, что f ′′(x0) ≠ 0. Тогда в силу непрерывности f ′′(x) ≠ 0 в некоторой окрестности точки x0. Следовательно, функция сохраняет направление выпуклости в этой окрестности, что противоречит определению точки перегиба.

ТЕОРЕМА 3.22. (Первое достаточное условие перегиба.) Пусть функция у = f(x) непрерывна в точке x0, дважды дифференцируема в окрестности этой точки и график функции имеет касательную в точке М(x0, f(x0)). Если в пределах этой окрестности f ′′(x) имеет разные знаки слева и справа от x0, то М(x0, f(x0)) – точка перегиба графика функции.

Доказательство. Так как f ′′(x) имеет разные знаки слева и справа от x0, то направление выпуклости слева и справа от точки различно, т.е. М(x0, f(x0)) – точка перегиба графика функции.

ТЕОРЕМА 3.23. (Второе достаточное условие перегиба.) Если f ′′(x0) = 0, а f (3)(x0) ≠ 0, то x0 – точка перегиба графика функции у = f(x).

Доказательство. Запишем для f(x) соответствующую рассматриваемому случаю формулу Тейлора третьего порядка в окрестности точки х0:

Выражение в правой части последнего равенства имеет разные знаки слева и справа от точки x0, т.е. при переходе через точку x0 график функции меняет направление выпуклости и М(x0, f(x0)) – точка перегиба графика функции.

110