2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy

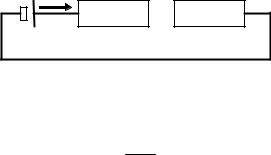
Аналогичными средствами решается вопрос об отыскании максимального и минимального значений функции на интервале, полупрямой, бесконечной прямой (при условии, что это значение существует).

Может случиться, что функция f(x) не имеет на отрезке [a, b] (или полупрямой [a, +∞)) точек возможного экстремума. В таком случае она является монотонной на этом отрезке (полупрямой), и ее максимальное и минимальное значения достигаются на концах этого отрезка (на конце этой полупрямой). Проиллюстрируем последний случай физическим примером.

Пусть требуется определить, какое сопротивление х нужно включить в цепь последовательно с данным сопротивлением r, чтобы на r выделилась наибольшая мощность, при этом напряжение u0 батареи считается постоянным. Схема электрической цепи приведена на рис. 3.4.

u0 I

Рис. 3.4. Схема электрической цепи

По закону Ома ток I в цепи равен

I = u0 . r + x

Следовательно, по тому же закону падение напряжения ur на сопротивлении r равно

Таким образом, мощность w(x), выделяемая на сопротивлении r, равна

Так как по физическому смыслу сопротивление х не может быть отрицательным, то задача сводится к отысканию наибольшего значения функции w(x) на полупрямой [0, +∞). Вычислим производную этой функции

91

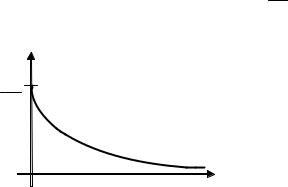
Нетрудно заметить, что w ′(x) < 0 всюду на полупрямой [0, +∞) и точек возможного экстремума нет. Таким образом, функция w(x) (рис. 3.5) убывает всюду на полупрямой [0, +∞) и ее максимальное

2

значение на этой полупрямой достигается при х = 0 и равно u0 . Это r

ясно и из физических соображений.

у

2

u0

r

у = w(x)

Рис. 3.5. Зависимость мощности w, выделяемой на сопротивлении r, от включенного последовательно с ним сопротивления х

3.16. Формула Тейлора

Пусть функция f(x) имеет в точке х0 производную n-го порядка. Этой функции поставим в соответствие многочлен степени n следующего вида:

Этот многочлен называется многочленом Тейлора степени n функции f(x) в точке х0.

Заметим, что

Tn ( x0 ) = fn ( x0 ), Tn′( x0 ) = fn′( x0 ), Tn′′( x0 ) = fn′′(x0 ), ... , Tn(n) (x0 ) = f (n) (x0 );

Tn(k ) (x0 ) = 0, k > n.

92

ОПРЕДЕЛЕНИЕ 3.7. Формула вида

f(x) = Tn(x) + Rn(x)

называется формулой Тейлора n-го порядка функции f(x) в точке х0. Здесь функция Rn(x), представляющая собой разность между функцией и ее многочленом Тейлора, называется n-м остатком Тейлора.

Приведем примеры формулы Тейлора.

1. Формула конечных приращений Лагранжа

f(х) = f(х0) + f ′(ξ)(х – х0),

где ξ – точка, лежащая между х и х0. Это формула Тейлора нулевого порядка с остатком в форме Лагранжа, где

T0(x) = f(х0), R0(x) = f ′(ξ)(х – х0).

2.Если f(х) дифференцируема в точке х0, то ее можно представить

ввиде

f(х) = f(х0) + f ′(х0)(х – х0)+ о(х – х0).

Это формула Тейлора первого порядка с остатком в форме Пеано, где

T1(x) = f(х0) + f ′(х0)(х – х0), R1(x) = о(х – х0).

3. Из таблицы эквивалентных бесконечно малых имеем, что

1 – cosx ~ x2/2 при х → 0,

т.е.

cosx = 1 – x2/2 + o(x2).

Это формула Тейлора второго порядка с остатком в форме Пеано, где

х0 = 0, T2(x) = 1 – x2/2, R2(x) = о(х2).

ТЕОРЕМА 3.13. (Формула Тейлора с остатком в форме Лагранжа.) Пусть функция f(x) (n + 1) раз дифференцируема в Uδ(x0). Тогда для f(x) справедлива формула Тейлора n-го порядка в точке х0, причем

Rn (x) = f (n+1) (ξ) (x − x0 )n+1 , (n +1)!

где ξ – точка, лежащая между х и х0.

93

Доказательство. Пусть для определенности x > x0. Обозначим

Rn(x) = f(x) – Tn(x). В силу свойств многочлена Тейлора, имеем

Rn(x0) = R'n(x0) = Rn''(x0) = … = Rn(n)(x0) = 0,

Rn(n+1)(x) = f (n+1)(x) для всех х Uδ(x0). Введем вспомогательную функцию

g(x) = (x – x0)n+1.

Заметим, что

g(x0) = g'(x0) = g''(x0) = … = g(n)(x0) = 0,

g(n+1)(x) = (n+1)! для всех х Uδ(x0).

Применим к функциям Rn(x) и g(x) обобщенную формулу конечных приращений Коши (n + 1) раз:

откуда следует утверждение теоремы.

ТЕОРЕМА 3.14. (Формула Тейлора с остатком в форме Пеано.) Пусть функция f(x) n раз дифференцируема в Uδ(xо) и f(n)(x) непрерывна в точке х0. Тогда при х → х0 функция может быть представлена в виде

94

Доказательство. Так как f(x) n раз дифференцируема в Uδ(x0), то для нее справедлива формула Тейлора с остатком в форме Лагранжа порядка (n – 1)

откуда следует утверждение теоремы.

ТЕОРЕМА 3.15. (Единственность представления функции в виде многочлена по степеням (х – х0).) Пусть функция f(x) n раз дифференцируема в Uδ(x0) и f (n)(x) непрерывна в точке х0. Если при х→ х0 функция представима в виде

f ( x) = a0 + a1 ( x − x0 ) + a2 ( x − x0 )2 + ... + an ( x − x0 )n + o(( x − x0 )n ),

то

Доказательство. Для функции выполнены условия предыдущей теоремы, тогда

95

a0 + a1 ( x − x0 ) + a2 ( x − x0 )2 + ... + an ( x − x0 )n + o((x − x0 )n ) =

Переходя к пределу при х→ х0 в обеих частях равенства, получаем

a0 = f(x0).

Отбросим равные члены и поделим на x – x0. Переходя к пределу при х→ х0, получаем

a1 = f '(x0)

и так далее.

Итак, единственным многочленом наилучшего приближения для функции f(x) при х→ х0 является ее многочлен Тейлора.

3.17. Разложение основных элементарных функций по формуле Тейлора

Если х0 = 0, то формула Тейлора с остатком в форме Пеано принимает вид

(Напомним, что по определению полагают f(0)(x) = f(x), 0! = 1.) Замечание. Если в формуле Тейлора х0 = 0, ее называют форму-

лой Маклорена.

Получим разложения по формуле Тейлора в окрестности точки х0 = 0 основных элементарных функций.

1)f(x) = ех. Здесь f (k)(x) = ex, k = 1, 2, … . Поэтому f(0) = 1, f (k)(0) = 1

иформула Тейлора для функции ех записывается в виде

96

или

2) f(x) = sin x. Здесь f (k)(x) = sin(x + kπ/2), k = 0, 1, 2, … . Следовательно:

f (2m)(0) = sin(mπ) = 0, f (2m+1)(0) = sin(π/2 + mπ) = (–1)m, m = 0, 1, 2, … и формула Тейлора для функции sinx записывается в виде

или

3) f(x) = cos x. Здесь f (k)(x) = cos(x + kπ/2), k = 0, 1, 2, … . Следовательно:

f (2m)(0) = cos(mπ) = (–1)m, f (2m+1)(0) = cos(π/2 + mπ) = 0, m = 0, 1, 2, … и формула Тейлора для функции cosx записывается в виде

4) f (x) = ln(1 + x). Здесь f (k)(x) = (–1)k–1(k – 1)!(1 + x)–k. Следовательно: f(0) = 0, f (k)(0) = (–1)k–1(k – 1)!, k = 1, 2, …

и формула Тейлора для рассматриваемой функции записывается в виде

97

5) f(x) = (1 + x)α. В данном случае f (k)(x) = α(α – 1)(α – 2)…(α – k + 1)× ×(1+x)α – k . То есть

f(0) = 0, f (k)(0) = α(α – 1)(α – 2) … (α – k + 1)

и формула Тейлора записывается в виде

или

Это частный случай предыдущей формулы. Однако при получении разложения мы использовали формулу для суммы бесконечно убывающей геометрической прогрессии.

7) f (x) = 1 =1 − x + x2 −... + (−1)n xn + o(xn ), х → 0 . 1 + x

Разложение получено из предыдущей формулы путем замены х на –х.

ПРИМЕР 3.2. Разложить по формуле Тейлора в окрестности точки х0 = 0 функцию

f (x) = 3 1 + x5 .

1

Решение. Запишем функцию в виде f (x) = (1 + x5 )3 . Применим

формулу

в которой при α = 1 заменим х на х5. В результате получим

3

98

ПРИМЕР 3.3. Разложить по формуле Тейлора в окрестности точки х0 = 0 функцию

f(x) = ln x − 5 .

x− 3

Решение. Преобразуем функцию следующим образом:

пользуемся формулой

в которой в первом случае заменим х на − x , а во втором – на − x :

99

В результате получим

3.18. Вычисление пределов с помощью формулы Тейлора

Формула Тейлора дает простое и общее правило для выделения главной части функции при вычислении пределов.

В этом случае рекомендуется разложить по формуле Тейлора функции f(x) и g(x) в окрестности точки x0 (если это возможно), ограничившись в этом разложении лишь первыми не равными нулю членами, т.е. взять разложения в виде

f(x) = a(x – x0)n + o((x – x0)n), a ≠ 0,

g(x) = b(x – x0)m + o((x – x0)m), b ≠ 0,

тогда

100