
- •1. Развитие представлений о природе света.
- •2. Понятие о когерентности электромагнитных волн.
- •3. Интерференция света. Условие интерферентности волн.
- •4. Методы наблюдения интерференции света. Метод Юнга.
- •6. Расчет интерференциоии от 2-х источников света
- •5. Методы наблюдения интерференции света. Зеркала Френеля.
- •7. Интерференция в тонких пленках.
- •8. Ннтерференционные приборы и их применение.
- •9. Принцип Гюйгенса-Френеля.
- •10. Метод зон Френеля.
- •11. Явление дифракции. Дифракция Френеля на круглом отверстии.
- •Дифракция френеля на круглых отверстиях
- •12. Явление дифракции. Дифракция Френеля на непрозрачном диске.
- •14. Дифракционная решетка. Главные и дополнительные максимумы и минимумы.
- •15. Расчет формулы дифракционной решетки
- •16. Применение дифракционной решетки. Разрешающая способность.
- •Применение явлений д-ии света
- •17. Дифракция рентгеновских лучей.
- •18 .Основы голограмм.
- •19. Дисперсия света.
- •33. Квантовая теория Планка. Формула Планка.
- •20. Электронная теория дисперсии света.
- •21. Поглощение света. Закон Бугера.
- •В прозрачных изотропных средах и в кристаллах куб. Системы может возникать двойной луч преломления под влиянием внеш. Воздейс–й, в частности это происходит при мех. Дифор. Тв. Тел.
- •27. Вращение плоскости поляризации. Эффект Фарадея.
- •28. Тепловое излучение и его характеристики.
- •29. Закон Кирхгофа для равновесного излучения.
- •30 Абсолютно черное тело. Закон Стефана-Больцмана.
- •72. Ядерные реакции и законы сохранения.
- •31. Абсолютно черное тело. Закон смещения Вина.
- •32. Абсолютно черное тело. Формула Релея-Джинса.
- •34. Внешний фотоэффект и его законы.
- •35. Уравнение Эйнштейна для внешнего фотоэффекта.
- •36. Модель атома Резерфорда и ее недостатки.
- •37. Закономерности в спектре излучения атома водорода.
- •38. Постулаты Бора. Модель атома Бора.
- •39. Корпускулярно-волновой дуализм свойств вещества.
- •44. Уравнение Шредингера для стационарных состояний.
- •40. Волны де Бройля и их свойства.
- •41. Соотношение неопределенности Гейзенберга.
- •42. Волновая функция и её статический смысл.
- •43. Общее уравнение Шредингера нерелятивистской квантовой механики
- •45. Прохождение частицы через потенциальный барьер.
- •46. Решение уравнения Шредингера для водородоподобных атомов
- •47. Квантовые числа, их физический смысл.
- •49. Спин электрон. Спиновое квантовое число.
- •48. Пространственное распределение электрона в атоме водорода.
- •50. Принцип Паули. Распределение электронов в атоме по состояниям.
- •55. Спонтанное и вынужденное излучение фотонов.
- •51. Периодическая система Менделеева.
- •52. Рентгеновские спектры. Природа сплошного и характеристического рентгеновских спектров.
- •73. Реакция деления ядер.
- •53. Физическая природа химической связи в молекулах. Понятие об энергетических уровнях.
- •54. Колебательные и вращательные спектры молекул.
- •56. Принцип работы квантового генератора.
- •57. Твердотельные и газоразрядные лазеры. Их применение.
- •58. Фононы. Теплоемкость кристаллической решетки.
- •59. Элементы зонной теории в кристаллах.
- •60. Энергетические зоны в кристаллах. Валентная и зона проводимости.
- •61. Заполнение зон: диэлектрики, проводники, полупроводники по зонной теории.
- •63. Основы квантовой теории электропроводимости металла. Сверхпроводимость.
- •66. Электронные и дырочные полупроводники.
- •62. Понятие о квантовой статистике Ферми-Дирака. Уровень Ферми.
- •64. Собственная проводимость полупроводников.
- •65. Примесная проводимость полупроводников.
- •67. Контакт электронного и дырочного полупроводников …
- •68. Строение атомных ядер. Массовое и зарядовые числа. Нуклоны.
- •69. Взаимодействие нуклонов. Свойства и природа ядерных сил.
- •71. Правила смещения. Α-распад. Взаимопревращения …
- •70. Естественная радиоактивность. Закон радиоактивного распада.
- •75. Термоядерная реакция и проблемы её управления.
- •76. Элементарные частицы. Космическое излучение. …
- •74. Цепная реакция деления ядер. Ядерный реактор.
14. Дифракционная решетка. Главные и дополнительные максимумы и минимумы.
Д![]()
![]() ифракционная
решетка – совокупность щелей одинаковой
ширины, разделенных одинаковыми
непрозрачными промежутками. Решетки
бывают прозрачными и отражательными.
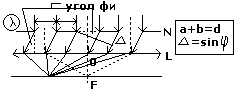
Рассмотрим оптическую схему действия
прозрачной дифракционной решетки. Пусть
плоская монохромная волна падает
нормально на дифракционную решетку,
состоящую изN
щелей шириной а, разделенными промежутками
b.
a+b
– период решетки (постоянная решетки)
d,
т.к. волна падает нормально, то волновой
фронт достигает плоскостей всех щелей
одновременно => все щели испускают
вторичные волны в одинаковой фазе.
Выделим вторичные волны, идущие под
углом φ к плоскостям щелей. Они соберутся
в некоторой точке р экрана. Если бы
волны, идущие от различных щелей, были
некогерентны, то результирующая картина
на экране не отличалась бы от картины,
наблюдаемой при дифракции на одной
щели. Лишь все интенсивности возросли
бы в N(c.2)
раз. A=Nai;
J=N(c.2)Ji.
Однако вторичные волны, идущие от
различных щелей когерентны, и это
усложняет результирующую картину на
экране, т.к. кроме интерференции вторичных
волн, идущих от каждой точки внутри
каждой щели, будет иметь место интерференция
N
дифрагированных волн, идущих от различных
щелей. Иными словами, кроме дифракции
на одной щели будет интерференция N
дифрагированных пучков. Для нахождения
условия max
и min
на экране, воспользуемся графическим
методом, для этого разобьем открываемую
щелями часть волнового фронта на малые
параллельные лучам участки, и обозначим
вектор амплитуду, испускаемую таким
малым участком, a(в)i.
Тогда A(в)=Σ
[по I
щели] a(в)i+Σ
[по II
щели] a(в)i+…+Σ
[по N
щели] a(в)i=A1(в)+A2(в)+…+AN(в),
где Ai(в)
– вектор амплитуды в точке р всей i-ой
щелью. Модули вект. |Ai(в)|
одинаковы и определяются углом дифракции
φ. Каждый последующий вектор повернут
по отношению к предыдущему на угол δ,
равный разности фаз, создаваемых в точке
р колебаниями от 2-х соседних щелей.
Разность фаз ∆ определяется разностью
хода ∆=dsinφ.
Очевидно, что min
интенсивности на экране останется на
тех же местах, что и при дифракции на
одной щели, ибо те направления, вдоль
которых ни одна щель света не посылает,
не получит его и при N
щелях. Т.о. условие min
– asinφ=kλ
(1), сохраняется и при дифракции на многих
щелях. (1) – условие min,
которое носит название главного или
прежнего. Если разность фаз δ от 2-х
соседних щелей равна нулю, то все векторы
ai(в)
(и Ai(в))
располагаются вдоль одной линии. =>
∆=dsinφ=0
(2) (т.к. δ=2π∆/λ).
Т.о. условие (2) – условие главного max
(или нулевого) в точке р будет всякий
раз и тогда, когда разность фаз между
соседними колебаниями δ=+ - 2kπ,
k=1,2,3.
В этом случае все векторы ai(в)
располагаются вдоль одной прямой. Т.о.
условие + - 2kπ=2π∆/λ,
dsinφ=+
- kλ
(3), где k=0,1,2,
есть условие главных max
на экране. Min
в точке р будут всякий раз тогда
ифракционная
решетка – совокупность щелей одинаковой
ширины, разделенных одинаковыми
непрозрачными промежутками. Решетки
бывают прозрачными и отражательными.
Рассмотрим оптическую схему действия
прозрачной дифракционной решетки. Пусть
плоская монохромная волна падает
нормально на дифракционную решетку,
состоящую изN
щелей шириной а, разделенными промежутками
b.
a+b
– период решетки (постоянная решетки)
d,
т.к. волна падает нормально, то волновой
фронт достигает плоскостей всех щелей
одновременно => все щели испускают
вторичные волны в одинаковой фазе.
Выделим вторичные волны, идущие под
углом φ к плоскостям щелей. Они соберутся
в некоторой точке р экрана. Если бы
волны, идущие от различных щелей, были
некогерентны, то результирующая картина
на экране не отличалась бы от картины,
наблюдаемой при дифракции на одной
щели. Лишь все интенсивности возросли
бы в N(c.2)
раз. A=Nai;
J=N(c.2)Ji.
Однако вторичные волны, идущие от
различных щелей когерентны, и это
усложняет результирующую картину на
экране, т.к. кроме интерференции вторичных
волн, идущих от каждой точки внутри
каждой щели, будет иметь место интерференция
N
дифрагированных волн, идущих от различных
щелей. Иными словами, кроме дифракции
на одной щели будет интерференция N
дифрагированных пучков. Для нахождения
условия max
и min
на экране, воспользуемся графическим
методом, для этого разобьем открываемую
щелями часть волнового фронта на малые
параллельные лучам участки, и обозначим
вектор амплитуду, испускаемую таким
малым участком, a(в)i.
Тогда A(в)=Σ
[по I
щели] a(в)i+Σ
[по II
щели] a(в)i+…+Σ
[по N
щели] a(в)i=A1(в)+A2(в)+…+AN(в),
где Ai(в)
– вектор амплитуды в точке р всей i-ой
щелью. Модули вект. |Ai(в)|
одинаковы и определяются углом дифракции
φ. Каждый последующий вектор повернут
по отношению к предыдущему на угол δ,
равный разности фаз, создаваемых в точке
р колебаниями от 2-х соседних щелей.
Разность фаз ∆ определяется разностью
хода ∆=dsinφ.
Очевидно, что min
интенсивности на экране останется на
тех же местах, что и при дифракции на
одной щели, ибо те направления, вдоль
которых ни одна щель света не посылает,
не получит его и при N
щелях. Т.о. условие min
– asinφ=kλ
(1), сохраняется и при дифракции на многих
щелях. (1) – условие min,
которое носит название главного или
прежнего. Если разность фаз δ от 2-х
соседних щелей равна нулю, то все векторы
ai(в)
(и Ai(в))
располагаются вдоль одной линии. =>
∆=dsinφ=0
(2) (т.к. δ=2π∆/λ).
Т.о. условие (2) – условие главного max
(или нулевого) в точке р будет всякий
раз и тогда, когда разность фаз между
соседними колебаниями δ=+ - 2kπ,
k=1,2,3.
В этом случае все векторы ai(в)
располагаются вдоль одной прямой. Т.о.
условие + - 2kπ=2π∆/λ,
dsinφ=+
- kλ
(3), где k=0,1,2,
есть условие главных max
на экране. Min
в точке р будут всякий раз тогда![]() ,
когда ломанная из векторов Ai(в)
превращается в замкнутую ломанную.
Вект. AN(в)
образует с осью отсчета ОХ угол δN.
δN=+
- 2kπ
– он будет параллелен оси ОХ.
,
когда ломанная из векторов Ai(в)
превращается в замкнутую ломанную.
Вект. AN(в)
образует с осью отсчета ОХ угол δN.
δN=+
- 2kπ
– он будет параллелен оси ОХ.
δ =+
- (2kπ)/N;
+ - (2kπ)/N=+
- (2π∆)/λ
(1), ∆=+ - kλ/N;
dsinφ=
+ - kλ/N
(4), k≠N,2N,3N…,
т.к. minàmax.
(4) опредлеляет положение на экране min,
которые называются добавочными. Между
2-мя добавочными min
находится добвочные max,
интенсивность которых мала. При этом
сопоставление (3) и (4) соотношений
позволяет увидеть, что между 2-мя главными
max,
будет (N-1)
добавочный min,
и (N-2)
добавочный max.
=+
- (2kπ)/N;
+ - (2kπ)/N=+
- (2π∆)/λ
(1), ∆=+ - kλ/N;
dsinφ=
+ - kλ/N
(4), k≠N,2N,3N…,
т.к. minàmax.
(4) опредлеляет положение на экране min,
которые называются добавочными. Между
2-мя добавочными min
находится добвочные max,
интенсивность которых мала. При этом
сопоставление (3) и (4) соотношений
позволяет увидеть, что между 2-мя главными
max,
будет (N-1)
добавочный min,
и (N-2)
добавочный max.
