
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
1.4 Скалярное поле. Производная по направлению. Градиент
Предположим,
что в каждой точке М
некоторой области D
задано
значение
скалярной
величины
![]() ,
т. е. такой
величины, которая полностью
характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом
,
т. е. такой
величины, которая полностью
характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом
![]() называют скалярной функцией точки и
записывают
называют скалярной функцией точки и
записывают![]() .
.
ОПРЕДЕЛЕНИЕ. Если
в области D
задана скалярная функция точки
![]() ,
то говорят, что в этой области задано
скалярное поле.
,
то говорят, что в этой области задано
скалярное поле.
Если
скалярное поле отнесено к системе
координат
![]() ,
то задание точкиМ
равносильно
заданию ее координат
,
то задание точкиМ
равносильно
заданию ее координат
![]() .
.
Поверхностью
уровня
скалярного поля называют геометрическое
место точек, в которых функция
![]() принимает постоянное значение, т. е.
принимает постоянное значение, т. е.![]() ,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.
,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.
Пусть
задано скалярное поле, т. е. задана
функция
![]() .
Возьмем точку
.
Возьмем точку![]() и некоторое направление
и некоторое направление![]() ,
определяемое направляющими косинусами
,
определяемое направляющими косинусами![]() .
При перемещении в данном направлении
точки
.
При перемещении в данном направлении
точки![]() в точку
в точку![]() функция
функция![]() получает приращение
получает приращение
![]() ,
,
которое
называют приращением функции в данном
направлении. Величину перемещения точки
![]() обозначим через
обозначим через![]() ,
тогда можно записать, что
,
тогда можно записать, что
![]() .
.
ОПРЕДЕЛЕНИЕ. Производной
функции
![]() в направлении
в направлении![]() называют предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю
называют предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю
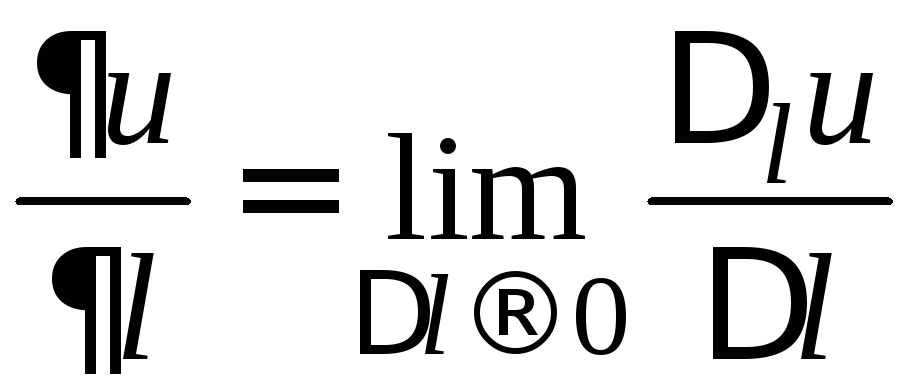 .
.
Вычислить производную по направлению можно, используя следующую теорему:
ТЕОРЕМА. Если
функция
![]() дифференцируема, то ее производная
дифференцируема, то ее производная![]() по любому направлению
по любому направлению![]() существует и равна
существует и равна
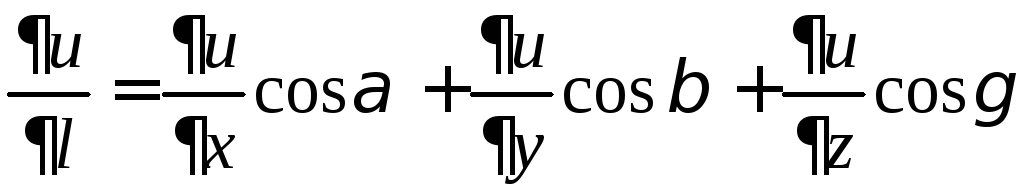 ,
,
где
![]() -
направляющие косинусы направления
-
направляющие косинусы направления![]() .
.
ПРИМЕР. Найти
производную функции
![]() в точке
в точке![]() по направлению, идущему от точки
по направлению, идущему от точки![]() к точке
к точке![]() .
.
РЕШЕНИЕ
Найдем
единичный вектор e,
соответствующий направлению
![]() :
:
![]() ,
,
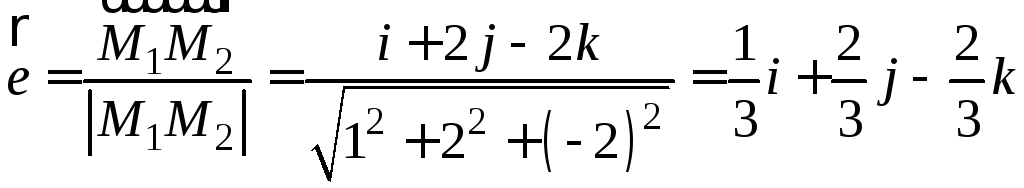 ,
,
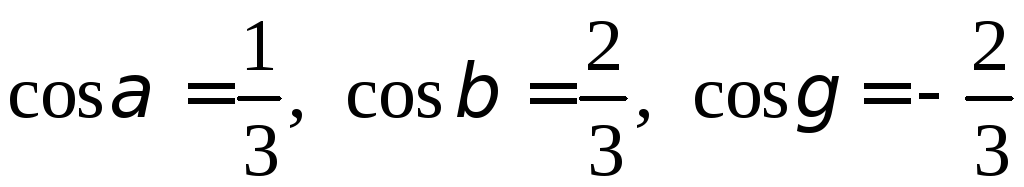 .
.
Частные
производные функции
![]() равны:
равны:
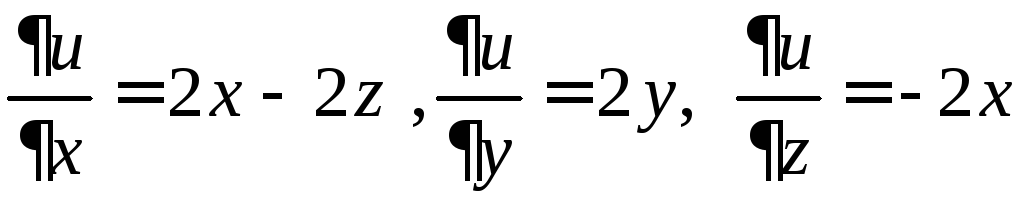 .
.
Вычислим
частные производные в точке
![]() и найдем производную по направлению из
равенства
и найдем производную по направлению из
равенства
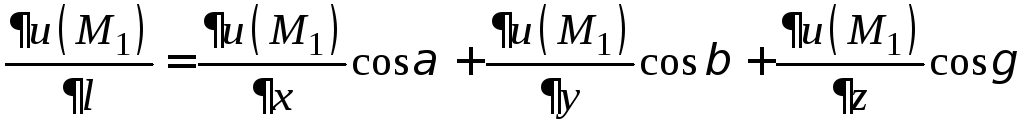 ,
,
получим
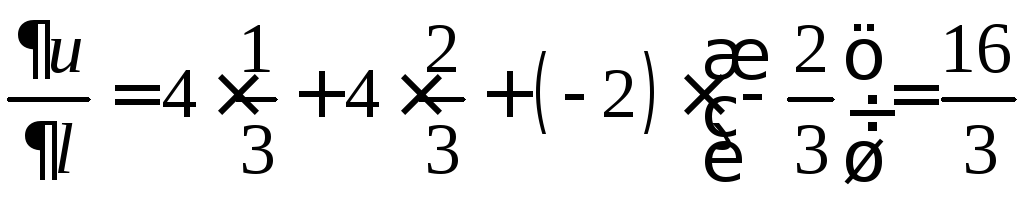 .
.
ОПРЕДЕЛЕНИЕ. Градиентом
функции
![]() называют вектор, проекциями которого
служат значения частных производных
этой функции, т. е.
называют вектор, проекциями которого
служат значения частных производных
этой функции, т. е.
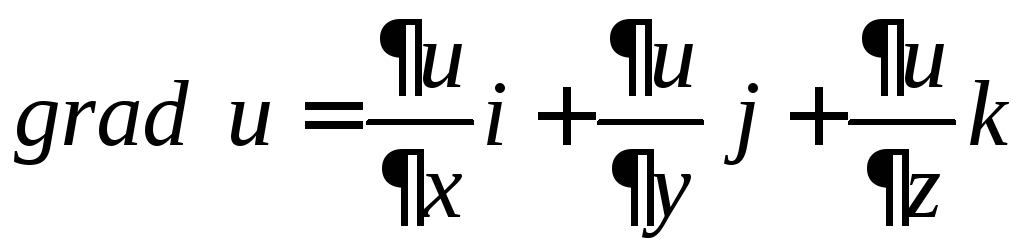 .
.
Используя определение градиента, формулу производной по направлению можно записать в виде:
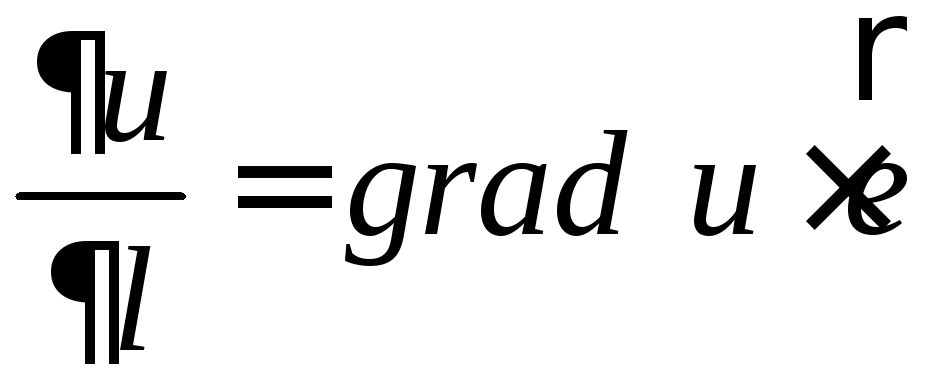 ,
,
где
![]() - единичный вектор направления
- единичный вектор направления![]() .
.
Меняя
направление
![]() ,
мы будем получать различные значения
производной
,
мы будем получать различные значения
производной![]() ,
причем наибольшее значение наблюдается,
когда направление
,
причем наибольшее значение наблюдается,
когда направление![]() совпадает с вектором
совпадает с вектором![]() .
Таким образом,
.
Таким образом,![]() определяет направление, в котором
скорость возрастания функции
определяет направление, в котором
скорость возрастания функции![]() является
наибольшей.
является
наибольшей.
Градиент скалярного поля в данной точке по величине и направлению равен максимальной скорости изменения поля в данной точке.
ПРИМЕР. Дано
скалярное поле
![]() .
Составить уравнение линии уровня
.
Составить уравнение линии уровня![]() .
Вычислить с помощью градиента производную
скалярного поля в точке
.
Вычислить с помощью градиента производную
скалярного поля в точке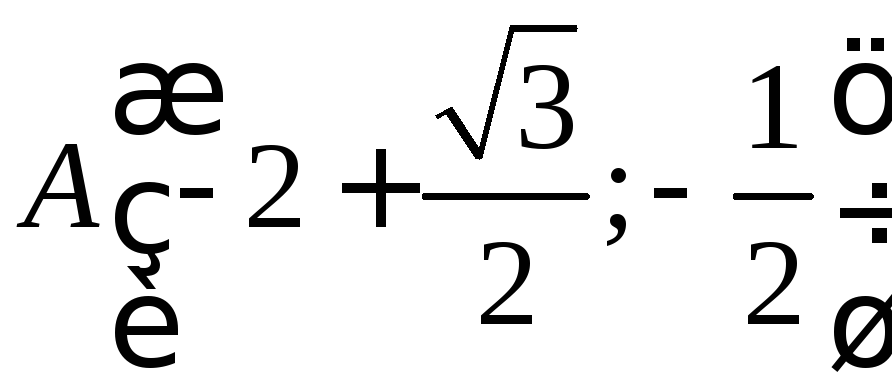 по направлению вектора
по направлению вектора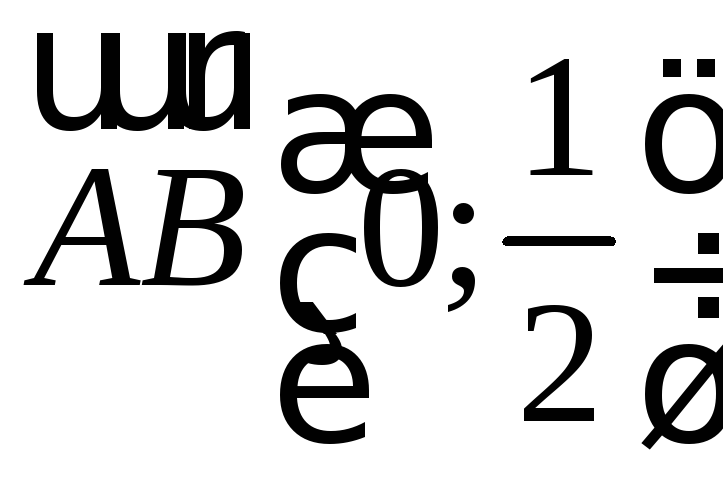 .
Найти наибольшую скорость изменения
скалярного поля в точке
.
Найти наибольшую скорость изменения
скалярного поля в точке![]() .
.
РЕШЕНИЕ
Поверхностью
уровня (линией уровня) данного скалярного
поля является окружность с центром в
точке
![]() ,
радиуса 1:
,
радиуса 1:
![]() ,
,
![]() .
.
Градиент
функции равен: ![]() .
.
Найдём
единичный вектор направления
![]() :
: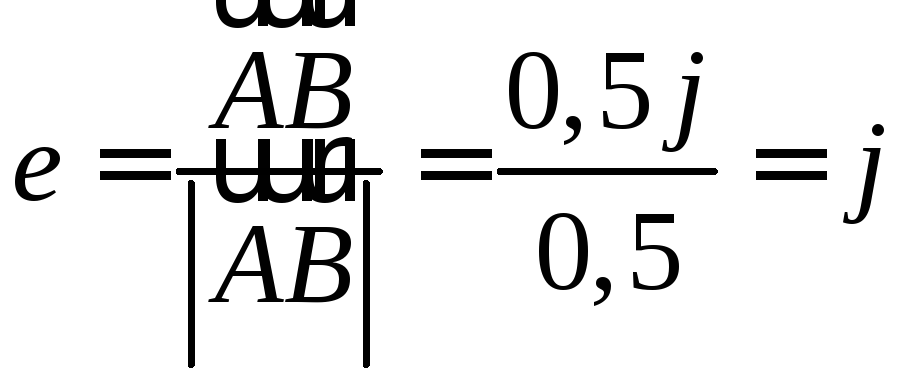 ,
а затем производную скалярного поля
,
а затем производную скалярного поля![]() по направлению
по направлению![]() в точке
в точке![]() :
:
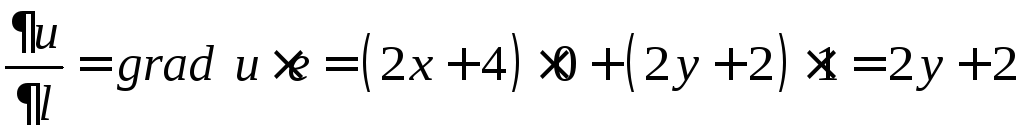 ,
,
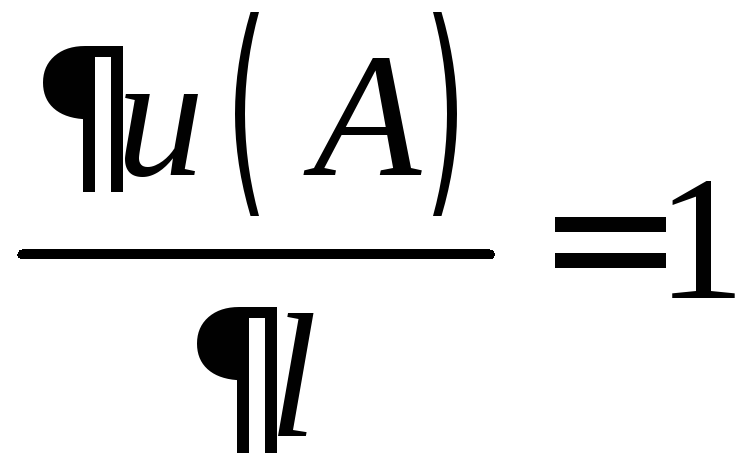 .
.
Так
как
 ,
то данное скалярное поле возрастает по
направлению вектора
,
то данное скалярное поле возрастает по
направлению вектора![]() со скоростью равной 1.
со скоростью равной 1.
Теперь
найдём производную по направлению
![]() :
:
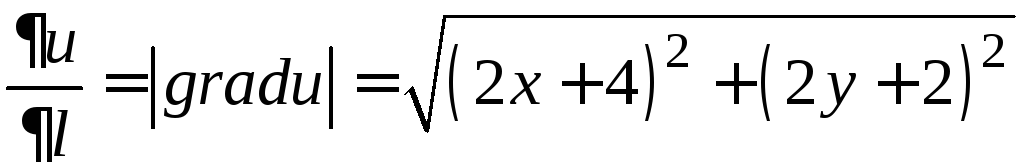 ,
,
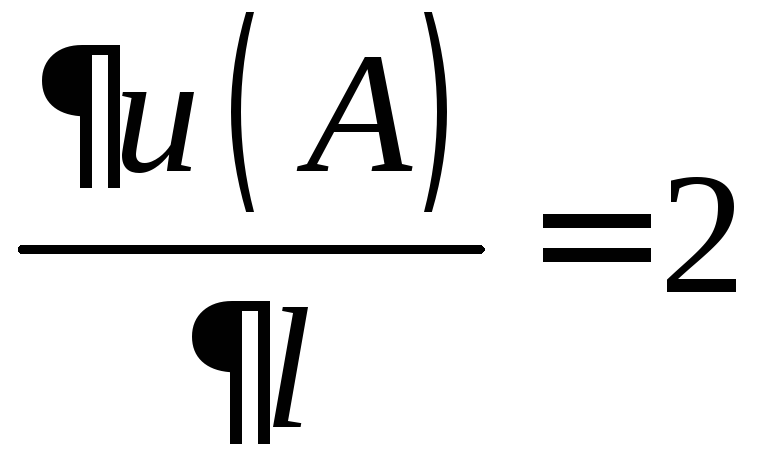 .
.![]()
Наибольшая
скорость возрастания скалярного поля
в точке
![]() равна 2.
равна 2.
