
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
1.2 Производные и дифференциалы
Рассмотрим
функцию
![]() ,если
изменяется только один из аргументов.
,если
изменяется только один из аргументов.
ОПРЕДЕЛЕНИЕ.
Частной
производной функции
![]() по
аргументу
по
аргументу
![]() в точке
в точке![]() называют предел
называют предел
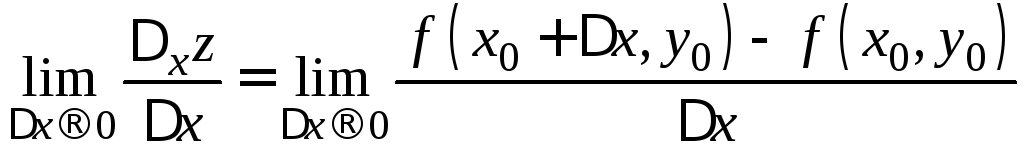
и
обозначают одним из символов: 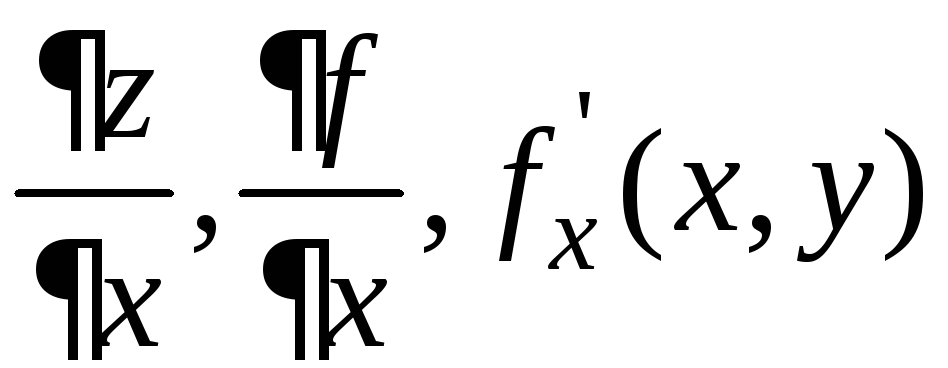 .
.
Аналогично
определяется частная
производная
![]() по аргументу
по аргументу![]() :
:
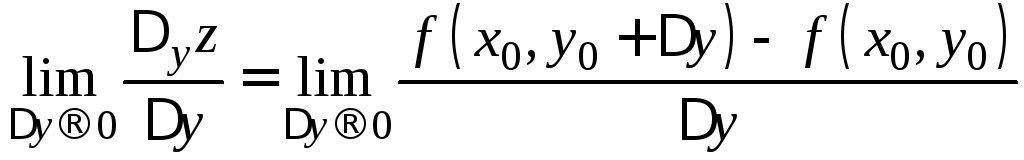 .
.
По
определению, каждая частная производная
является фактически производной функции
одной переменной:
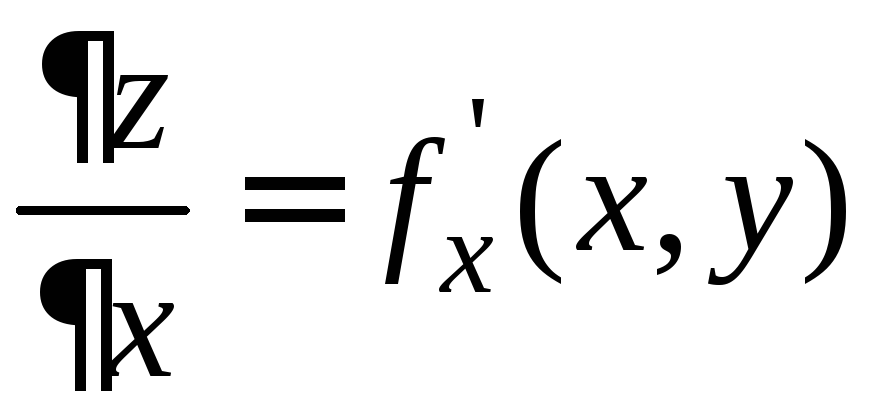 (гдеу = const),
(гдеу = const),
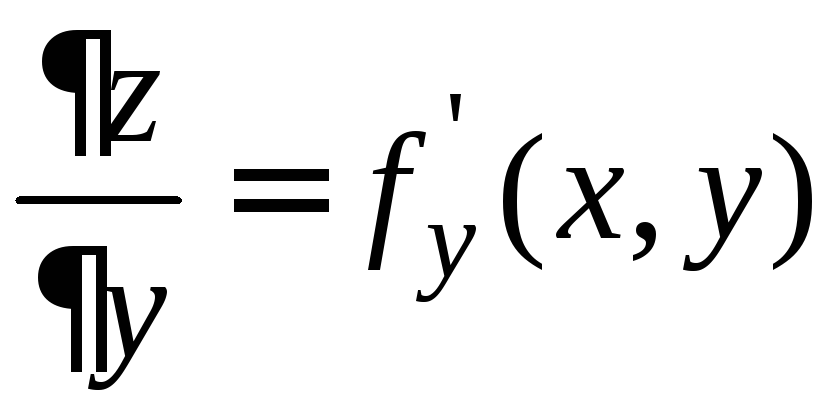 (где
(где
![]() =
const). Поэтому при вычислении частных
производных можно пользоваться уже
известными правилами и формулами
дифференцирования функции одной
переменной, считая при этом другую
переменную фиксированной.
=
const). Поэтому при вычислении частных
производных можно пользоваться уже
известными правилами и формулами
дифференцирования функции одной
переменной, считая при этом другую
переменную фиксированной.
Пример.
Найти частные производные функции
![]() .
.
РЕШЕНИЕ
Имеем
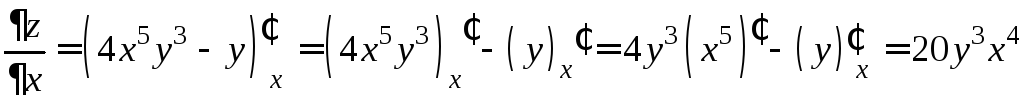
(![]() фиксировано);
фиксировано);
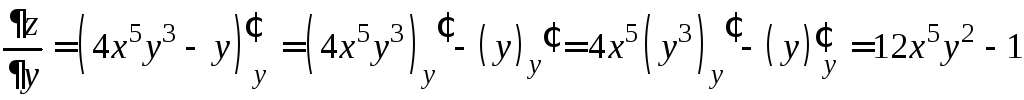
(![]() фиксировано).
фиксировано).
Пример.
Дано
![]() .
Найти
.
Найти![]() и
и![]() ,
вычислить их значения в точкеА(1;
2).
,
вычислить их значения в точкеА(1;
2).
РЕШЕНИЕ
Имеем
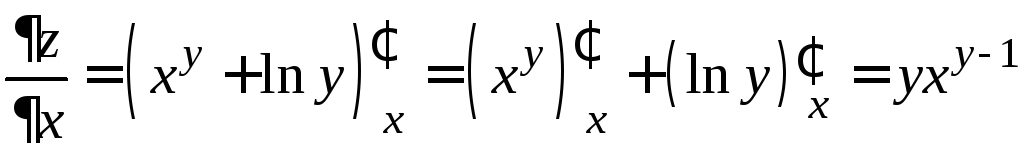
(при
фиксированном
![]() производная первого слагаемого находится
как производная степенной функции, а
второго - как производная постоянной);
производная первого слагаемого находится
как производная степенной функции, а
второго - как производная постоянной);
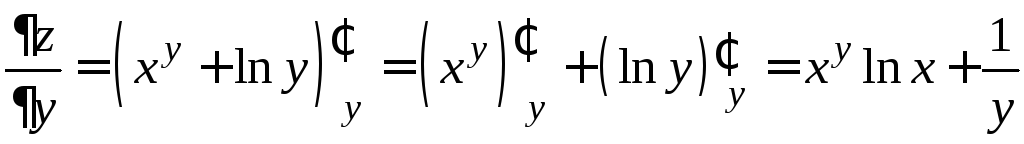
(при
фиксированном
![]() производная первого слагаемого находится
как производная показательной функции).
производная первого слагаемого находится
как производная показательной функции).
Вычислим значения частных производных в точке А(1; 2):
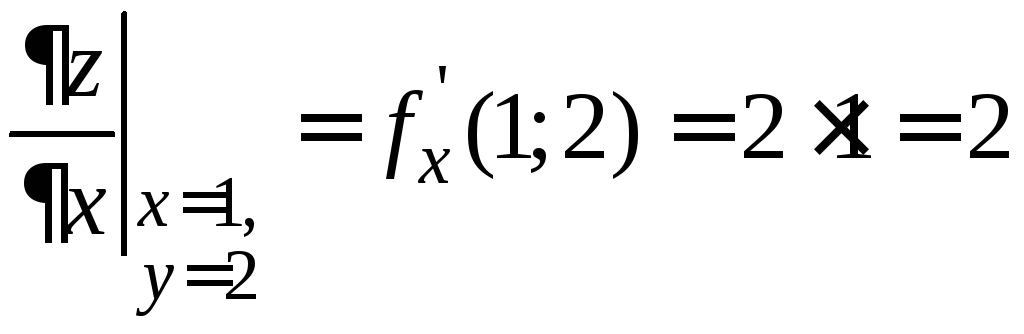 ;
; 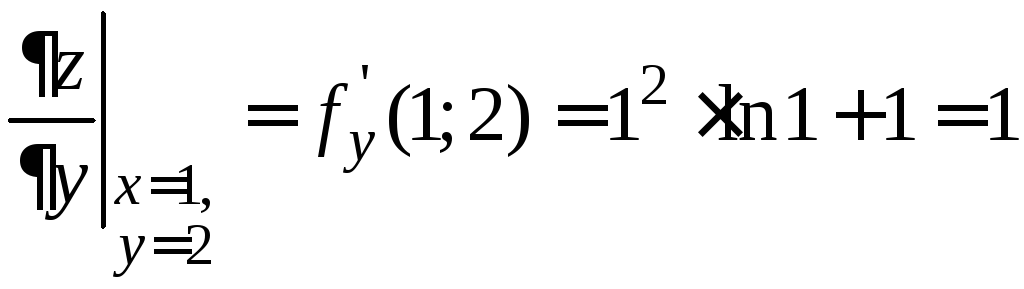 .
.
Аналогично определяются функции трех и более переменных. Если каждому набору значений (x; y; …; t) независимых переменных из множества D соответствует одно определенное значение u из множества E, то u называют функцией переменных x, y, …, t и обозначают u = f(x, y, …, t).
Для функции трех и более переменных геометрической интерпретации не существует.
Частные производные нескольких переменных определяются и вычисляются также в предположении, что меняется только одна из независимых переменных, а другие при этом фиксированы.
Пример.
Найти частные производные функции
![]() .
.
РЕШЕНИЕ
Имеем
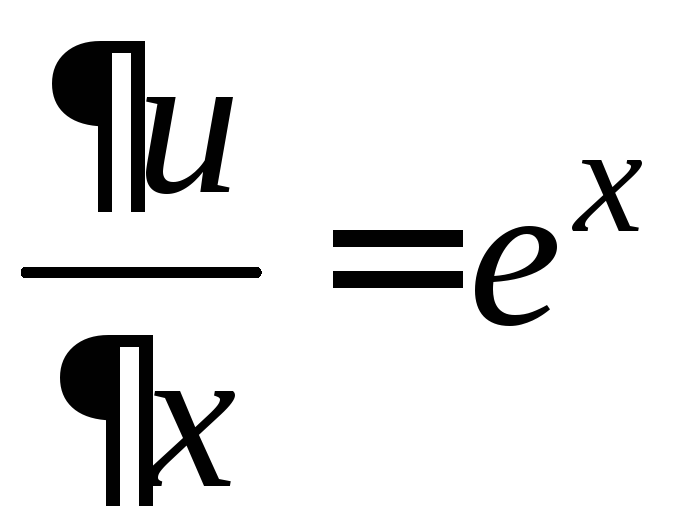 (у и
z
фиксированы);
(у и
z
фиксированы);
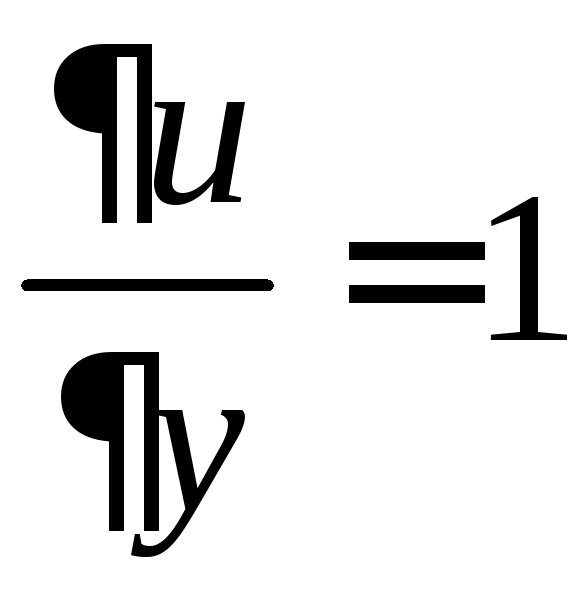 (
(![]() и
и
![]() фиксированы);
фиксированы);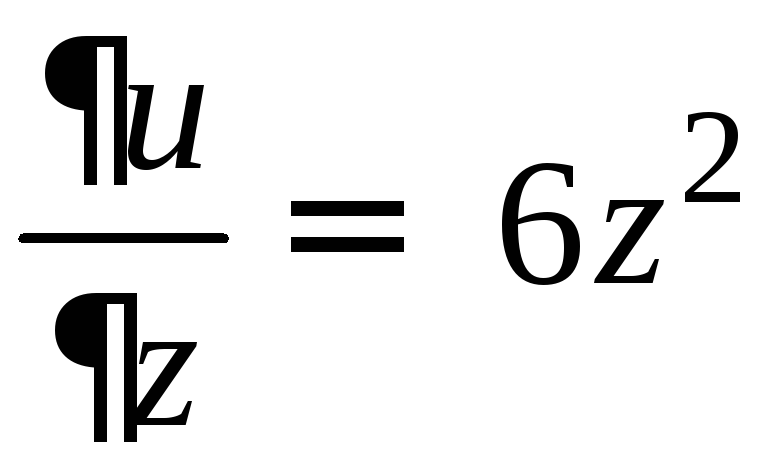 (
(![]() и y
фиксированы).
и y
фиксированы).
Частная производная функции нескольких переменных имеет тот же механический смысл, что и производная функции одной переменной - это скорость изменения функции относительно изменения одного из аргументов.
Пример. Количественная величина потока П пассажиров железных дорог может быть выражена функцией П = N2/R, где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстояние между пунктами.
Частная
производная функции П
по R,
равная
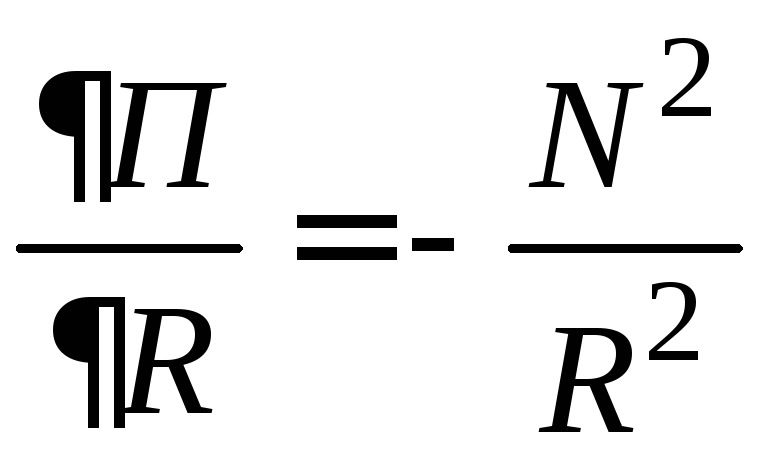 ,
показывает, что уменьшение потока
пассажиров обратно пропорционально
квадрату расстояния между корреспондирующими
пунктами при одной и той же численности
жителей в пунктах.
,
показывает, что уменьшение потока
пассажиров обратно пропорционально
квадрату расстояния между корреспондирующими
пунктами при одной и той же численности
жителей в пунктах.
Частная
производная функции П
по N,
равная
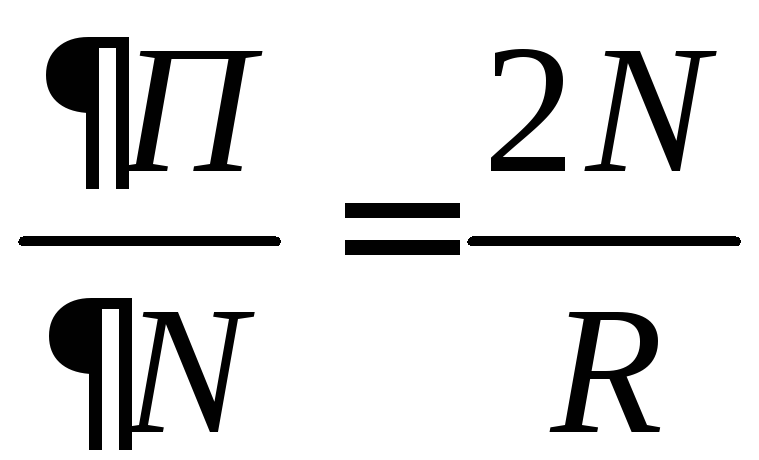 ,
показывает, что увеличение потока
пассажиров пропорционально удвоенному
числу жителей населенных пунктов при
одном и том же расстоянии между пунктами.
,
показывает, что увеличение потока
пассажиров пропорционально удвоенному
числу жителей населенных пунктов при
одном и том же расстоянии между пунктами.
ОПРЕДЕЛЕНИЕ. Полным
дифференциалом функции
![]() называют главную линейную часть полного
приращения функции, линейную относительно
приращений независимых переменных.
называют главную линейную часть полного
приращения функции, линейную относительно
приращений независимых переменных.
Обозначая
дифференциал буквой
![]() ,
можно записать
,
можно записать![]() ,
,![]() ,
,
где
![]() не зависят от
не зависят от![]() ,
,![]() - бесконечно малые при
- бесконечно малые при![]() .
.
Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемой в этой области.
Сформулируем без доказательства достаточное условие дифференцируемости функции.
ТЕОРЕМА.
Если
функция
![]() имеет непрерывные частные производные
имеет непрерывные частные производные![]() и
и![]() в данной области, то она дифференцируема
в этой области и ее дифференциал
выражается формулой
в данной области, то она дифференцируема
в этой области и ее дифференциал
выражается формулой

Произведение частной производной на приращение соответствующей независимой переменной называют частным дифференциалом. Частные дифференциалы обозначают:
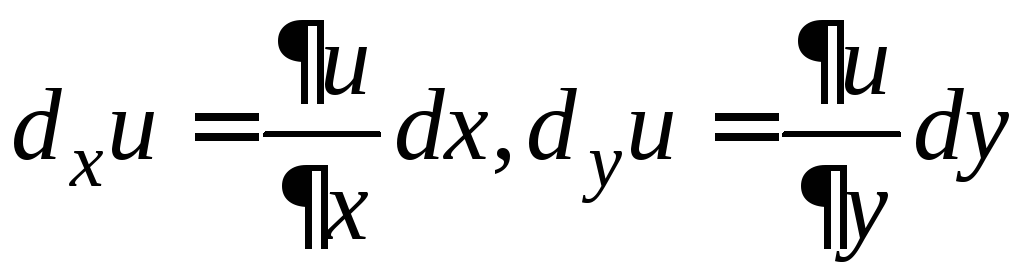 .
.
Сумма частных дифференциалов дает полный дифференциал.
Пример.
Найти полный
дифференциал функции
![]() .
.
РЕШЕНИЕ
Найдем частные производные функции и запишем полный дифференциал:
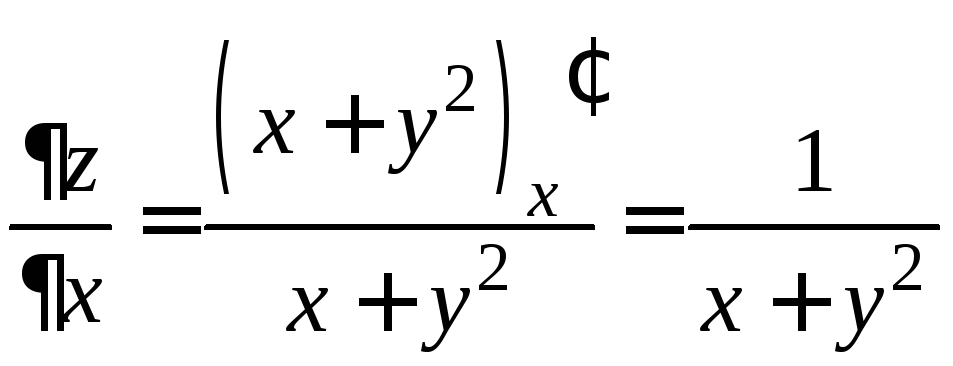 ,
, 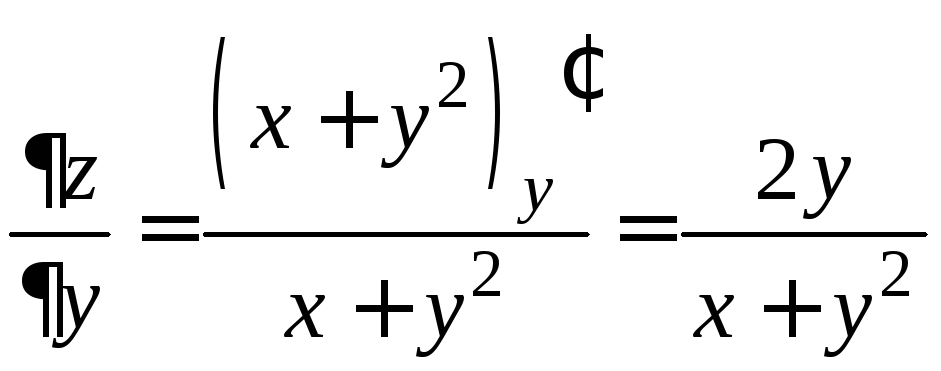 ,
,
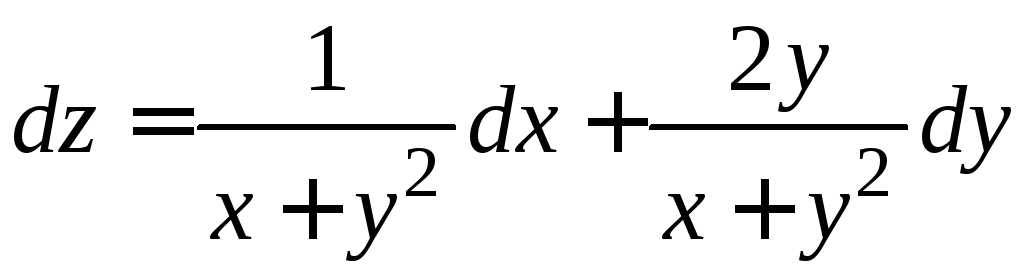 .
.
Так же как и в случае функции одной переменной, из дифференцируемости функции в некоторой области следует ее непрерывность в этой области, но не наоборот.
Частные
производные
![]() и
и![]() функции f(x,
y) сами
являются некоторыми функциями тех же
переменных и, в свою очередь, могут иметь
производные по разным переменным,
которые называют частными
производными высших порядков.
Каждая производная первого порядка
имеет две частные производные, которые
обозначают так:
функции f(x,
y) сами
являются некоторыми функциями тех же
переменных и, в свою очередь, могут иметь
производные по разным переменным,
которые называют частными
производными высших порядков.
Каждая производная первого порядка
имеет две частные производные, которые
обозначают так:
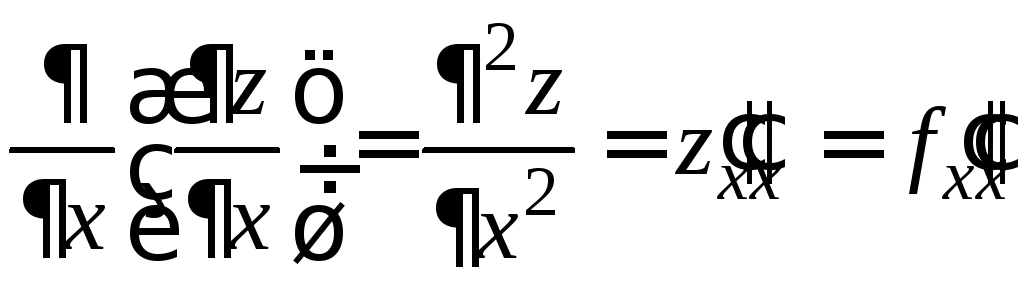 ,
,
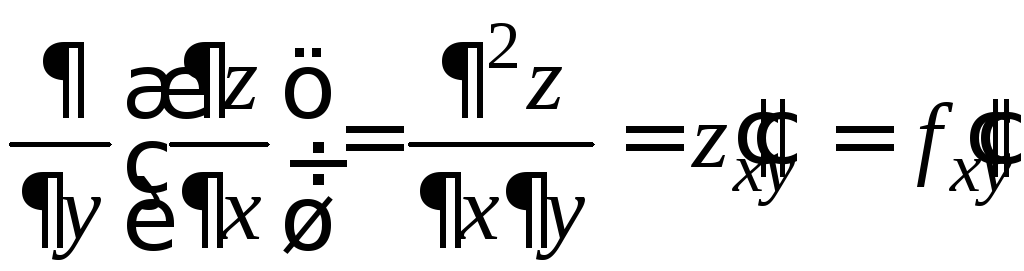 ,
,
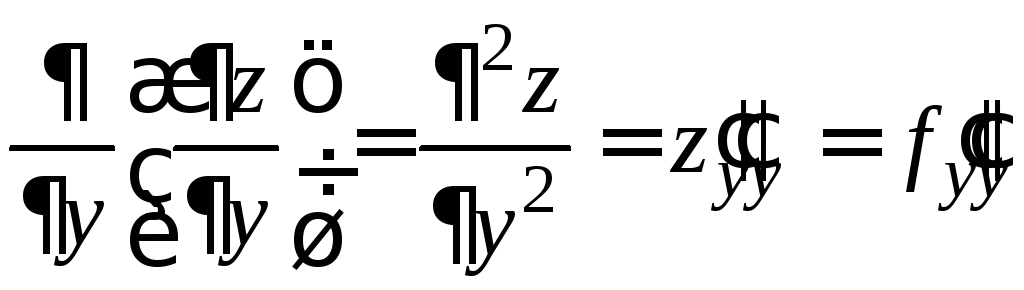 ,
,
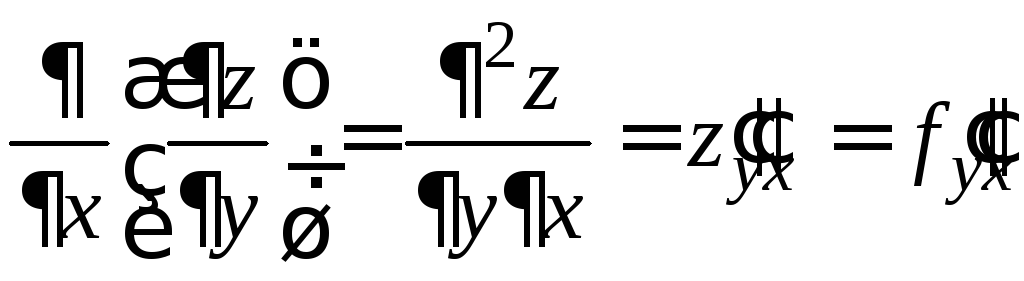 .
.
Производные
![]() называютсмешанными
производными.
называютсмешанными
производными.
Теорема.
Если
смешанные производные
![]() и
и![]() непрерывны в некоторой открытой области,
то они равны между собой.
непрерывны в некоторой открытой области,
то они равны между собой.
Другими словами, для непрерывной смешанной производной порядок дифференцирования не играет роли.
Пример.
Убедиться в равенстве смешанных
производных
![]() и
и![]() для функции
для функции![]() .
.
РЕШЕНИЕ
В
любой точке
![]() имеем
имеем

Как
и следовало ожидать,
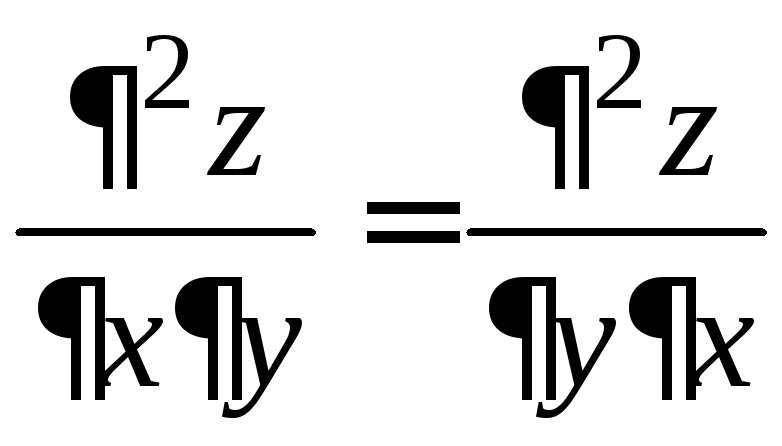 .
.
Частные производные от производных второго порядка называют частными производными третьего порядка и т. д.
Аналогично определяются частные производные высших порядков для функций любого числа независимых переменных.
