5.2 Числовые ряды с положительными членами

Числовой ряд 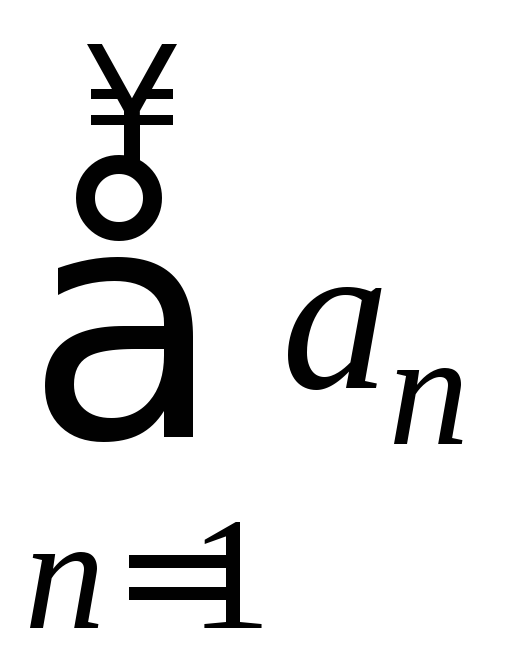называют рядом с положительными членами, если все его члены неотрицательны, т.е. если

Практически редко возникает необходимость в вычислении суммы ряда, а достаточно знать, сходится ряд или расходится. Установить это можно с помощью достаточных признаков сходимости.

Интегральный признак Коши

Пусть 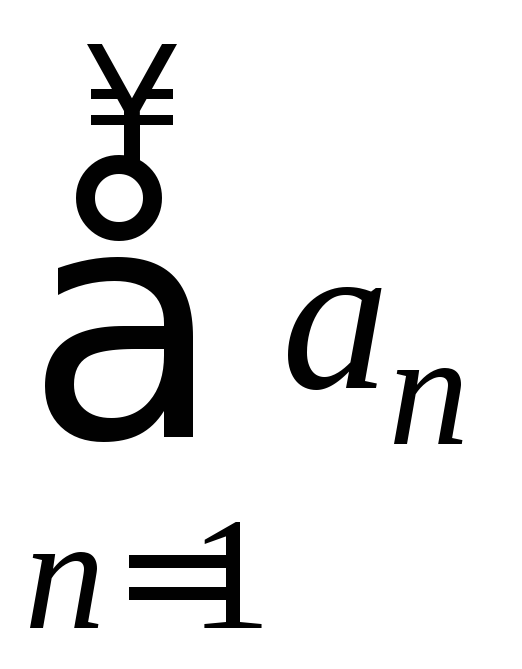- числовой ряд с положительными членами, и пусть- непрерывная, монотонно убывающая функция, для которой. Тогда ряд сходится, если сходится несобственный интеграл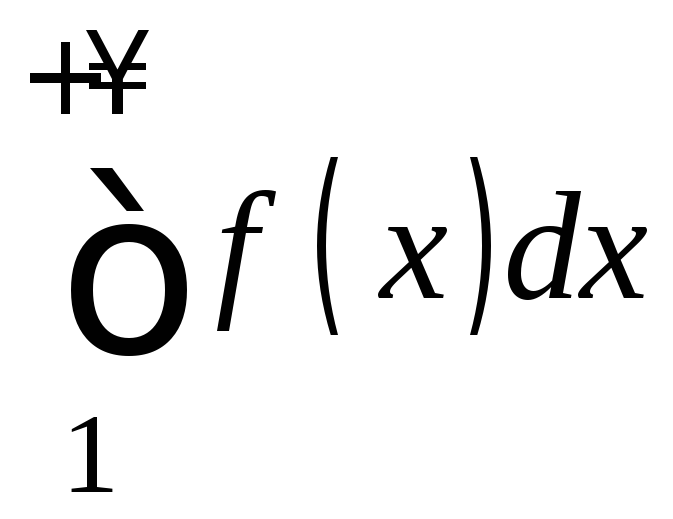, и расходится, если этот интеграл расходится.

ДОКАЗАТЕЛЬСТВО

Составим частичную сумму ряда . Поскольку(), то.

Каждое слагаемое частичной суммы можно рассматривать как площадь прямоугольника с основанием единица и высотой равной (рис.25). Добавление к частичной сумме нового члена ряда означает добавление новой площади, а потому, то есть последовательность частичных сумм неубывающая.

Рассмотрим частичную сумму и примем заплощадь прямоугольника, лежащего справа от, т. е. с большей высотой. Тогда получим сумму площадей прямоугольников, часть площади которых расположена над кривой. Эта сумма равна.

Р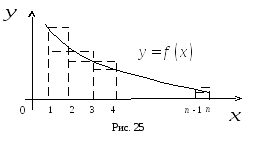ассмотрим также сумму. Каждое слагаемое этой суммы есть площадь треугольника с основанием, равным единице и высотой прямоугольника, лежащего слева. Тогда суммаесть сумма площадей прямоугольников, лежащих под кривой.

Обозначим 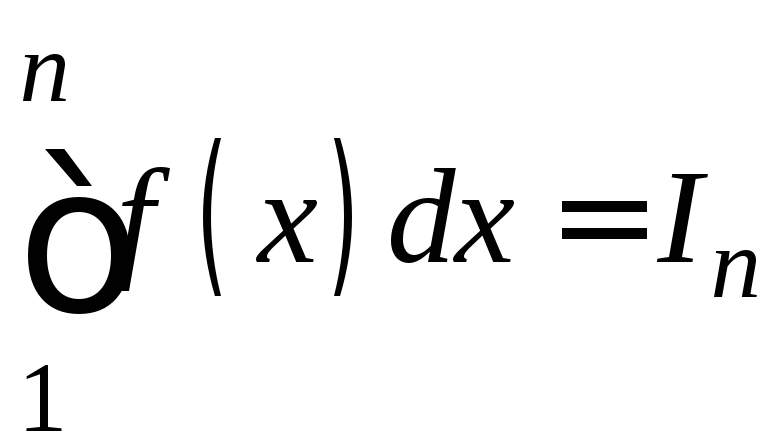. С геометрической точки зрения этот интеграл есть площадь, ограниченная кривойприи осью.

Тогда из рис. 25 имеем, что

.

Это двойное неравенство можно записать в виде двух неравенств:

и .

1). Пусть 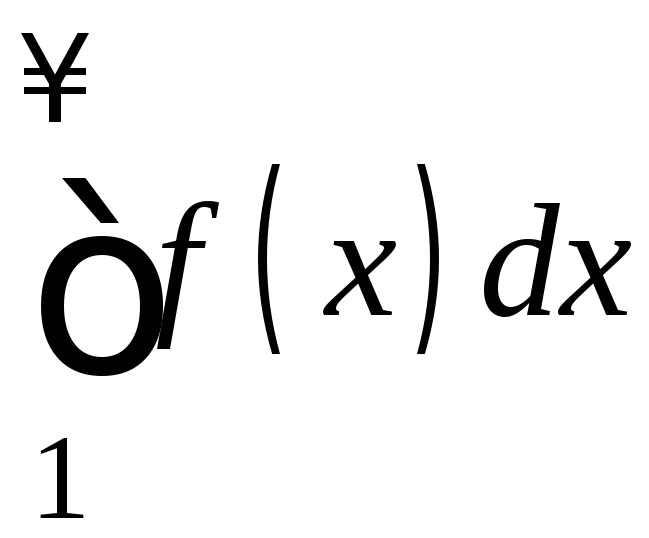сходится. Это значит, что существует конечный предел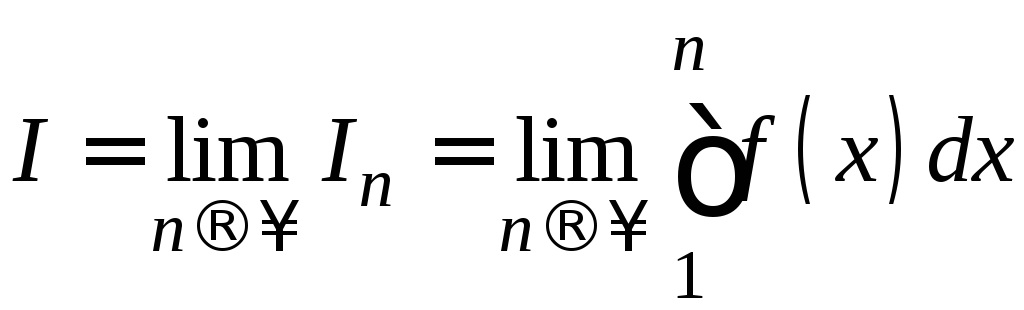. Тогда согласно первому неравенству, где- число. Следовательно, возрастающая последовательностьограниченна сверху, а потому имеет конечный предел, т. е. ряд сходится.

2). Пусть 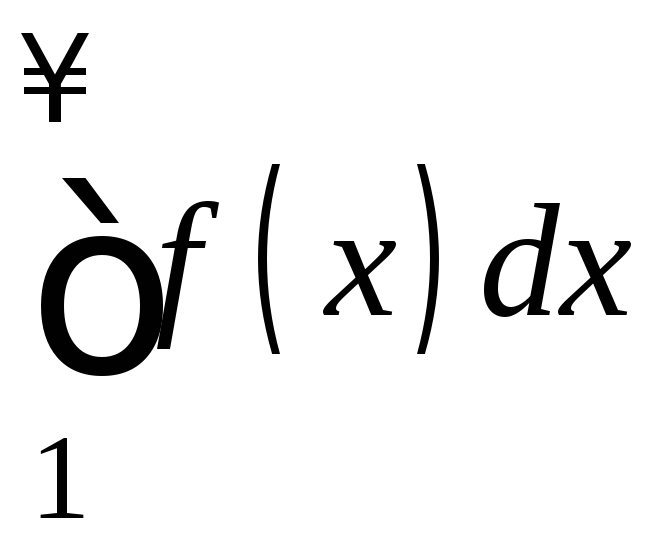расходится. Тогда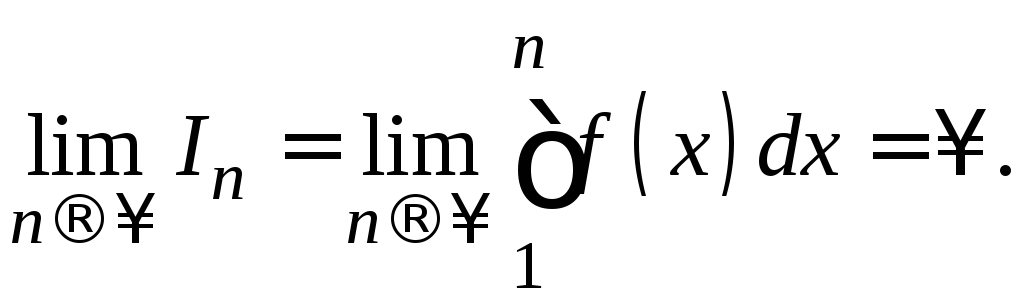

Согласно неравенству , частичные суммынеограниченно возрастают. Но тогда, по определению, ряд расходится.

ПРИМЕР. Исследовать на сходимость обобщенный гармонический ряд .

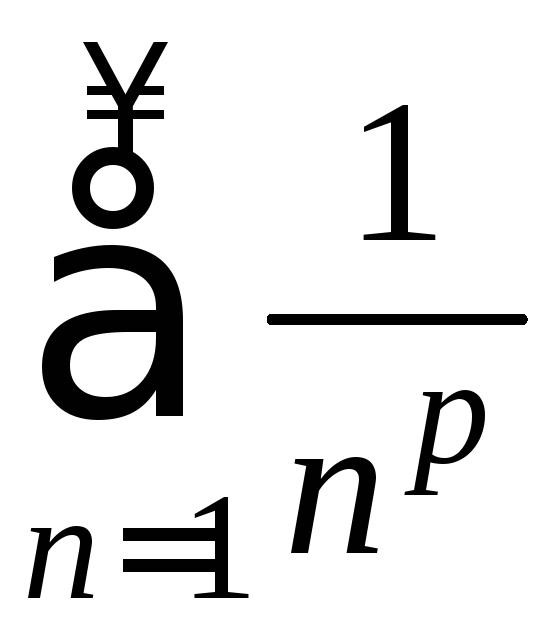РЕШЕНИЕ

Если , то члены ряда составляют монотонно убывающую последовательность.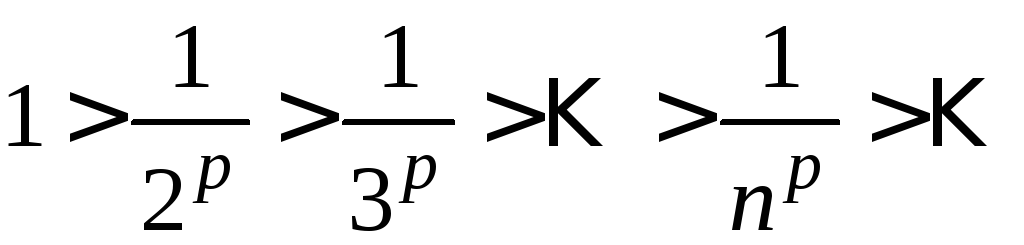

Рассмотрим функцию 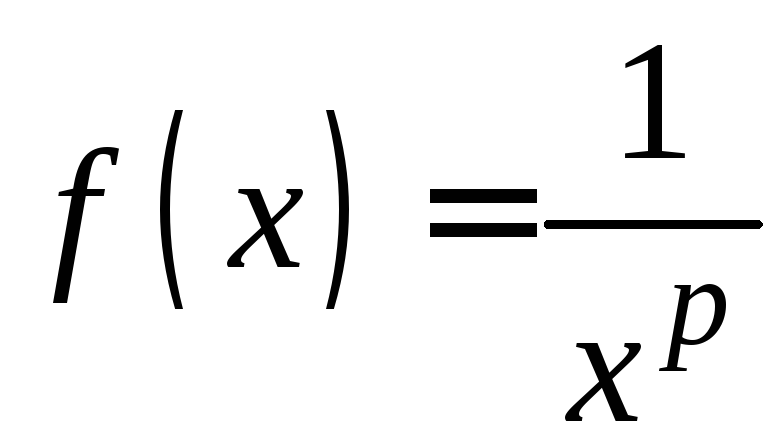непрерывную на промежутке, монотонно убывающую и при целых значениях аргумента, совпадающую с членами ряда.

Вычислим , если:

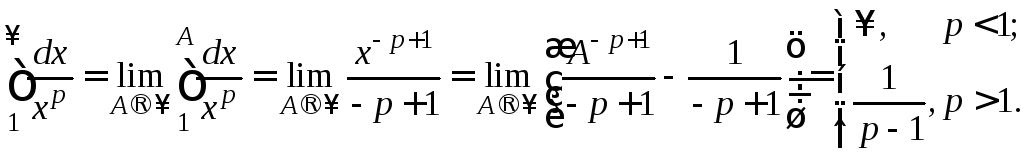
Если , то.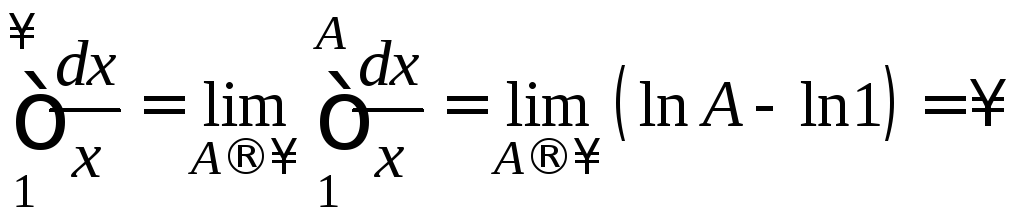

Таким образом, ряд 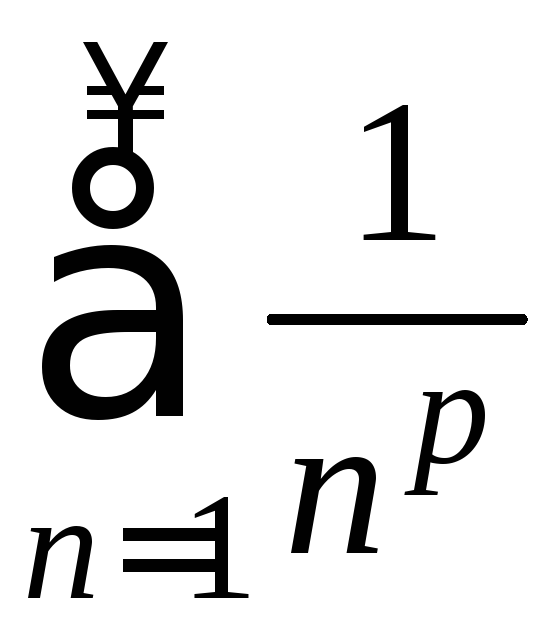сходится, еслии расходится если.

ПРИМЕР. Исследовать на сходимость ряд .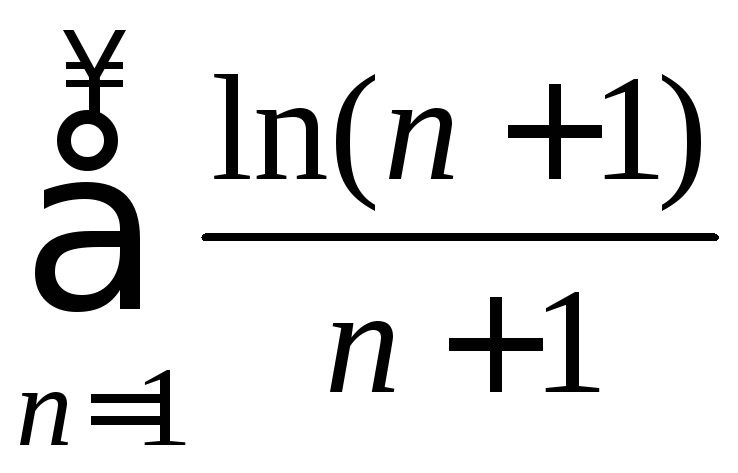

РЕШЕНИЕ

Общий член ряда 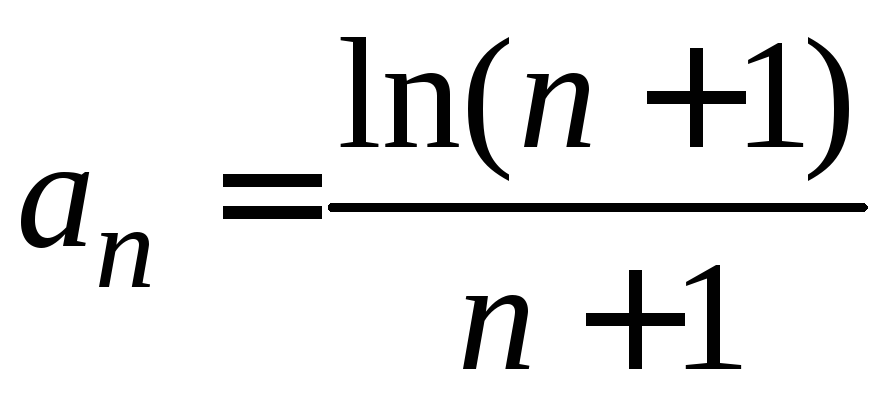. Вычислим интеграл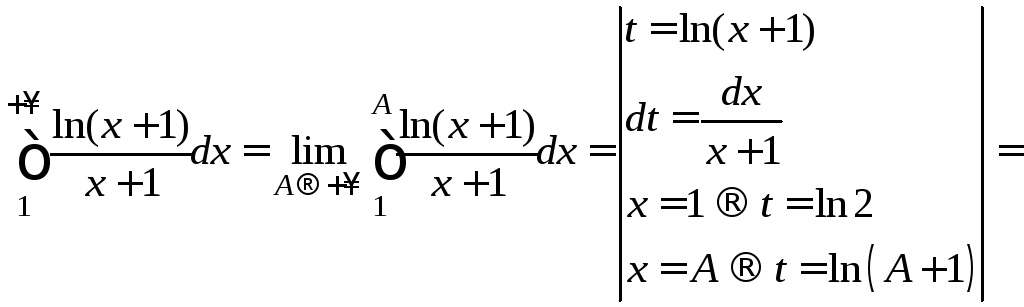

.

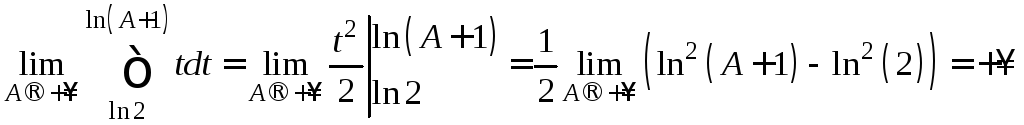Т.к. предел равен бесконечности, интеграл расходится. Следовательно, по интегральному признаку Коши, исследуемый ряд тоже расходится.

Рассмотрим два ряда с положительными членами:

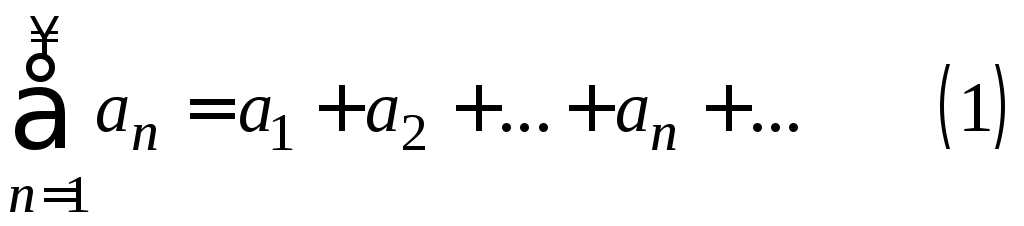
и

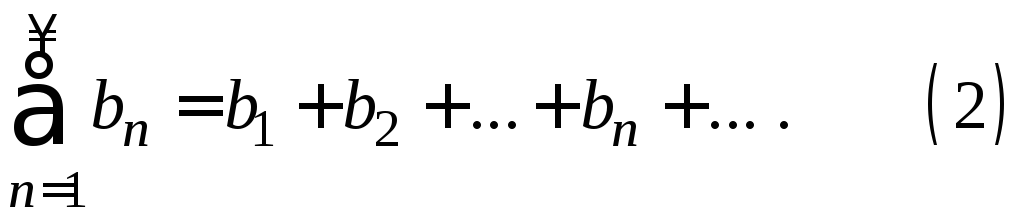
Первый признак сравнения

Если, начиная с некоторого номера, выполняется неравенство:, то из сходимости ряда (2) вытекает сходимость ряда (1), или из расходимости ряда (1) следует расходимость ряда (2).

ДОКАЗАТЕЛЬСТВО

На основании того, что отбрасывание конечного числа начальных членов ряда не изменяет его поведение, можно считать, что при всех значениях. Обозначим через- частичную сумму ряда (1), а через- частичную сумму ряда (2). Будем иметь:.

1). Пусть ряд сходится, тогда его частичные суммы ограничены суммой ряда. В силу предыдущего неравенства

.

Т.к. все члены ряда (1) неотрицательны, то последовательность его частичных сумм является монотонно возрастающей и ограниченной сверху . Известно, что такая последовательность имеет конечный предел. Это означает, что ряд (1) сходится.

2). Пусть ряд 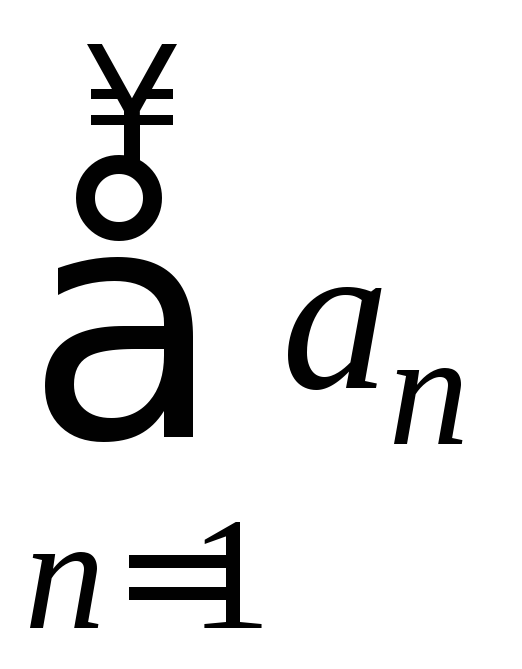расходится. Тогда его частичные суммы неограниченно возрастают, т.е.. Мы показали, чтопоэтому и. Ряд (2) также расходится.

Для решения примеров удобнее применять второй признак сравнения.