Несобственные интегралы с бесконечными пределами интегрирования
Пусть
функция
 определена и интегрируема на произвольном
обрезке
определена и интегрируема на произвольном
обрезке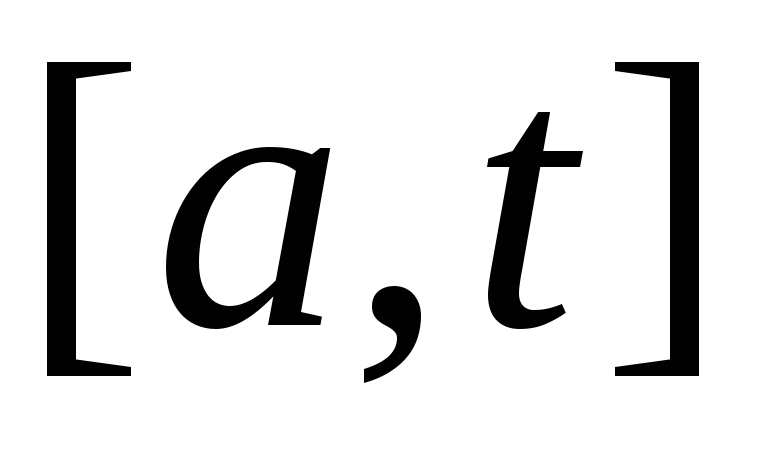 ,
т.е. функция
,
т.е. функция определена для произвольного
определена для произвольного .
.
Несобственным
интегралом с бесконечным верхним
пределом
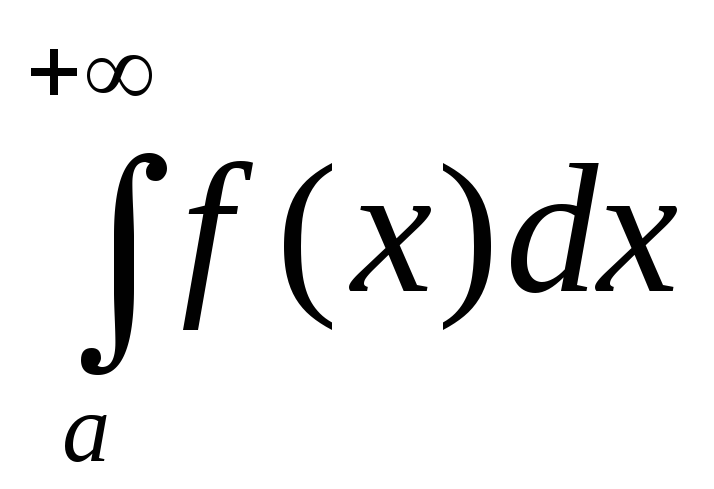 от непрерывной функции
от непрерывной функции на полуинтервале
на полуинтервале называется предел интеграла
называется предел интеграла при
при стремящемся к
стремящемся к ,
т.е.
,
т.е.
 .
.
Если
этот предел, стоящий в правой части
равенства, существует и конечен, то
несобственный интеграл называется
сходящимся
(к данному пределу), в противном случае
– расходящимся.
При
работе с несобственными интегралами
выделяют 2 задачи:
исследование
вопроса о сходимости заданного
несобственного интеграла;
вычисление
значения интеграла в случае, если
последний сходится.
Использование
несобственных интегралов позволяет
придать смысл такому понятию, как площадь
полубесконечной (бесконечной) фигуры.
Пример.
Вычислить
 .
.
Аналогично
определяется несобственный
интеграл от непрерывной функции с
бесконечным нижним пределом интегрирования,
а именно
 .
.
Несобственный
интеграл с двумя бесконечными пределами
интегрирования
имеет вид:
 ,
где
,
где .
.
Пример.
Вычислить
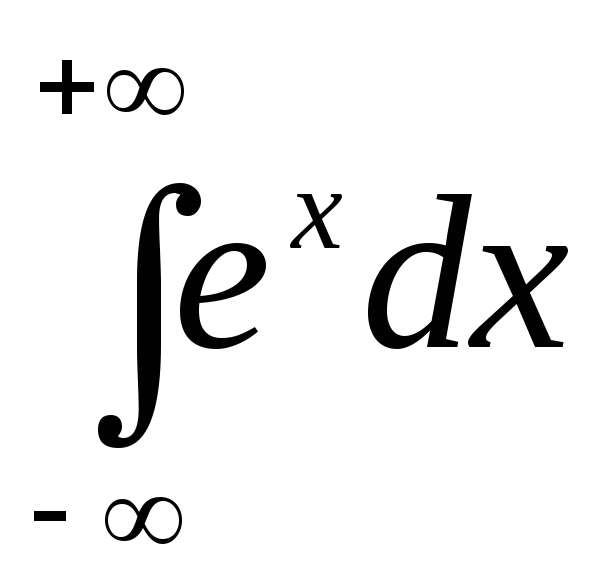 .
.
Задания для самостоятельной работы.
Найти
интегралы:
Найти
определенные интегралы:
Вычислить
площадь фигуры, ограниченную линиями:
 .
.
 .
.
 .
.
 .
.
Вычислить
интегралы или установить их расходимость:
13


