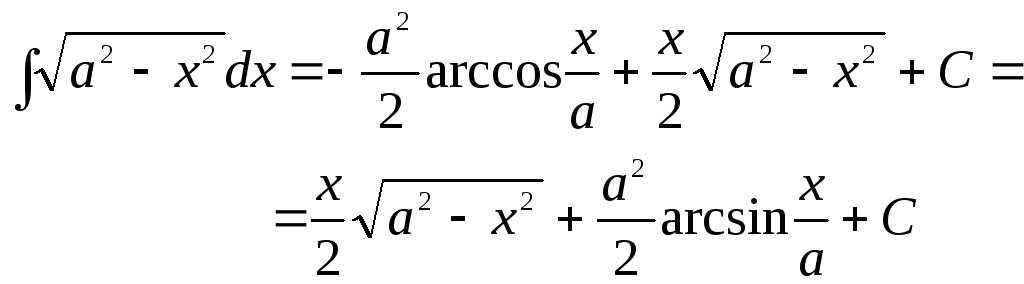Неопределенный и определенный интеграл Понятие первообразной и неопределенный интеграл

Функция называетсяпервообразной функцией для функции на промежутке, если в каждой точке этого промежутка.

Пример. А) является первообразной для, т.к.. Б)является первообразной для, т.к..

Если для функции существует первообразная, то она не является единственной. Например, функции,и вообще( некоторая произвольная постоянная) являются первообразными для функции . Таким образом можно сформулировать следующую теорему.

Теорема. Если и первообразные для функции на некотором промежутке, то найдется такое число, что будет справедливо равенство:.

Из данной теоремы следует, что, если  первообразная для функции, то выражение вида, где произвольное число, задает все возможные первообразные для .

Совокупность всех первообразных функции на промежуткеназываетсянеопределенным интегралом от функции и обозначается, где знак интеграла,  подынтегральная функция,  подынтегральное выражение,  некоторая первообразная для , произвольная постоянная.

Операция нахождения неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции. Данная операция является обратной для операции дифференцирования.

Правила интегрирования неопределенного интеграла:

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е. .

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. .

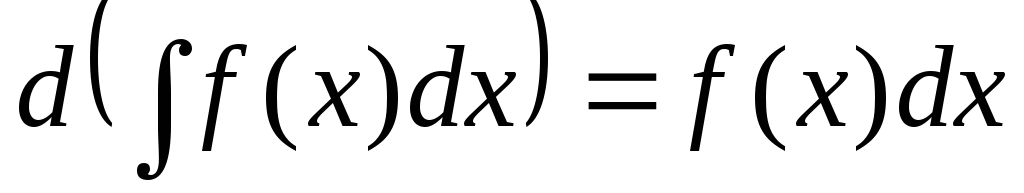3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .

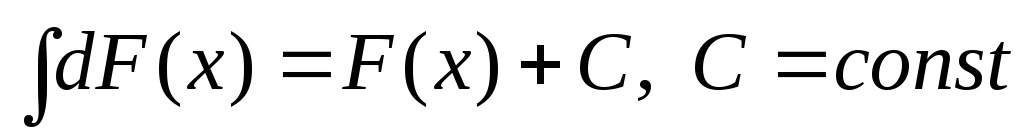4. Постоянный множитель можно выносить за знак интеграла, т.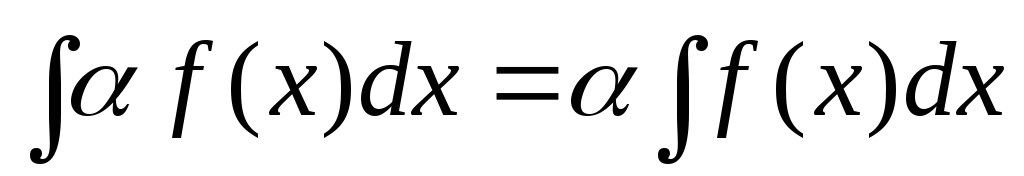е. , где некоторое число.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .

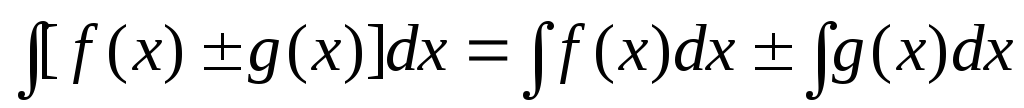Таблица простейших интегралов

Основные методы интегрирования неопределенного интеграла:

1. Непосредственное интегрирование. Вычисление интегралов с использованием основных правил и таблицы простейших интегралов.

Пример. Найти .

Пример. Найти .

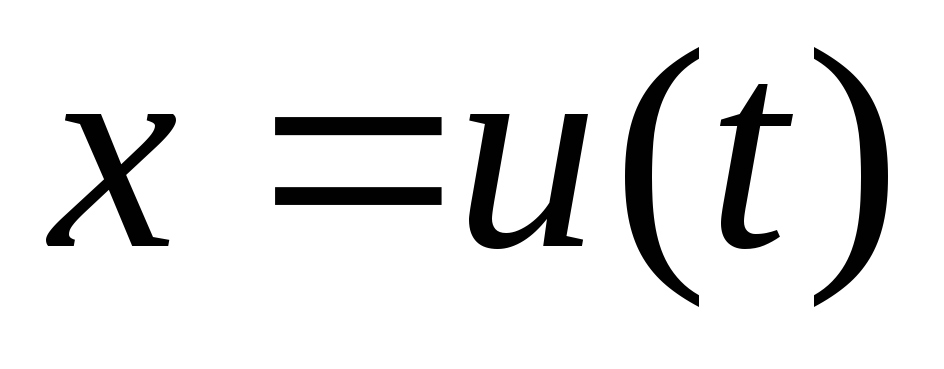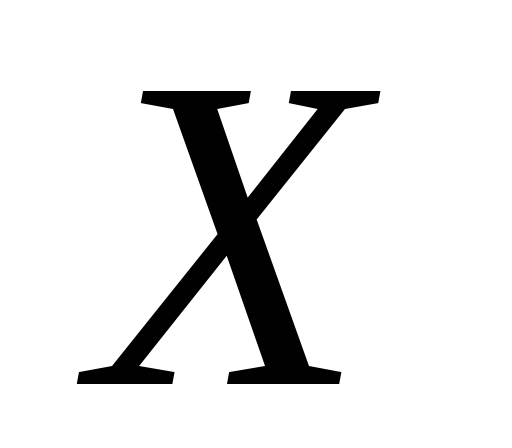
2. Метод замены переменной (метод подстановки). Данный метод основан на следующей теореме: Пусть функция определена и дифференцируема на отрезке , а  множество значений этой функции, на котором определена функция 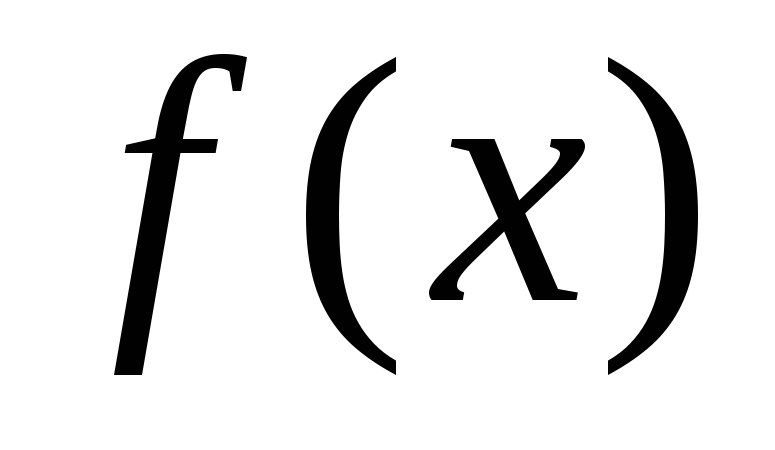. Тогда если , то получаем или .

Пусть заданный интеграл не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную: . Тогда , , т.е. .

Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, свести его к табличному.

Замечание. Новую переменную можно не выписывать явно, а производить преобразования функции под знаком дифференциала (путем введения постоянных и переменных под знак дифференциала).

Теорема. Пусть некоторая первообразная для функции . Тогда если вместо аргумента подынтегральной функции и первообразной подставить выражение , то это приведет к появлению дополнительного множителя перед первообразной: , где и  некоторые числа, .

Алгоритм метода:

1. Делаем замену.

2. Дифференцируем замену .

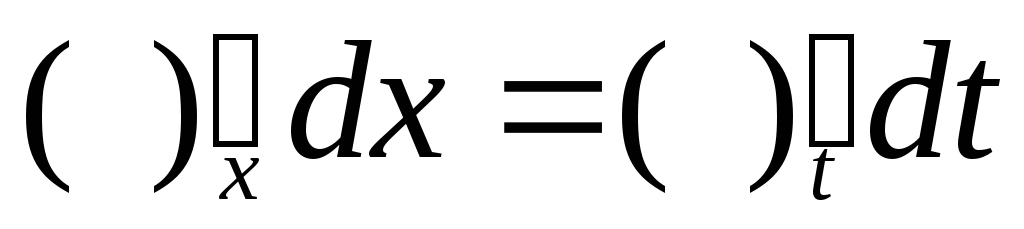3. Под знаком интеграла переходим к новой переменной.

4. Находим табличный интеграл.

5. Возвращаемся к старой переменной.

Пример. Найти .

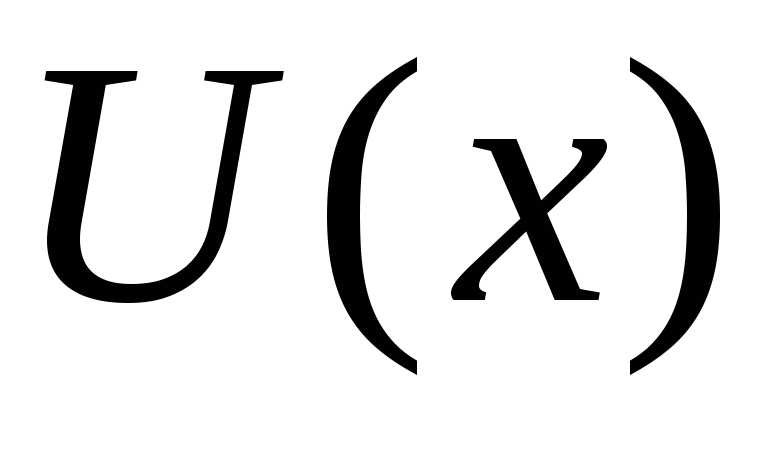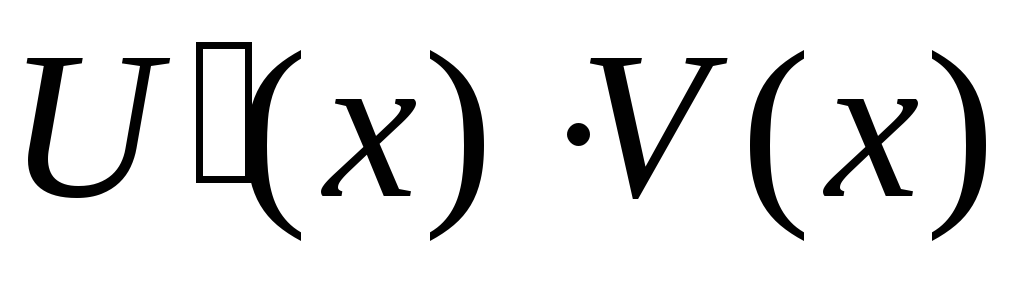3. Метод интегрирования по частям. Метод основан на теореме: Пусть функции и определены и дифференцируемы на промежутке , и функция имеет первообразную на этом промежутке. Тогда функция 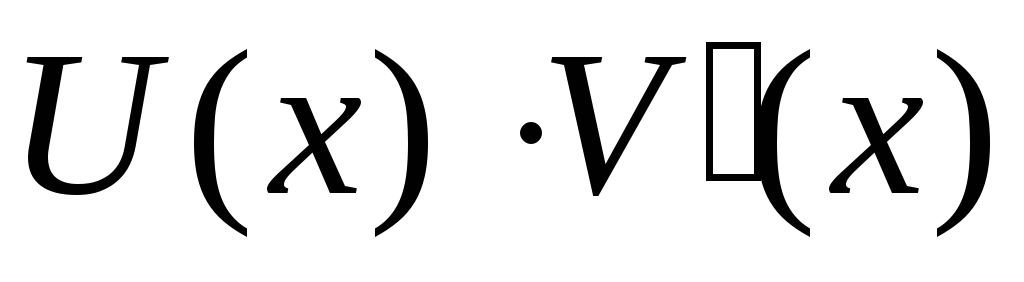также имеет первообразную на промежутке 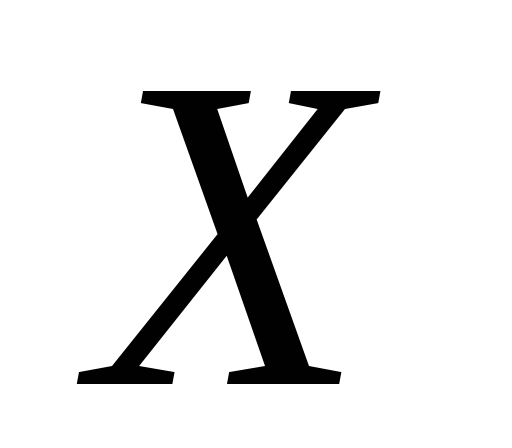, причем справедлива формула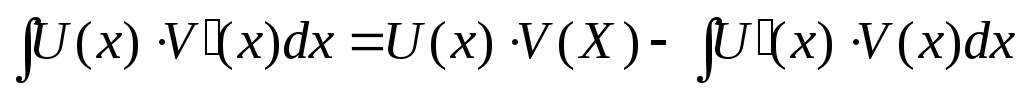. Учитывая, что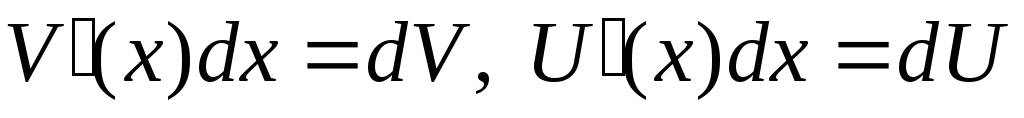, получим.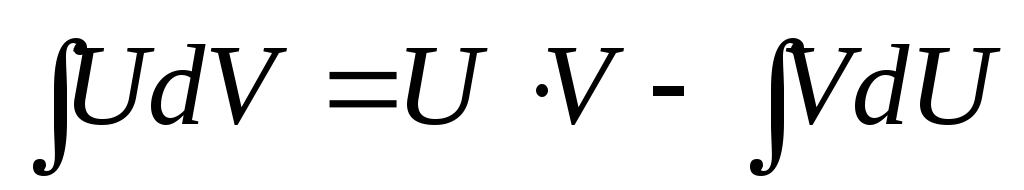

Интегрирование по частям состоит в том, что подынтегральное выражение представляется каким-либо образом в виде произведения двух множителей и (последний обязательно содержит ) и согласно формуле данное интегрирование заменяется двумя:

1) при отыскании из выражения для ;

2) при отыскании интеграла от .

Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.

Замечание. За нужно брать то, что после дифференцирования упрощается.

Пример. Найти .

Пример. Найти .