4. Тензорная функция и тензорная поверхность

Пусть в системе координат задан тензор второго ранга

Т

Тензорной функциейназывается функция

.

Поверхность

называется тензорной поверхностью.

Если привести тензор Tк главным осям, то

T´ ,

.

В этом случае при квадратичная формаи тензорная поверхность принимают каноническую форму:

,

.

Тензорная поверхность представляет собой:

1. При – эллипсоид (– сфера).

2. При ,– однополостный гиперболоид.

3. При ,– двуполостный гиперболоид.

4. При – мнимый эллипсоид.

Главные оси тензорной поверхности совпадают с главными осями тензора.

Для тензора первого ранга (вектора) тензорная функция имеет вид:

,

а тензорная поверхность:

,

то есть тензорная поверхность представляет собой плоскость, перпендикулярную вектору .

5. Оператор Гамильтона и его применение к скалярным, векторным и тензорным величинам

Оператором Гамильтонаили оператором(«набла») называется оператор

.

Символ обозначает производную по-ой координате. Набла () с греческого переводится как арфа.

Пусть – скалярная функция. Результатом применения оператора Гамильтона к скалярной функции является вектор

.

Заметим, что производная по направлению скалярного поляравна проекции градиента поля на это направление:

.

Пусть – векторная функция. Результатом применения оператора Гамильтона к векторной функции является тензор 2-го ранга

,

который называется векторным градиентомполя.

Покажем, что – тензор 2-го ранга.

Следовательно, по определению– тензор 2-го ранга.

Так же, как для скалярного поля, производная по направлению векторного поляравна проекции векторного градиента поля на это направление

.

Результатом применения оператора Гамильтона к тензору 2-го ранга является тензор 3-го ранга

.

Таким образом, применение оператора повышает ранг тензора на единицу.

С помощью символа (но не оператора!) можно также записать выражение для дивергенции и вихря (ротора) векторной функции:

,

.

Следует обратить внимание, что символом не всегда можно пользоваться как вектором. Например, смешанное произведение трех векторов есть скаляр

.

С другой стороны, выражение есть тензор третьего ранга.

Кроме того, для смешанного произведения векторов справедливо:

.

Однако, если один из векторов в этом равенстве заменить на оператор , то равенство перестанет быть верным:

.

Действительно,

,

.

Распишем более подробно операции и:

,

.

Продолжив вычисления, можно убедиться, что .

1. Тензор деформаций

1. Эйлеров и лагранжев тензоры деформаций

Рис.1.5.1

Деформация – это изменение взаимного расположения материальных частиц сплошной среды, которое вызывает изменение сил взаимодействия между материальными частицами.

Деформация малой окрестности некоторой точки определяется изменением длины и поворотом любого материального волокна (отрезка), исходящего из этой точки (Рис.1.5.1), то есть простейшими деформациями является относительное удлинение и сдвиг.

Для описания деформационного движения сплошной среды нужно определить изменение длины и поворот любого материального волокна. Пусть – пространственная декартова система координат с базисоми– материальные координаты частицы, равные ее пространственным координатам в начальный момент времени, то есть,– закон движения частицы.

Рис. 1.5.2

Материальным элементомс началом в частицеи соответствующим векторуназывается совокупность частиц, заполняющих бесконечно малый отрезок и имеющих лагранжевы координаты в пределах отдо(Рис. 1.5.2).

В текущий момент времени положение материального элемента определяется положениемего начальной точкии вектором

.

Для определения изменения длины составим выражение для квадратов длины материального элемента в начальныйив текущиймоменты времени:

,

.

Найдем изменение квадрата длины в лагранжевых переменных. Так как , то

,

.

Составим выражение для изменения квадрата длины материального элемента:

Выражение не зависит от конкретного материального элемента (волокна).

Тензор называетсялагранжевым тензором деформаций (тензором деформаций Грина).

Таким образом, изменение квадрата длины материального элемента выражается через лагранжев тензор деформаций:

.

Теперь выразим изменение квадрата длины материального элемента в эйлеровых переменных. В этом случае ,

,

,,

.

Тензор 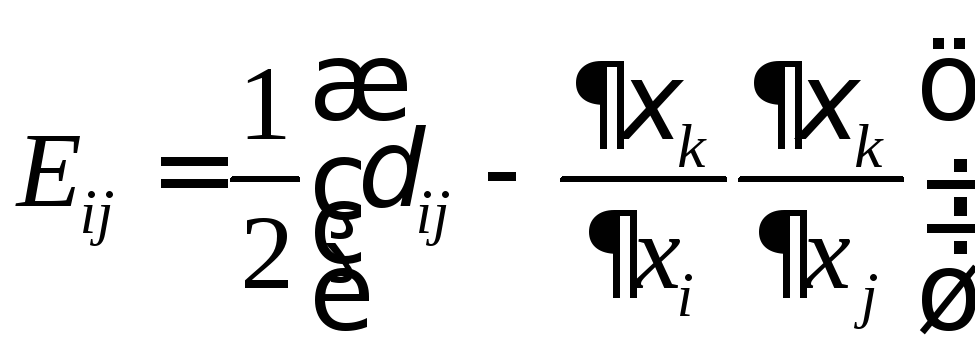называетсяэйлеровым тензором деформаций(тензором деформаций Альманси).

Изменение квадрата длины материального элемента выражается через эйлеров тензор деформаций:

.

Итак,

, ,

.

Легко видеть, что тензоры деформаций являются симметричными тензорами 2-го ранга.

Получим формулы для вычисления тензоров LиEчерез перемещение материальной частицы(Рис.1.5.3).

Рис.1.5.3

1. Лагранжево описание: ,.

Для вычисления лагранжева тензора конечных деформаций необходимы производные . Выразим эти производные через производные перемещения:

.

Подставим их в выражение для тензора:

.

Окончательно получаем:

2. Эйлерово описание: ,.

Аналогично, если выразить производные через производные перемещения, эйлеров тензор конечных деформаций примет вид:

.