3. Соотношения на разрыве в системе координат, связанной с покоящимся газом

Пусть перед ударной волной газ покоится, а волна бежит по нему со скоростью . Получим условия на ударной волне в неподвижной системе координат, связанной с покоящимся газом. Обозначим через– нормальную к поверхности скачка скорость газа за скачком, тогда скорости в подвижной и неподвижной системе координат связаны соотношением

или

, .

Подставим в , получим

.

В силу баланса массы

.

Поэтому баланс импульса примет вид

.

Таким образом, условия на ударной волне в неподвижной системе координат, когда газ перед волной покоится, имеют вид

.

4. Адиабата. Ударная адиабата

Адиабатойназывается линия на термодинамическойдиаграмме состояния, изображающая равновесный адиабатический процесс. В таких процессах отсутствует внешний теплообмен и энтропия сохраняется постоянной.

Уравнение адиабаты для совершенного газа имеет вид

или,

где .

Ему соответствует кривая, называемая адиабатой Пуассона (Рис. 3.4.3).

Рис. 3.4.3

Уравнение легко получить, используя термическое уравнение состояния (уравнение Клапейрона-Менделеева ), выражение для внутренней энергии ,

определение показателя адиабаты , соотношение Майера, условие отсутствия теплообмена(постоянства энтропии) и первое начало термодинамики

,

где – удельная внутренняя энергия,– газовая постоянная,,– удельные изобарная и изохорная теплоемкости,– количество теплоты, подводимое к системе,– удельный объем.

Отметим, что в адиабатическом процессе при переходе из начального состояния А в конечное Bсистема последовательно проходит все промежуточные состояния, определяемые уравнением адиабаты (Рис. 3.4.3).

Теперь получим уравнение ударной адиабаты для совершенного газа. Используя выражение для энтальпии

,

термическое уравнение состояния и определение показателя адиабаты, найдем, что

.

Для ударно-волнового процесса на диаграмме можно построить линию, исходящую из начального состояния газа перед ударной волной и состоящую из точек, соответствующих всевозможным состояниям газа за ударными волнами. По аналогии с адиабатой ее называют ударной адиабатой. Для вывода уравнения ударной адиабаты используем соотношения на разрыве в подвижной системе координат . Задача состоит в том, чтобы три уравнения свести к одному, исключив скорость и энтальпию. Для простоты опустим индексы, 2, относящиеся к значениям параметров за разрывом, а индекс 1 заменим на индекс 0. Третье уравнение перепишем, используя выражение энтальпии черези.

.

Из первого уравнения выразим

.

Тогда из второго уравнения с учетом можно выразить ичерези

,

.

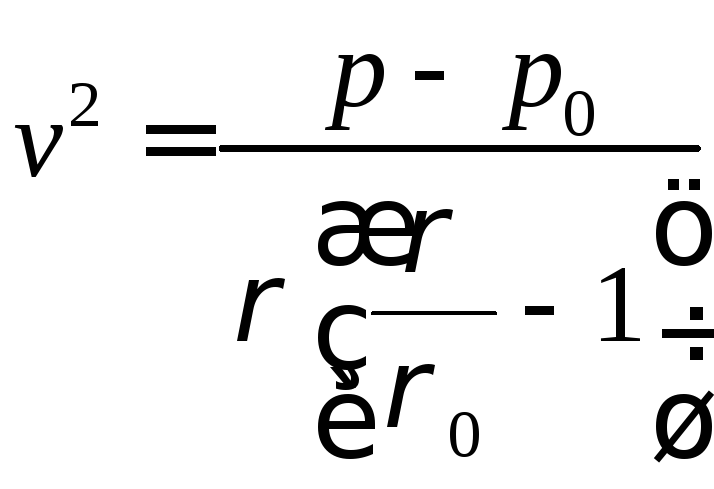Перейдем от к() и вычислим разность

Приравнивая правые части и , получим

.

Введем безразмерные параметры ,. Тогда

.

Выразив через, получим уравнениеударной адиабаты(адиабаты Гюгонио)

.

Его можно записать иначе, выразив через

.

В размерной форме уравнение ударной адиабаты имеет вид

,

.

Рассмотрим асимптотику параметров газа за скачком. При очень больших перепадах давления

:.

Следовательно, в ударной волне газ можно сжать только до определенного значения. Например, воздух () в ударной волне можно сжать не более чем в 6 раз.

Рис. 3.4.4. 1 – адиабата Пуассона, 2 – ударная адиабата (стрелкой показан переход из начального состояния в конечное)

В отличие от адиабаты Пуассона, ударная адиабата – это геометрическое место точек, соответствующих возможным состояниям газа за ударными волнами. Процесс изменения параметров газа при переходе через разрыв идет так, что из начального состояния газ мгновенно переходит в конечное состояние, не проходя последовательно промежуточные точки кривой (Рис. 3.4.4. 1 – адиабата Пуассона, 2 – ударная адиабата (стрелкой показан переход из начального состояния в конечное). В начальной точкекасательные к адиабатам Пуассона и Гюгонио совпадают, в чем легко убедиться непосредственным дифференцированием уравнений этих адиабат:

.

Поэтому для слабых волн вместо адиабаты Гюгонио можно использовать адиабату Пуассона.

Пусть за первой ударной волной идет вторая ударная волна. Чтобы построить ударную адиабату для второй волны, нужно за начальное состояние взять точку на первой ударной адиабате (линия 1 на Рис.3.4.5), соответствующую состоянию газа за первой волной. Поэтому вторая ударная адиабата (линия 2 на Рис. 3.4.5) не будет совпадать с ударной адиабатой для первой волны.

Рис. 3.4.5

Заметим, что энтропия газа за ударной волной больше, чем до нее, т.е. энтропия в ударной волне возрастает. Ударные волны могут использоваться для быстрой диссипации механической энергии.

Скачки разрежения в совершенном газе невозможны. Это утверждение (теорема Цемплена) доказывается в газовой динамике.