2. Всестороннее сжатие

Запишем выражение для давления при упругой деформации

.

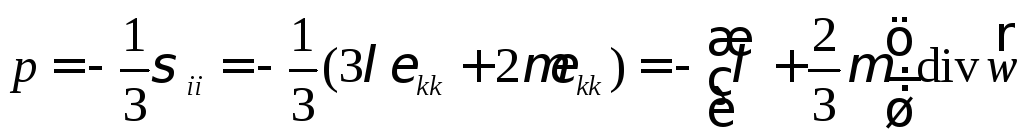Введем модуль объемной упругости

.

Тогда

.

Видим, что модуль объемной упругостихарактеризует сопротивление объемному сжатию.

Иногда используют обратную величину

– коэффициент сжимаемости.

Тогда

.

3. Сдвиг

Напряжение и деформация сдвига описываются недиагональными элементами тензоров деформаций и напряжений.

По закону Гука

,.

Это выражение напоминает закон течения ньютоновской жидкости, но вместо стоит.

Коэффициент называетсямодулем сдвигаи обозначается

.

В теории упругости пользуются парами коэффициентов упругости: , или, или. Эти коэффициенты выражаются друг через друга следующим образом

,,

,,

,,

,.

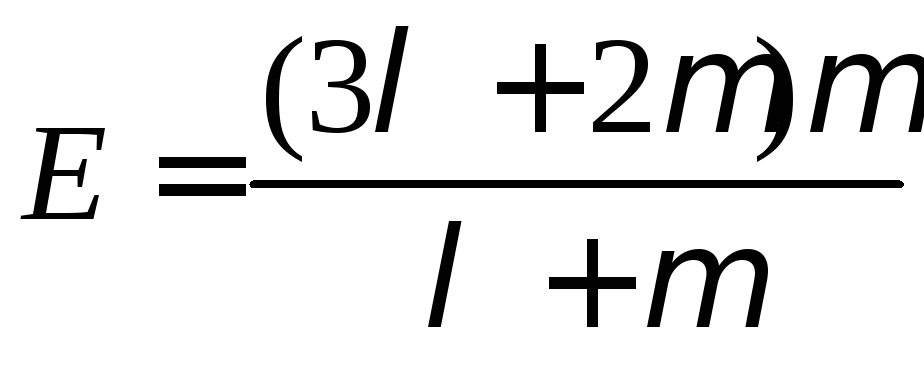Все модули неотрицательные, поэтому .

Видно, что при, поэтомусоответствует несжимаемому материалу.

Из закона Гука следует выражение для упругих деформаций через напряжения

.

1. Уравнения акустики

1. Уравнения акустики

Акустика изучает распространение звука или малых возмущений в сплошной среде. Уравнения акустики можно получить линеаризацией уравнений гидродинамики.

Как было показано выше, уравнения динамики идеальной жидкости имеют вид

Если считать течение баротропным, то есть

,

то система уравнений замкнута.

Пусть ,и. Здесь индексом 0 отмечены значения давления, плотности и скорости, усредненные по большому промежутку времени, и постоянные или начальные значения; а штрихом – возмущения этих величин. Предположим, что возмущениямалы по сравнению с. В рамках этого предположения получим уравнения для распространения малых возмущений, т.е. уравнения акустики. Будем сохранять лишь члены с возмущениями в первой степени. Тем самым линеаризуем уравнения гидродинамики. Разлагая в ряд Тейлора уравнение состояния , получим

,

или

.

По определению , гденазывается скоростью звука в среде. Тогда

.

Линеаризованное уравнение состояния называется акустическим уравнением состояния.

Предположим отсутствие поступательного движения, общего для всех точек сплошной среды, т.е. . Это предположение не ограничивает общности, так как можно перейти к системе координат, движущейся поступательно со скоростью, в которой жидкость будет покоиться.

Линеаризуем уравнение неразрывности

.

Линеаризуем уравнение импульсов

.

В отсутствие внешних массовых сил . Оставляя члены первого порядка, получим линеаризованное уравнение сохранения импульса

.

Выпишем замкнутую систему уравнений акустики- :

2. Волновое уравнение. Общее решение. Задача Коши и ее решение. Смешанная задача и ее решение

Перейдем в к безразмерным переменным:

Выпишем для одномерного случая систему уравнений акустики, опустив штрих и черту над безразмерными переменными:

После перекрестного дифференцирования, использованного ранее при решении уравнений несжимаемой жидкости, можно получить волновое уравнение для каждого из параметров,,:

.

Его общее решениеимеет вид

.

В этом можно убедиться, если сделать замену переменных:

Тогда получим

.

Очевидно, решение последнего имеет вид

.

Задача Коши для волнового уравнения. Поставим задачу Коши для волнового уравнения. Так как это уравнение второго порядка по времени, то необходимо для выделения искомого частного решения задать начальные условия дляи ее производной по времени. Таким образом, задача Коши имеет вид

Решение задачи Коши дает формула Даламбера

.

Смешанная задача. Если решение волнового уравнения ищется на отрезке, то необходимо задание граничных условий. Математическая постановка задачи формулируется следующим образом:

;

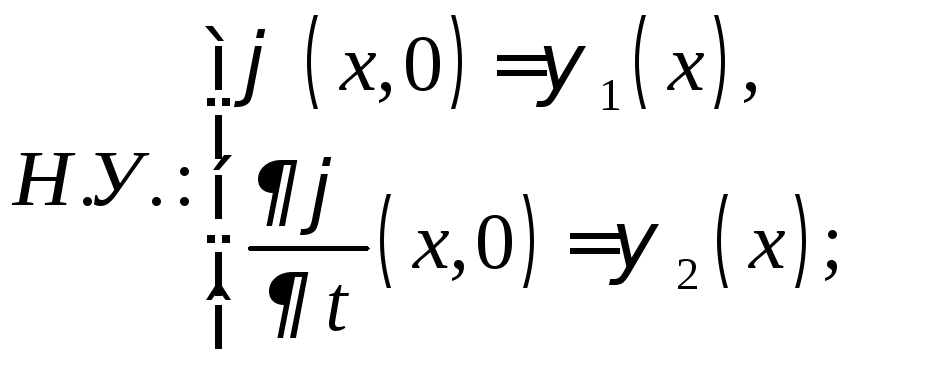
В частности, граничные условия могут быть заданы на полупрямой: , или.

Смешанная задача решается методами Фурье, преобразования Лапласа и другими. Когда аналитическое решение получить не удается, используют метод конечных разностей.