5. Методы построения математических функций

5.1. Общий вид

Методы, рассмотренные для правил и деревьев решений, работают наиболее естественно с категориальными переменными. Их можно адаптировать для работы с числовыми переменными, однако существуют методы, которые наиболее естественно работают с ними.

Рис. 5.5. Варианты линейного разделения обучающей выборки

Каждая из трех линий успешно разделяет все точки на два класса (представ­ленные на рисунке квадратами и кружками), однако модель должна быть представлена одной функцией, которая наилучшим образом решит задачу для новых объектов.

В результате задачу построения функции классификации и регрессии можно формально описать как задачу выбора функции с минимальной степенью представлена одной функцией, которая наилучшим образом решит задачу для новых объектов.

В результате задачу построения функции классификации и регрессии можно формально описать как задачу выбора функции с минимальной степенью ошибки:

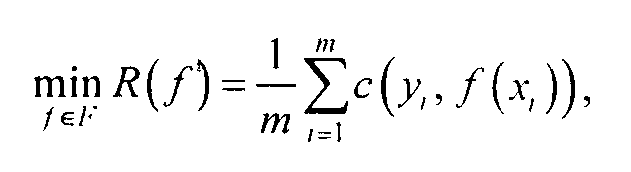(5.1).

где F— множество всех возможных функций; c(y,f(x,))— функция потерь (loss function), в которой f(x,) значение зависимой переменной, найденное с помощью функции f для вектора х,принадлежит Т, а у — ее точное (известное) значение.

Следует отметить, что функция потерь принимает неотрицательные значения. Это означает, что невозможно получить "вознаграждение" за очень хорошее предсказание. Если выбранная функция потерь все же принимает отрицательные значения, то это легко исправить, вводя положительный сдвиг (возможно, с зависимостью от x). Такими же простыми средствами можно добиться нулевых потерь при абсолютно точном предсказании f(x)= y. Преимущества подобного ограничения функции потерь заключаются в том, что всегда известен минимум и известно, что он достижим (по крайней мере, для данной пары х, у).

Для задач классификации и регрессии такие функции имеют разный вид. Так, в случае бинарной классификации (принадлежности объекта к одному из двух классов; далее первый класс обозначается через+1, а второй класс через-1) простейшая функция потерь (называемая "0-1 loss" в англоязычной литературе) принимает значение 1 в случае неправильного предсказания и 0 в противном случае:

Здесь не учитывается ни тип ошибки f(х) =1 (у = -1 — положительная ошибка, f(х) =-1, у = 1 — отрицательная ошибка), ни ее величина.

Небольшое изменение позволяет учесть характер ошибки:

Здесь c'(x,y,fix)) может учитывать многие параметры классифицируемого объекта и характер ошибки.

Cитуация усложняется в случае классификации с числом классов более двух. Каждый тип ошибки классификации в общем случае вносит свой тип потерь таким образом, что получается матрица размера k *к (где к— число классов).

При оценке величин, принимающих вещественные значения, целесообразно использовать разность fix) - у для оценки качества классификации. Эта разность в случае регрессии имеет вполне определенный смысл (например, размер финансовых потерь при неправильной оценке стоимости финансового инструмента на рынке ценных бумаг). Учитывая условие независимости от положения, функция потерь будет иметь вид

c(x,y,fix)) = c'(fix)-y).

Чаще всего применяется минимизация квадратов разностей fix)-у. Этот вариант соответствует наличию аддитивного нормально распределенного шума, влияющего на результаты наблюдений у_i.

Соответственно, минимизируем:

(5.2),