5.3.2. Метод Naive Bayes

Рассмотренный ранее lR-алгоритм формирует правила для принятия реше­ний лишь по одной переменной объекта. Однако это не всегда приемлемо. Нередко для классификации необходимо рассмотреть несколько независимых переменных. Такую классификацию позволяет выполнять алгоритм Naive Bayes, использующий формулу Байеса для расчета вероятности. Название naive (наивный) происходит от наивного предположения, что все рассматриваемые переменные независимы друг от друга. В действительности это не всегда так, но на практике все же данный алгоритм находит применение.

Вероятность того, что некоторый объект i_j, относится к классу с_r (т.е. у = с_r), обозначим как Р(у=с_r). Событие, соответствующее равенству независимых переменных определенным значениям, обозначим как Е, вероятность его наступления P(E). Идея алгоритма заключается в расчете условной вероятности принадлежности объекта к с_r при равенстве его независимых переменных определенным значениям.

При использовании формулы Байеса для оценки достоверности правила возникает проблема, связанная с тем, что в обучающей выборке может не быть ни одного объекта, имеющего значение c^h_d переменной х, и относящегося к классу с_г. В этом случае соответствующая вероятность будет равна 0, а следовательно, и вероятность такого правила равна 0. Чтобы избежать этого, к каждой вероятности добавляется некоторое значение, отличное от нуля. Такая методика называется оценочной функцией Лапласа.

Одним из действительных преимуществ данного метода является то, что пропущенные значения не создают никакой проблемы. При подсчете вероятности они просто пропускаются для всех правил, и это не влияет на соотношение вероятностей.

Числовые значения независимых переменных обычно обрабатываются с учетом того, что они имеют нормальное или Гауссово распределение вероятностей. Для них определяется математическое ожидание и среднеквадратичное отклонение.

В данном случае под математическим ожиданием понимается просто среднее число значений, т. е. сумма, разделенная на число объектов. Среднеквадратичное отклонение - это квадратный корень из типовой дисперсии.

4. Методы построения деревьев решений

4.1. Методика "разделяй и властвуй"

Общий принцип - подход к построению деревьев решений, основанный на методике "разделяй и властвуй", заключается в рекурсивном разбиении множества объектов из обучающей выборки на подмножества, содержащие объекты, относящиеся к одинаковым классам.

Относительно обучающей выборки Т и множества классов С возможны три ситуации:

• множество Т содержит один или более объектов, относящихся к одному классу с_г. Тогда дерево решений для Т - это лист, определяющий класс с_г;

• множество Т не содержит ни одного объекта (пустое множество). Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества, отличного от Т, например из множества, ассоциированного с родителем;

• множество Т содержит объекты, относящиеся к разным классам. В этом случае следует разбить множество Т на некоторые подмножества. Для этого выбирается одна из независимых переменных x_h, имеющая два и более отличных друг от друга значений с¹_h, c²_h,..., cⁿ_h ; T разбивается на подмножества Т_1,Т₂,..., Т_n, где каждое подмножество Т_i содержит все объекты, имеющие значение c'_h для выбранного признака. Эта процедура будет ре­курсивно продолжаться до тех пор, пока в конечном множестве не ока­жутся объекты только одного класса.

Очевидно, что при использовании данной методики построение дерева решений будет происходить сверху вниз. Описанная процедура лежит в основе, многих алгоритмов построения деревьев решений. Большинство из них являются "жадными алгоритмами". Это значит, что если один раз переменная была выбрана и по ней было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другую переменную, которая да­ла бы лучшее разбиение. Поэтому на этапе построения нельзя сказать, даст ли выбранная переменная в конечном итоге оптимальное разбиение.

При построении деревьев решений особое внимание уделяется выбору переменной, по которой будет выполняться разбиение. Для построения дерева на каждом внутреннем узле необходимо найти такое условие (проверку), которое бы разбивало множество, ассоциированное с этим узлом, на подмножества. В качестве такой проверки должна быть выбрана одна из независимых переменных. Общее правило для выбора можно сформулировать следующим образом: выбранная переменная должна разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т. е. количество объектов из других классов ("примесей") в каждом из этих множеств было минимальным. Разные алгоритмы реализуют различные способы выбора.

Другой проблемой при построении дерева является проблема остановки его разбиения. В дополнение к основному методу построения деревьев решений были предложены следующие правила:

• использование статистических методов для оценки целесообразности дальнейшего разбиения, так называемая ранняя остановка (prepruning). В конечном счете "ранняя остановка" процесса построения привлекательна в плане экономии времени обучения, но здесь уместно сделать одно важное предостережение: этот подход строит менее точные классификационные модели, и поэтому "ранняя остановка" крайне нежелательна. Признанные авторитеты в этой области Л. Брейман и Р. Куинлен советуют буквально следующее: "вместо остановки используйте отсечение";

• ограничить глубину дерева. Остановить дальнейшее построение, если разбиение ведет к дереву с глубиной, превышающей заданное значение;

• разбиение должно быть нетривиальным, т. е. получившиеся в результате узлы должны содержать не менее заданного количества объектов.

Этот список эвристических правил можно продолжить, но на сегодняшний день не существует такого, которое бы имело большую практическую ценность. К этому вопросу следует подходить осторожно, т. к. многие из правил применимы в каких-то частных случаях.

Очень часто алгоритмы построения деревьев решений дают сложные деревья, которые "переполнены данными", имеют много узлов и ветвей. В таких "ветвистых" деревьях очень трудно разобраться. К тому же, ветвистое дерево, имеющее много узлов, разбивает обучающее множество на все большее количество подмножеств, состоящих из все меньшего количества объектов. Ценность правила, справедливого, например, для 2-3 объектов, крайне низка, и в целях анализа данных такое правило практически непригодно. Гораздо предпочтительнее иметь дерево, состоящее из малого количества узлов, ко­торым бы соответствовало большое количество объектов из обучающей выборки. И тут возникает вопрос: а не построить ли все возможные варианты деревьев, соответствующие обучающему множеству, и из них выбрать дерево с наименьшей глубиной? К сожалению, Л. Хайфилем (L. Hyafill) и Р. Ривестом (R. Rivest) было показано, что данная задача является NP-полной, а, как известно, этот класс задач не имеет эффективных методов решения.

Для решения описанной проблемы часто применяется так называемое отсечение ветвей (pruning).

Пусть под точностью (распознавания) дерева решений понимается отношение правильно классифицированных объектов при обучении к общему количеству объектов из обучающего множества, а под ошибкой - количество неправильно классифицированных. Предположим, что известен способ оценки ошибки дерева, ветвей и листьев. Тогда можно использовать следующее простое правило:

• построить дерево;

• отсечь или заменить поддеревом те ветви, которые не приведут к возрастанию ошибки.

В отличие от процесса построения отсечение ветвей происходит снизу вверх, двигаясь с листьев дерева, отмечая узлы как листья либо заменяя их поддеревом. Хотя отсечение не является панацеей, но в большинстве практических задач дает хорошие результаты, что позволяет говорить о правомерности использования подобной методики.

Алгоритм ID3 - рассмотрим более подробно критерий выбора переменной, используемый в алгоритмах ID3 и С4.5. Очевидно, что полный набор вариантов разбиения описывается множеством |Х| (количеством независимых переменных).

Рассмотрим проверку переменной x_h, (в качестве проверки может быть выбрана любая переменная), которая принимает т значений c_h1, c_h2,…, c_hm. Тогда разбиение Т по проверке x_h, даст подмножества Т\, Т₂, ..., Т„„ при x_h равном соответственно с/,_ь с_/|2, ..., с_;„„. Единственная доступная информация — каким образом классы распределены в множестве Т и его подмножествах, получае­мых при разбиении. Именно она и используется при выборе переменной. В данном случае существует четыре варианта разбиения дерева (рис. 5.2).

Пусть freq(c_r, T) — количество объектов из множества /, относящихся к одно­му и тому же классу с,. Тогда вероятность того, что случайно выбранный объект из множества / будет принадлежать классу с/.

freq (c_r,l)

\т\ ■

Так для примера, рассмотренного в табл. 5.1, вероятность того, что в случай­но выбранный день игра состоится, равна 9/14.

Согласно теории информации оценку среднего количества информации, не­обходимого для определения класса объекта из множества Т, дает выражение:

Л

( гЛ

Т). Ьщ(с_г,Т)

log.

1^С" My

Info (Г) = -£ freq

Т

Поскольку используется логарифм с двоичным основанием, это выражение дает количественную оценку в битах. Для данного примера:

Info(7) = -9/14log₂(9/14) - 5/14-log₂(5/14) = 0,940 бит.

Ту же оценку, но только уже после разбиения множества Т по х/„ дает сле­дующее выражение:

inf_0jrt (г) = Х)т; /|r|info(7;).

Например, для переменной наблюдение оценка будет следующей:

1пК_аблюДение= (5/14)0,971 +(4/14)-0+(5/14)0,971 =0,693 бит.

Критерием для выбора атрибута будет являться следующая формула:

Gain(x/,) = Info(7) - Info.,/,(7).

Этот критерий считается для всех независимых переменных. В данном при­мере:

Сат(наблюдение) = 0,247 бит

Оаш(температура) = 0,029 бит

Оат(влажность) = 0,152 бит

Gain(BeTep)= 0,048 бит

Выбирается переменная с максимальным значением Gain(). Она и будет яв­ляться проверкой в текущем узле дерева, а затем по ней производится даль­нейшее построение дерева. То есть в узле будет проверяться значение по этой

ременной и дальнейшее движение по дереву будет производиться в зави­симости от полученного ответа. Таким образом, для случая с определением игры будет выбрана переменная наблюдение.

Такие же рассуждения можно применить к полученным подмножествам Г,, Тг, —, Т_т и продолжить рекурсивно процесс построения дерева до тех пор, пока в узле не окажутся объекты из одного класса.

Так для множества, полученного при значении солнечно переменной наблюдение, для остальных трех переменных будут следующие значения:

Gain(TeMnepaTypa) = 0,571 бит Оаш(влажность) = 0,971 бит

Gain(BeTep) = 0,020 бит

Таким образом, следующей переменной, по которой будет разбиваться под­множество Г_{солнечно}, окажется влажность. Построенное дерево будет выглядеть Г так, как изображено на рис. 5.3

Одно важное замечание: если в процессе работы алгоритма получен узел, ас­социированный с пустым множеством (ни один объект не попал в данный

узел), то он помечается как лист и в качестве решения листа выбирается наи­более часто встречающийся класс у непосредственного предка данного листа. Здесь следует пояснить, почему критерий Gain(X) должен максимизировать­ся. Из свойств энтропии известно, что максимально возможное значение эн­тропии достигается в том случае, когда все сообщения множества равноверо­ятны. В данном случае энтропия Info* достигает своего максимума, когда час­тота появления классов в множестве Т равновероятна. Необходимо выбрать такую переменную, чтобы при разбиении по ней один из классов имел наи­большую вероятность появления. Это возможно в том случае, когда энтропия Info* будет иметь минимальное значение и, соответственно, критерий Gain(JQ достигнет своего максимума.

Алгоритм С4.5 — рассмотренный способ выбора переменной использует алгоритм ID3. Однако он подвержен сверхчувствительности (overfitting), т. е. "предпочитает" переменные, которые имеют много значений. Например, если переменная уникально идентифицирует объекты, то ввиду уникальности каждого значения этой переменной при разбиении множества объектов по ней получаются подмножества, содержащие только по одному объекту. Так как все эти множества "однообъектные", то и объект относится, соответст­венно, к одному-единственному классу, поэтому

Значит критерий Gain(X) принимает свое максимальное значение, и, несом­ненно, именно эта переменная будет выбрана алгоритмом. Однако если рас­смотреть проблему под другим углом — с точки зрения предсказательных способностей построенной модели, то становится очевидным вся бесполез­ность такой модели.

В алгоритме С4.5 проблема решается введением некоторой нормализации. Пусть суть информации сообщения, относящегося к объекту, указывает не на класс, к которому объект принадлежит, а на выход. Тогда, по аналогии с оп­ределением Info(7), имеем:

Это выражение оценивает потенциальную информацию, получаемую при разбиении множества Т на т подмножеств.

Рассмотрим следующее выражение:

Пусть это выражение является критерием выбора переменной.

Очевидно, что переменная, идентифицирующая объект, не будет высоко оценена критерием gain ratio. Пусть имеется k классов, тогда числитель выражения максимально будет равен log2k:, и пусть п - количество объектов в обучающей выборке и одновременно количество значений переменных, тогда знаменатель максимально равен log₂ n. Если предположить, что количество объектов заведомо больше количества классов, то знаменатель растет быстрее, чем числитель, и, соответственно, значение выражения будет небольшим.

Несмотря на улучшение критерия выбора атрибута для разбиения, алгоритм может создавать узлы и листья, содержащие незначительное количество примеров. Чтобы избежать этого, следует воспользоваться еще одним эвристическим правилом: при разбиении множества Т по крайней мере два подмножества должны иметь не меньше заданного минимального количества объектов к(к> 1); обычно оно равно двум. В случае невыполнения данного правила дальнейшее разбиение этого множества прекращается и соответствующий узел отмечается как лист. При таком ограничении возможна ситуация, когда объекты, ассоциированные с узлом, относятся к разным классам. В качестве решения листа выбирается класс, который наиболее часто встречается в узле, если же примеров равное количество из всех классов, то решение дает класс, наиболее часто встречающийся у непосредственного предка данного листа.

Рассматриваемый алгоритм построения деревьев решений предполагает, что для переменной, выбираемой в качестве проверки, существуют все значения, хотя явно это нигде не утверждалось. То есть для любого примера из обучающей выборки существует значение по этой переменной.

Первое решение, которое лежит на поверхности, - не учитывать объекты с пропущенными значениями. Следует подчеркнуть, что крайне нежелательно отбрасывать весь объект только потому, что по одной из переменных пропущено значение, поскольку можно потерять много полезной информации.

Тогда необходимо выработать процедуру работы с пропущенными данными.

Пусть Т— обучающая выборка и X— проверка по некоторой переменной x. Обозначим через U количество неопределенных значений переменной х. Изменим формулы таким образом, чтобы учитывать только те объекты, у которых существуют значения по переменной x

В этом случае при подсчете freq(c_r, T) учитываются только объекты с существующими значениями переменной х.

Тогда критерий можно переписать:

Подобным образом изменяется и критерий gain ratio. Если проверка имеет п выходных значений, то критерий gain ratio считается как в случае, когда исходное множество разделено на п + 1 подмножеств.

Пусть теперь проверка x_h, с выходными значениями С_h1, C_h2,…, C_hm выбрана на основе модифицированного критерия.

Предстоит решить, что делать с пропущенными данными. Если объект из множества Т с известным выходом c_hi ассоциирован с подмножеством T_i вероятность того, что пример из множества T_i равна 1. Пусть тогда каждый объект из подмножества T_i, имеет вес, указывающий вероятность того, что объект принадлежит T_i,. Если объект имеет значение по переменной х, тогда вес равен 1, в противном случае объект ассоциируется со всеми множествами Т₁, Т₂... Т_m с соответствующими весами:

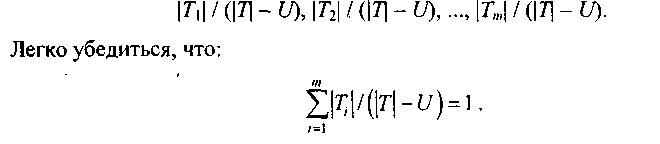
Вкратце этот подход можно сформулировать таким образом: предполагается, что пропущенные значения по переменной вероятностно распределены про­порционально частоте появления существующих значений.