Алгоритм Fuzzy c-Means

Данный алгоритм является обобщением предыдущего алгоритма. Его отличие состоит в том, что кластеры теперь являются нечеткими множествами и каждая точка принадлежит различным кластерам с различной степенью принадлежности. Точка относится к тому или иному кластеру по критерию максимума принадлежности данному кластеру.

Базовые понятия в данном случае имеют вид:

• обучающее множество

d— количество точек (векторов) данных;

• метрика расстояния (см. формулу (7.6));

• вектор центров кластеров

где

• • целевая функция

  

  

  

  матрица разбиения U = {u_tj}, где

• набор ограничений:

который определяет, что каждый вектор данных может принадлежать различным кластерам с разной степенью принадлежности, сумма принадлежностей элемента данных всем кластерам пространства разбиения равна единице.

Конструктивно алгоритм представляет собой итерационную процедуру следующего вида.

Шаг 1. Выбрать количество кластеров 2<c<d.

Шаг 2. Выбрать скалярную метрику для отображения векторов данных на естественную ось.

Шаг 3. Выбрать параметр остановки дельта.

Шаг 4. Выбрать коэффициент нечеткости, например w = 2.

Шаг 5. Проинициализировать матрицу разбиения (например, случайными значениями).

Шаг 6. Вычислить прототипы (центры) кластеров по формуле:

Шаг 7. Для всех элементов данных высчитать квадраты расстояний до всех (центров) кластеров по формуле:

(7.18)

Шаг 8. Обновить матрицу разбиения по следующей формуле:

учитывая ограничения из формулы (7.16).

Шаг 9. Проверить условие

. Если условие выполняется, завершить процесс, если нет — перейти к шагу 7 с номером итерации l= l + 1 •

Данный алгоритм имеет преимущества перед алгоритмом k-means, но обладает тем недостатком, что ищет кластеры сферической формы (рис. 7.7), что подходит далеко не для всех задач и поэтому зачастую неоправданно огрубляет результаты. От данного недостатка свободен следующий алгоритм.

Кластеризация по Гюстафсону-Кесселю

Данный алгоритм нечеткой кластеризации ищет кластеры в форме эллипсоидов (рис. 7.8), что делает его более гибким при решении различных задач.

Перед тем как описать данный алгоритм, обозначим дополнительные понятия, используемые в алгоритме.

Рис. 7.7. Форма кластеров в алгоритме Fuzzy C-Means

Рис. 7.8. Форма кластера в алгоритме кластеризации по Гюстафсону-Кесселю

Кластер характеризуется не только своим центром, но и ковариационной матрицей:

(7.20)

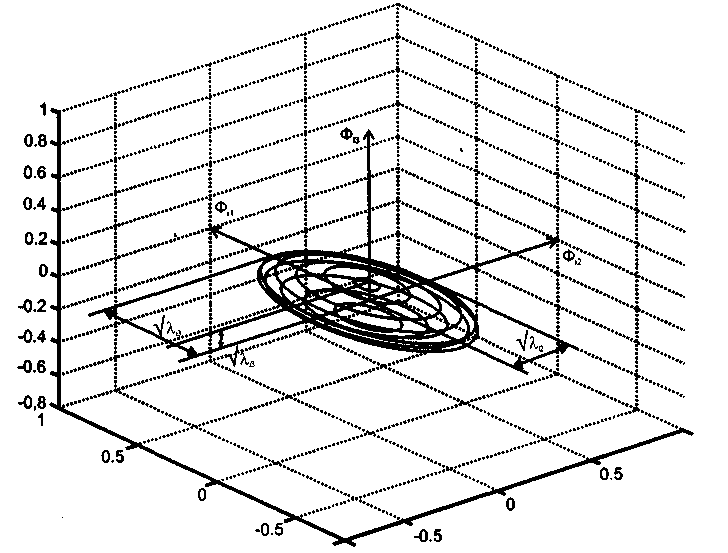
Рис. 7.9. Геометрическая иллюстрация к алгоритму кластеризации по Гюстафсону-Кесселю

Данный алгоритм использует свою нормирующую матрицу для вычисления расстояния. Выражения для вычисления выглядят следующим образом:

(7.21)

где

(7.22)

a F^(,) определяется по формуле (7.20).

который означает, что каждый вектор данных может принадлежать различным кластерам с разной степенью принадлежности, суммарная принадлежность элемента данных всем кластерам пространства разбиения рав­на единице.

Конструктивно алгоритм выглядит следующим образом.

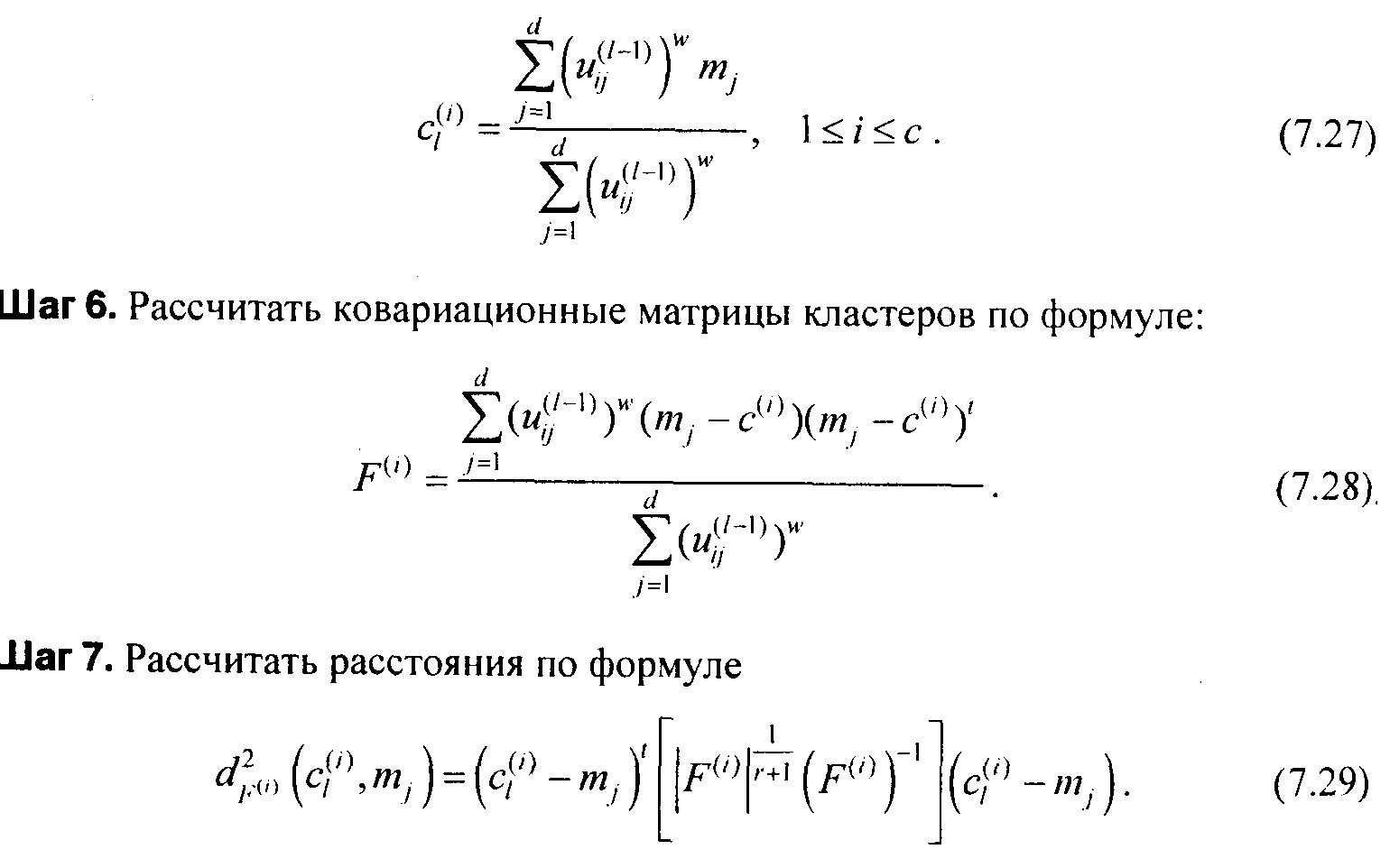
Шаг 8. Обновить матрицу по формуле:

(7.30)

с учетом следующих ограничений из формулы (7.26).

Шаг9. Проверить условие

Если условие выполняется, завершить процесс, если нет — перейти к шагу 5 с номером итерации l = l+ 1. В заключение данного этапа следует отметить, что приведенные алгоритмы не отличаются друг от друга подходом к кластеризации. Это становится очевидным при уравнении целевых функций, минимизация которых составляет сущность данных алгоритмов. Отличие заключается лишь в разных способах выведения расстояний между точками в пространстве входных данных. Алгоритмы расположены в порядке их усложнения. Так, каждый последующий алгоритм пытается учитывать все больше аспектов взаимосвязи данных. Существует некоторое количество алгоритмов, подобных описанным, единстве отличие которых заключается в дополнительных слагаемых целевой функции, которые учитывают некоторые другие аспекты взаимосвязи данных взаимное расположение кластеров, допущение о случайном характере растения точек внутри кластера, учет принадлежности тому или иному Мастеру ближайших соседей данной точки и др.). Однако важно заметить, главным слагаемым в этих целевых функциях является определенная ездоком двойная сумма

что свидетельствует о неизвестности основных допущений, на основании которых построены целевые функции. Основные из этих допущений выглядят следующим образом:

• кластеры в общем случае имеют форму эллипсоида;

• из предыдущего пункта следует, что у кластера всегда есть центр;

• отнесение точек к кластерам (разбиение) базируется на некотором расстоянии точек до центров кластера.

• из этих трех пунктов достаточно для определения недостатков данных алгоритмов:

допущение о том, что все кластеры всегда имеют некоторую, определяемую алгоритмом форму, а это, очевидно, далеко не всегда выполняется. Аппроксимация пространства входных данных некоторыми заданными фигурами на данных, имеющих сложное взаимное расположение, может привести к неинтерпретируемым результатам;

Допущение о том, что в кластере всегда есть некоторая узловая точка (центр кластера), степень принадлежности которой кластеру равна единице, в то время как остальные точки (не равные центру кластера) не могут принадлежать кластеру с такой же высокой степенью принадлежности, Что, опять, же, при сложном взаимном расположении точек данных является неприемлемым;

Такие алгоритмы строятся не на основе взаимного расположения точек, а не на отношении точек к центрам кластеров.

Основной иллюстрацией слабых сторон подобных алгоритмов кластеризации представляет случай, когда входные данные имеют форму двух вложенных Алгоритм Fuzzy C-Means, строящий сферические кластеры, не при каких условиях не разобьет пространство данных на два кластера, содержащих эти сферы.

Из перечисленных недостатков следует, что необходимо разработать такой подход к кластеризации данных, который бы учитывал взаимосвязь между точками данных, а не взаимосвязь точек и центров кластеров (которых в общем случае может в принципе не существовать). Такой подход может быть получен при помощи аппарата нечетких отношений, который еще не нашел широкого применения в алгоритмах кластеризации.

Для реализации указанного подхода необходимо исследовать как способы построения нечетких отношений, так и их свойства. Желательным результатом явилось бы получение аналога понятия классов эквивалентности, суще­ствующего в теории множеств для случая нечетких отношений.