Лабораторная работа фпэ–14 индуктивность

Цель работы: Изучение закона электромагнитной индукции, расчет индуктивности короткого соленоида, проверка закона Ома для цепи постоянного и переменного тока с индуктивностью и активным сопротивлением, экспериментальное определение индуктивности короткого соленоида и магнитной проницаемости сердечника.

Приборы и принадлежности: лабораторная установка для проведения опытов.

Теоретическая часть

1. Если проводящий контур поместить в переменное магнитное поле (рис.14.1), то в этом контуре возникает электродвижущая сила индукции, численно равная скорости изменения потока магнитной индукции через поверхность S, стягиваемую контуром (закон Фарадея):

, (14.1)

Поток магнитной индукции может изменяться как в результате движения в неоднородном магнитном поле, так и за счет изменения индукции магнитного поля во времени, что учитывается полной производной в формуле (14.1).

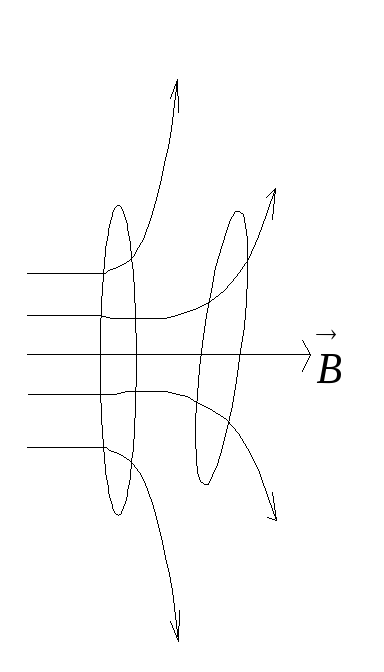
Рис.14.1: Проводящий виток в магнитном поле

Знак минус выражает правило Ленца: индукционный ток в контуре направлен таким образом, что создаваемый им поток магнитной индукции через поверхность S противодействует изменению внешнего магнитного потока, который вызвал этот ток.

Если внешнего поля нет, а по контуру течет переменный ток i, то в нем также возникает э.д.с. Это явление называется самоиндукцией. Поток магнитной индукции через контур в этом случае пропорционален току

(14.2)

а закон Фарадея (14.1) можно записать в виде:

(14.3)

Коэффициент пропорциональности L называется индуктивностью контура и при условии зависит только от его геометрических характеристик. Определяется индуктивностьL на основании закона Био-Савара-Лапласа с учетом выражения (14.1) для потока вектора магнитной индукции:

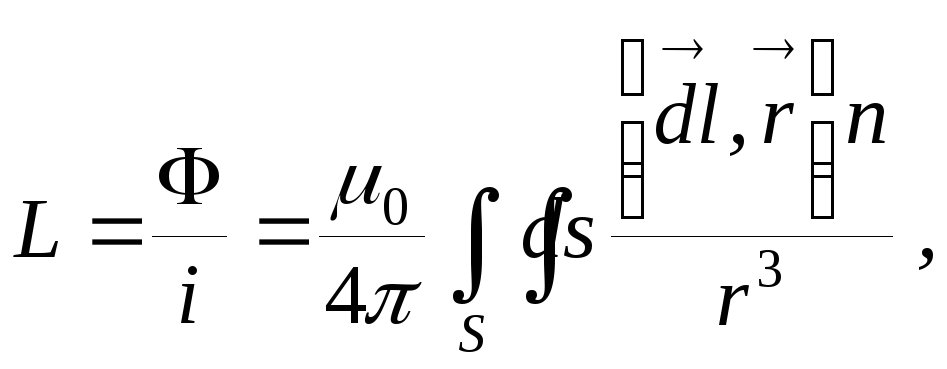(14.4)

где – магнитная постоянная,– радиус-вектор, проведенный из элементаконтура в элементds поверхности S, ограниченной этим контуром, индекс “n” означает проекцию на нормаль к поверхности S.

2. Рассмотрим применение формулы (14.4) на примере короткого соленоида-катушки, длина которой l соизмерима с поперечным размером  (рис.14.2). Магнитная индукция поля в точке O соленоида, создаваемая участком dx длины соленоида равна

(14.5)

где – индукция поля, создаваемая одним витком,n – плотность намотки. Величину можно определить на основании закона Био-Савара-Лапласа:

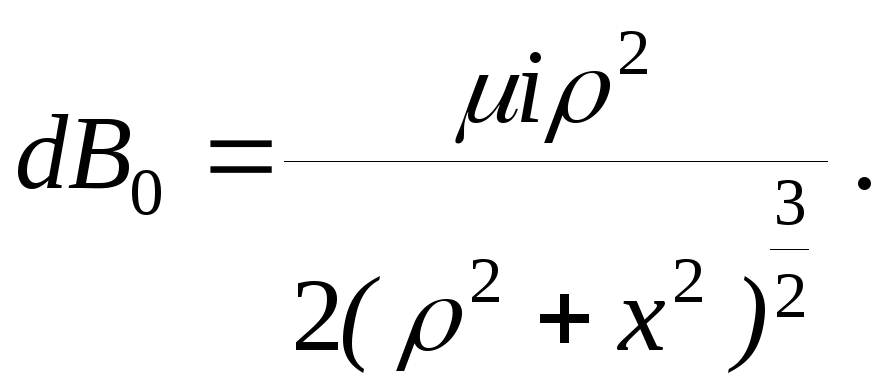(14.6)

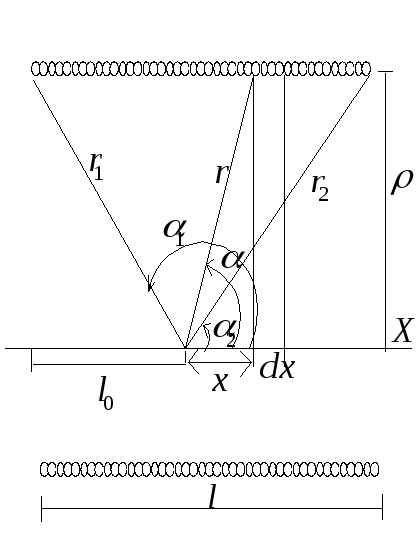
Рис.14.2: Схема короткого соленоида-катушки

Тогда 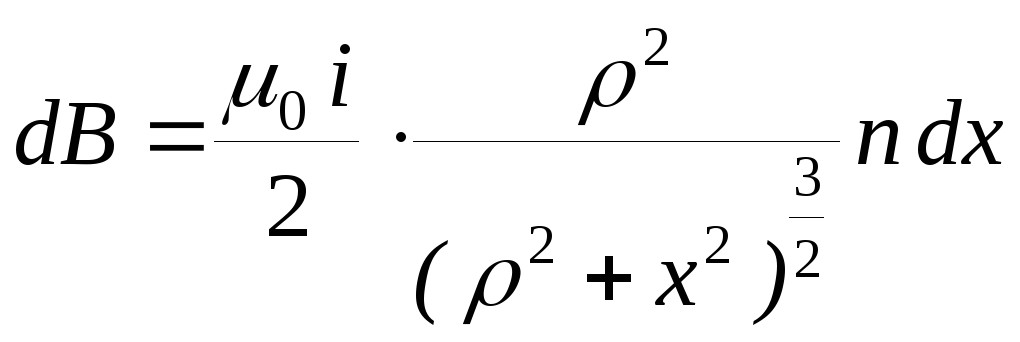(14.7)

Интегрирование по всем виткам осуществим с учетом тригонометрической замены , в результате чего получим величину индукции магнитного поля на оси соленоида:

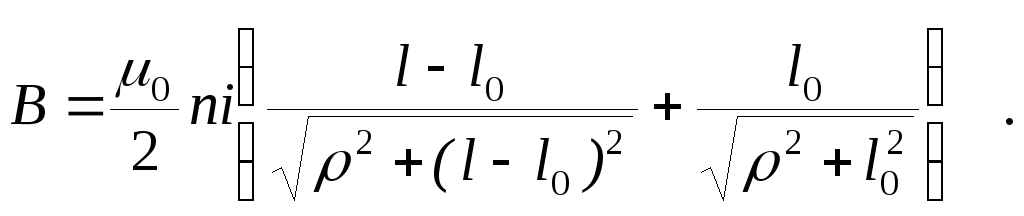(14.8)

Если при вычислении потока магнитной индукции через соленоид учитывается не только зависимость В от , но и неоднородность поля по сечению, то расчеты значительно усложняются. Поэтому приведем здесь лишь одну из приближенных формул для расчета индуктивности короткого соленоида:

(14.9)

Из (14.9) для длинного соленоида (<<l) получим:

(14.10)

Если катушка заполнена магнетиком с проницаемостью , то

(14.11)

(14.12)

3. Если электрическая цепь (рис.14.3), состоит из катушки индуктивности L с активным сопротивлением и источника переменного напряжения, то в ней течет токi, изменяющийся по закону:

(14.13)

с амплитудой и начальной фазой:

(14.14)

(14.15)

Зависимость (14.14) представляет закон Ома для цепи переменного тока. Если по цепи течет постоянный ток, то  = 0 и соотношения (14.14), (14.15) переписываются в виде:

(14.16)

Таким образом, проводя электрические измерения в контуре на постоянном и переменном токе, можно получить параметры катушки индуктивности и магнитного сердечника.