
-
Линейное приближение уравнений, описывающих движения вблизи положения равновесия.
Будем предполагать, что в уравнениях Лагранжа, описывающих движение
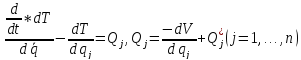 (2.1)
(2.1)
все
непотенциальные части обобщенных
сил 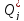 являются
функциями только q
и
являются
функциями только q
и
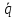 и
не зависят явно от t.
и
не зависят явно от t.
Пусть 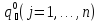 —
исследуемое положение равновесия.
Переместим начало координат в точку
—
исследуемое положение равновесия.
Переместим начало координат в точку
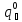 ,
т. е. будем считать, что
,
т. е. будем считать, что 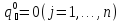 и
что
и
что 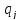 —
отклонения обобщенных координат от их
равновесных значений. Тогда в 2n-мерном
фазовом пространстве q,
—
отклонения обобщенных координат от их
равновесных значений. Тогда в 2n-мерном
фазовом пространстве q,
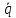 положению равновесия тоже соответствует
начало координат, так как при равновесии
все q равны нулю.
положению равновесия тоже соответствует
начало координат, так как при равновесии
все q равны нулю.
Исследуя
движения, происходящие в малой окрестности
положения равновесия, мы будем считать,
что во время таких движений все 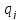 и
и
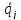 —
малые величины одного и то же порядка
малости. Ограничимся в уравнениях лишь
малыми первого порядка и пренебрежем
малыми второго и более высоких порядков.
—
малые величины одного и то же порядка
малости. Ограничимся в уравнениях лишь
малыми первого порядка и пренебрежем
малыми второго и более высоких порядков.
Чтобы
сохранить в этих уравнениях лишь малые
первого порядка, разложим функции Т, V
и 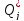 в
ряды по всем независимым переменным q
и
в
ряды по всем независимым переменным q
и 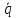 и
ограничимся в разложениях Т и V малыми
второго порядка, а в разложении
и
ограничимся в разложениях Т и V малыми
второго порядка, а в разложении 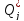 —
малыми первого порядка.
—
малыми первого порядка.
В рассматриваемом стационарном случае

и
чтобы сохранить в разложении Т лишь
малые второго порядка, надо разложить
в ряды коэффициенты 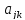 и
ограничиться в этих разложениях
«нулевыми» членами, не содержащими
множителей
и
ограничиться в этих разложениях
«нулевыми» членами, не содержащими
множителей 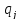 , т.
е. положить
, т.
е. положить

Обозначим
полученные так величины через 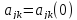 тогда
тогда
 (2.2)
(2.2)
Это
выражение является квадратичной формой
от обобщенных скоростей с постоянными
коэффициентами. Из физического смысла
понятия кинетической энергии следует,
что функция Т равна нулю лишь тогда,
когда все 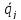 одновременно
равны нулю, и положительна, если хотя
бы одна из
одновременно
равны нулю, и положительна, если хотя
бы одна из  отлична
от нуля. Квадратичная форма, удовлетворяющая
этим условиям, называется положительно
определенной, а матрица, составленная
из ее коэффициентов,
отлична
от нуля. Квадратичная форма, удовлетворяющая
этим условиям, называется положительно
определенной, а матрица, составленная
из ее коэффициентов,
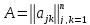
называется матрицей положительно определенной квадратичной формы, или просто положительно определенной матрицей.
Обратимся теперь к выражению для обобщенной силы
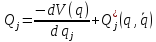
и разложим это выражение в ряд

 (2.3)
(2.3)
где многоточием заменены остальные (нелинейные) члены разложения. Величина, стоящая в первой квадратной скобке, равна нулю, так как она равна значению обобщенной силы в положении равновесия
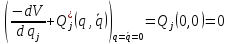
Введем обозначения


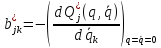
Пренебрегая в разложении (2.3) нелинейными членами и используя только что введенные обозначения, получаем
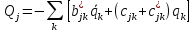 (2.4)
(2.4)
Подставим
теперь в уравнения Лагранжа (2.1) выражения
(2.2) и (2.4) для Т и 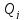 соответственно:
соответственно:
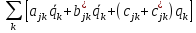 (2.5)
(2.5)
В векторно-матричной записи эта система уравнений имеет вид
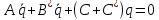 (2.6)
(2.6)
здесь A,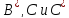 —
квадратные матрицы, составленные из
элементов
—
квадратные матрицы, составленные из
элементов  соответственно,
a q является n-мерным
вектором-столбцом, составленным из
обобщенных координат.
соответственно,
a q является n-мерным
вектором-столбцом, составленным из
обобщенных координат.
Линейные дифференциальные уравнения (2.5) (или (2.6)) называются уравнениями линейного приближения. Они приближенно описывают движения, происходящие в малой окрестности положения равновесия. Уравнения линейного приближения (2.5) сами по себе не определяют размеров области, в пределах которой точные нелинейные уравнения (2.1) могут быть заменены этими линейными уравнениями.
Границы
этой области зависят от отброшенных
нами членов высшего порядка в разложениях
функций Т, V и 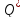 .
В частных случаях может оказаться, что
эта область весьма велика, например,
заведомо охватывает все возможные
движения системы.
.
В частных случаях может оказаться, что
эта область весьма велика, например,
заведомо охватывает все возможные
движения системы.
Вернемся к уравнениям линейного приближения (2.6). Из теории дифференциальных уравнений известно, что решение системы уравнений (2.6) имеет вид
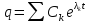
где
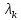 -корни уравнения
-корни уравнения
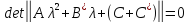 (2.7)
(2.7)
которое называется характеристическим уравнением линейного приближения. Каждый элемент этого определителя n-го порядка является квадратичным полиномом относительно λ; поэтому левая часть характеристического уравнения линейного приближения — характеристический полином — представляет собой полином степени m=2n.
Уравнения (2.6) отличаются от общего случая системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами только тем, что матрица А не произвольна, а всегда является матрицей положительно определенной квадратичной формы.
Выделим теперь два частных случая, когда уравнения (2.6) принимают более специальный вид.
Консервативная
система. В случае консервативной
системы 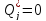 ,
поэтому все
,
поэтому все 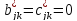 и
уравнения линейного приближения (2.6)
сводятся к виду
и
уравнения линейного приближения (2.6)
сводятся к виду
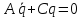 (2.8)
(2.8)
Характеристическое уравнение (2.7) соответственно имеет вид
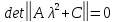 (2.9)
(2.9)
Если дополнительно предположить, что не только А, но и С является матрицей положительно определенной квадратичной формы, то все корни характеристического уравнения (2.9) будут чисто мнимыми.
Диссипативная
система. Пусть теперь 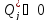 ,
но зависят лишь от обобщенных скоростей.
В этом случае вблизи положения равновесия
,
но зависят лишь от обобщенных скоростей.
В этом случае вблизи положения равновесия
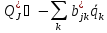
и
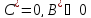
Разумеется,
система является диссипативной не
всегда, т. е. не при любом выборе чисел 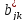 .
Найдем условия, которым должны
удовлетворять числа
.
Найдем условия, которым должны
удовлетворять числа 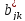 Для
того, чтобы система была диссипативной.
С этой целью введем квадратичную форму
Для
того, чтобы система была диссипативной.
С этой целью введем квадратичную форму
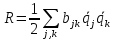 (2.10)
(2.10)
тогда
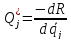 (2.11)
(2.11)
Функция R называется функцией Релея.
Если рассматриваемая система диссипативна, то
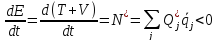
где 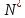 —
мощность непотенциальных сил.
—
мощность непотенциальных сил.
Но в силу (2.11) и теоремы Эйлера[6] об однородных функциях
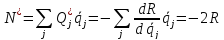
и
из условия  следует,
что
следует,
что 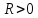 ,
если хоть одна обобщенная скорость
,
если хоть одна обобщенная скорость
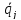 отлична от нуля.
отлична от нуля.
Таким образом, для диссипативной системы функция Релея является положительно определенной квадратичной формой, и в уравнениях движения
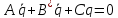
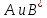 будут
матрицами положительно определенных
квадратичных форм.
будут
матрицами положительно определенных
квадратичных форм.
