Л.А. Штраус - Пределы
.doc
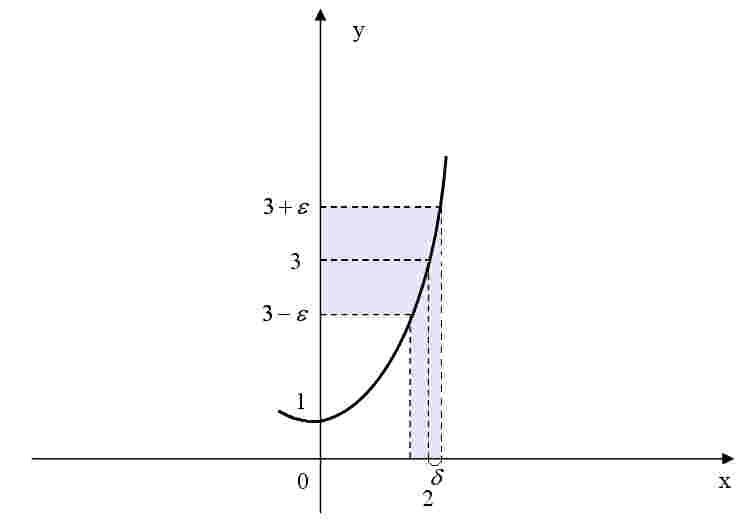
Рис.1
3-й
способ. Найдём
по
графически (см. рис. 1) и получим такой
же результат, как для второго способа
(в этом легко убедиться самостоятельно).
Пример
39. С
помощью «
»
рассуждений доказать непрерывность
следующих функций: 1)
:2)
.
Решение.
1).
Пусть
Тогда
если
.
Кроме того, должно выполняться условие
,откуда
и
При а=0
если
( в качестве окрестности нуля в множестве
Е=D(f)
берётся
).
2). Покажем, что для любых х и а
(15)
Из определения арктангенса и с помощью замены переменной получаем, что это неравенство равносильно неравенству
где
(16)
Если
х и а одного знака, то
Мы
воспользовались известным неравенством
Из него же следует справедливость (16)
для х и а разного знака. Из неравенства
(15)следует, что в качестве искомого
можно взять
:
если
,
то получаем, что
Пусть
функция
определена
в точках некоторой окрестности точки
а, кроме, быть может, самой точки а.
Определение.
Точка а называется точкой разрыва
функции
,
если она не определена в точке а или
определена в этой точке, но не является
в ней непрерывной.
Если
а – точка разрыва и существуют конечные
пределы
и
,
то а называется точкой разрыва первого
рода. Если при этом
,
то а называется точкой устранимого
разрыва.
Точки
разрыва функции
,
не являющиеся точками разрыва первого
рода, называются точками разрыва второго
рода. Если при этом
или
,
то а называется точкой бесконечного
разрыва.
Если
в некоторой полуокрестности слева или
справа от а
не определена, то для определения
характера разрыва рассматривают только
или
.
Пример
40.
Найти точки разрыва функции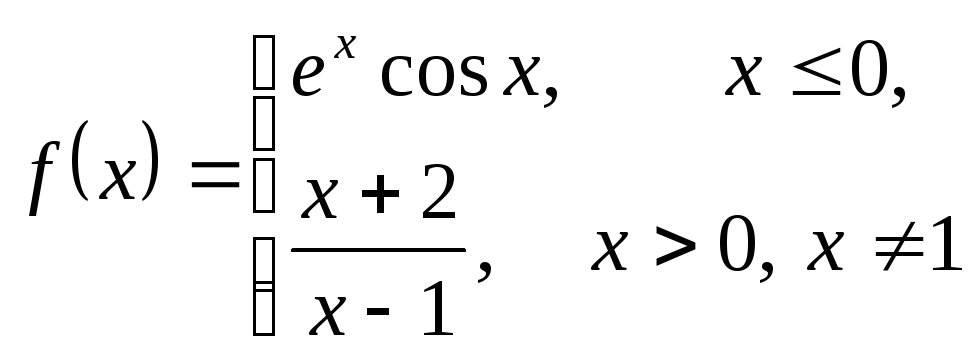
и исследовать их характер.
Решение.
В точках
функция непрерывна, поскольку является
произведением или частным непрерывных
функций. В точке
оба односторонних предела существуют
и не равны:
.
Следовательно,
- точка разрыва первого рода. В точке
х=1
,
следовательно,
- точка разрыва второго рода
( точка бесконечного разрыва).
Пример
41.
Определить точки разрыва функции
и исследовать их характер.
Решение.
Находим область определения
функции:
Отсюда
или
. На
функция непрерывна: на множестве
в силу арифметических свойств и
непрерывности корня, а в точках
- поскольку они являются изолированными
(отдельными) точками
.
Таким образом, точками разрыва могут
быть только
.
Находим
.
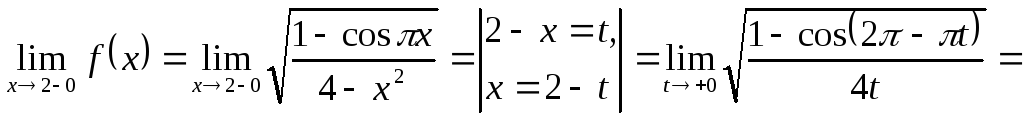
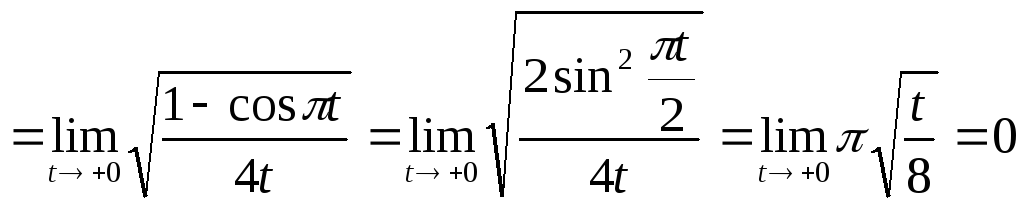Поскольку
чётная,
то и
.
Следовательно,
- точки устранимого разрыва.
Пример
42.
Исследовать на непрерывность функцию
и построить её график.
Решение.
Пусть х>0. При х>1
и у=0. При
у=1. При
и
Таким образом, при
(одновременно
строим график, рис. 2 );
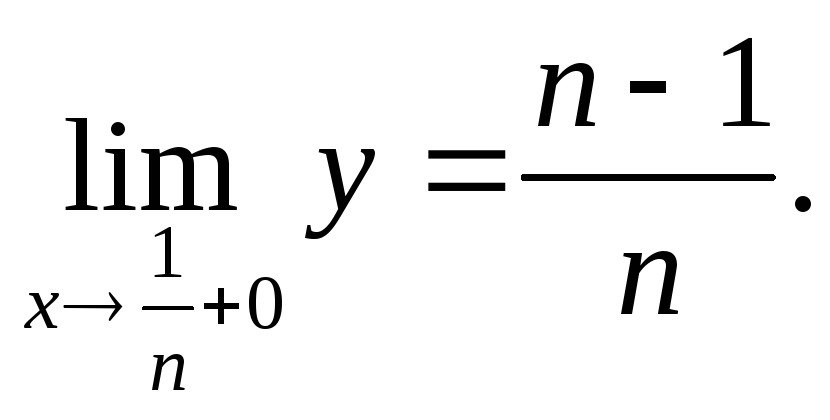Следовательно,
,
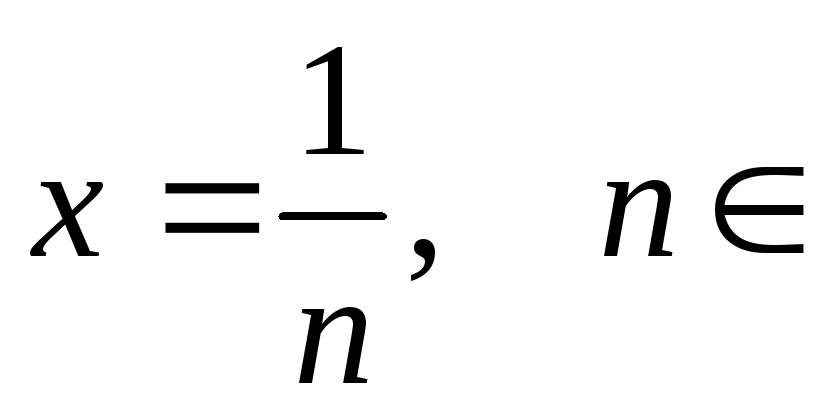
являются для у точками разрыва первого
рода. Пусть теперь х<0. При х < -1
и
.
При
,
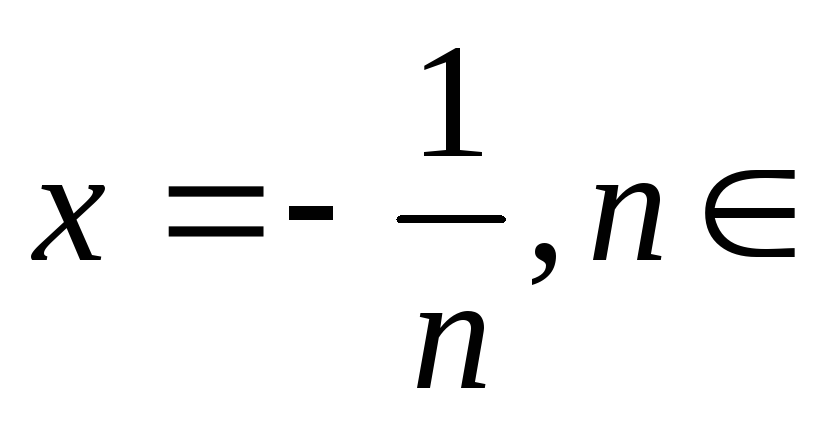
у=1. При
и
Таким образом, при
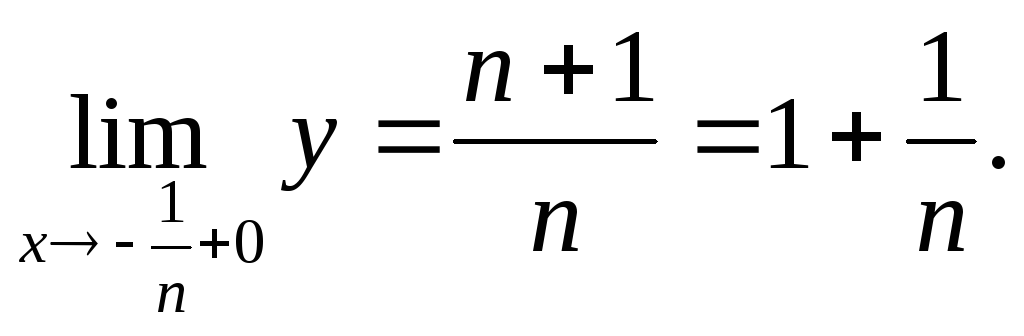Получаем, что и точки
,
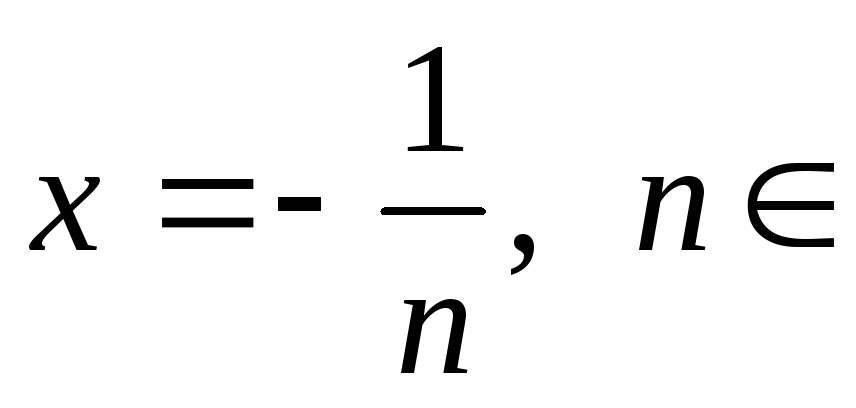
являются точками разрыва первого рода.
Поскольку
то х=0 является точкой устранимого
разрыва. Во всех остальных точках функция
непрерывна.
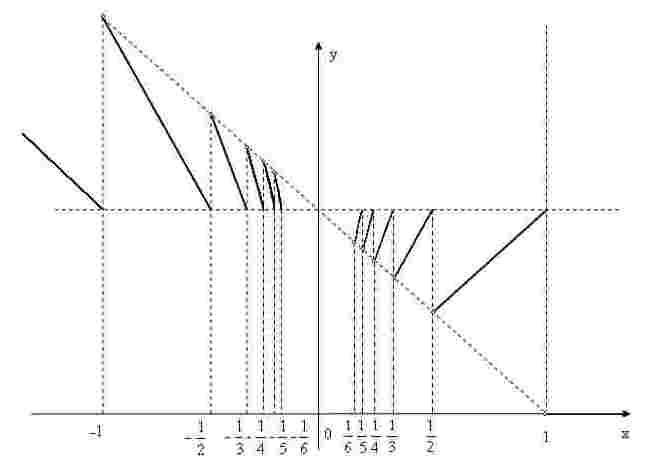
Рис. 2
Л И Т Е Р А Т У Р А
-
Демидович Б.П. Сборник задач и упражнений по математическому анализу: Учеб.пособие для вузов.- М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2002.- 558 с.
-
Ляшко И.И., Боярчук А.А., Гай Я.Г., Головач Г.П. Математический анализ в примерах и задачах, ч.1. Введение в анализ, производная, интеграл. – Киев, Издательское объединение «Вища школа», 1974.-680 с.
-
Кузнецов Л.А. Сборник задач по высшей математике. Типовые расчёты: Учебное пособие. 3-е изд., испр.-СПб.: Издательство «Лань», 2005. -240 с.
-
Кузнецова М.Г. Типовой расчёт по высшей математике: Пределы.- Ульяновск: УлПИ, 1987.- 24 с.