Л.А. Штраус - Пределы

Ульяновский государственный университет

Кафедра алгебро-геометрических вычислений

Л.А. Штраус, И.В. Баринова

П Р Е Д Е Л Ы

Методические указания для студентов факультета математики

и информационных технологий и факультета управления

Ульяновск-2007

Штраус Л.А., Баринова И.В. Пределы. Ульяновск: УлГУ.-2007.

Методические указания составлены в соответствии с учебными программами курсов математического анализа для факультета математики и информационных технологий и факультета управления и относятся к разделу «Введение в анализ». Они будут способствовать усвоению теоретического материала и формированию вычислительных навыков у студентов первого курса по одной из первых тем дисциплины, преодолению разрыва между уровнем математической подготовки выпускников средней школы и требованиями, предъявляемыми к уровню знаний студентов. Рассматриваемые задачи занимают максимально широкий диапазон - от простейших упражнений, соответствующих сборнику [3](по которому можно составлять индивидуальные семестровые задания) и контролирующих формирование необходимых вычислительных навыков, до серьёзных задач из сборника [1]. В последнем случае предлагаемые решения классических задач не копируют решений из [2] и соответствуют логике изучения дисциплины. Некоторые понятия, обязательные для изучения на факультете математики и информационных технологий (верхний и нижний пределы последовательности, равномерная непрерывность функции и др.) не рассматриваются в данных указаниях. Однако многие из основных определений здесь приведены. Перед их применением необходимо ознакомиться с соответствующим материалом по конспекту лекций или учебнику.

Предел последовательности

Определение. Число а называется пределом последовательности , если для любого существует номер N такой, что при всех n>N выполняется неравенство

( ).

Пример 1. Доказать, что (указать ).

Решение. Неравенство из определения предела последовательности, которое мы должны решить относительно n, принимает вид Пусть . Тогда, откуда , следовательно, в качестве N можно взять . Здесь - целая часть числа , то есть наибольшее целое число, не превосходящее . Если, например, , то условиям задачи отвечают натуральные числа , то есть

Пример 2. Доказать, что (указать ).

Решение. Неравенство принимает вид , Последнее неравенство преобразуется в квадратное. Однако вычисления можно упростить. Неравенство будет выполняться, если справедливо следующее двойное неравенство: Его левая часть заведомо выполняется при . Правая часть выполняется при . Следовательно, условиям задачи отвечают числа Отсюда

При вычислении предела в случае и (т.е. в случае неопределённости вида ) или в случае, и т.д. нельзя сразу воспользоваться арифметическими свойствами предела. Следует так преобразовать выражение , чтобы можно было использовать свойства предела и раскрыть неопределённость, т.е. найти предел. Полезным для этого в случае бывает вынести в числителе и знаменателе старшие степени за скобки или разделить числитель и знаменатель на старшую степень одного из них.

Пример 3. Найти предел .

Решение. Преобразуем исходное выражение, выполнив действия в числителе и знаменателе:

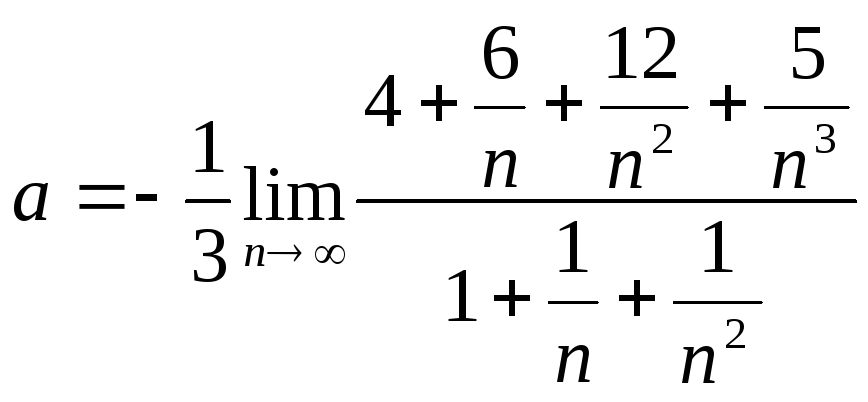. Разделив числитель и знаменатель на их старшую степень , получим . Поскольку то по свойствам предела получаем

Вообще предел отношения двух многочленов переменной можно находить по правилу

(1)

так что в решении последнего примера можно было обойтись без деления на .

При вычислении пределов используют формулу бинома Ньютона

(2)

Также следует знать формулу ( «эн-факториал»- произведение натуральных чисел от 1 до n; например, ).

Пример 4. Найти предел .

Решение. Разделим числитель и знаменатель исходного выражения на -

старшую степень числителя и знаменателя. Действительно, показатель степени суммы равен наибольшему показателю степени слагаемых, поэтому для числителя он равен 2 (). Показатель степени произведения равен сумме показателей степеней сомножителей. Показатели степени выражений равны 1, поэтому показатель степени знаменателя равен 1+1=2. Тогда Поскольку при то 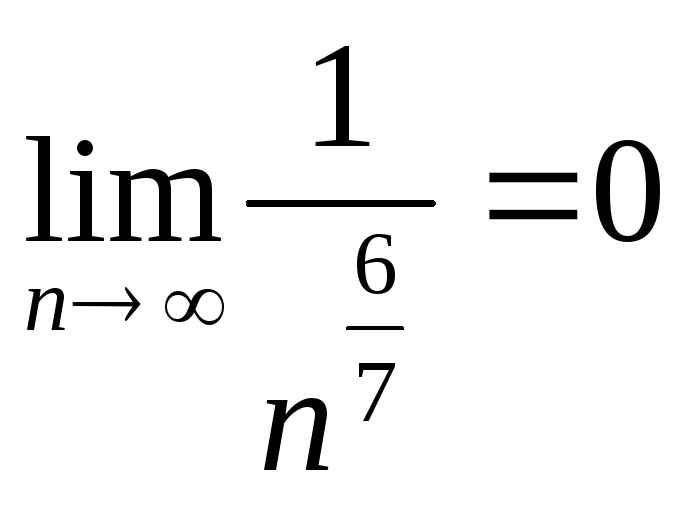, и по свойствам предела получаем

При вычислении пределов, содержащих иррациональные выражения, часто используют приём перевода иррациональности из числителя в знаменатель или наоборот с помощью формул сокращённого умножения

(3)

(4)

(5)

(первая и вторая из них получаются из третьей при и соответственно).

Так, например, если выражение содержит множитель , где и и их старшие степени и коэффициенты при них совпадают или эта разность стремится к нулю, полезно умножить числитель и знаменатель исходной дроби на , т.е. на выражение, сопряжённое к .

Пример 5. Найти предел

Решение. Имеем неопределённость.Умножим числитель и знаменатель дроби на выражение, сопряжённое к числителю и воспользуемся формулой (3); далее разделим числитель и знаменатель на :

Теперь воспользуемся арифметическими свойствами предела и тем, что при

Замечание. Сразу после (6) можно было записать, поскольку показатели степени слагаемых в знаменателе и равны 3, следовательно, старшая степень знаменателя есть и коэффициент при равен 2 (на языке асимптотического поведения функций выражение в знаменателе эквивалентно , то есть

, эквивалентно , а при вычислении пределов величины можно заменять на эквивалентные, см. с. ).

Пример 6. Найти предел

Решение. Имеем неопределённость. Воспользуемся формулой (4).Умножим числитель и знаменатель дроби на выражение, дополняющее числитель до разности кубов, то есть на соответствующий неполный квадрат суммы; далее разделим числитель и знаменатель на и воспользуемся арифметическими свойствами предела:

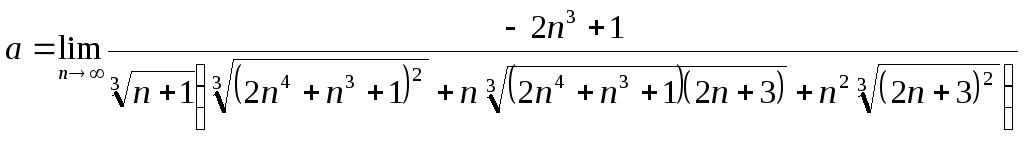. (7)

Замечание. Сразу после (7) можно было записать (см. предыдущее замечание).

Пример 7. Найти предел

Решение. Поскольку , то . Первый сомножитель в числителе является суммой геометрической прогрессии. Найдём эту сумму по формуле : 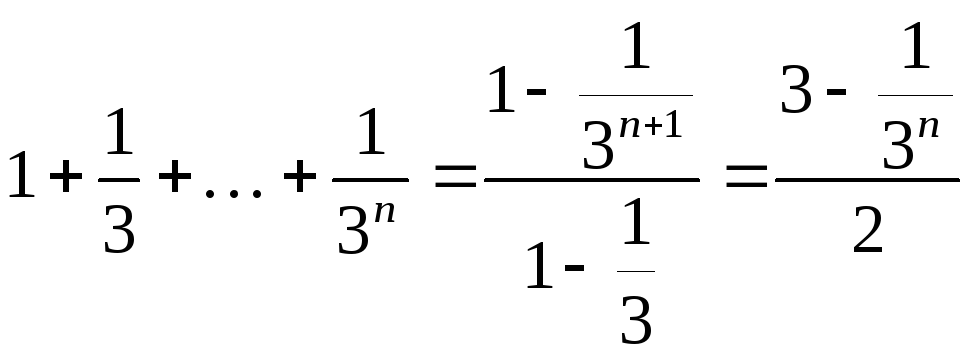. Так как , то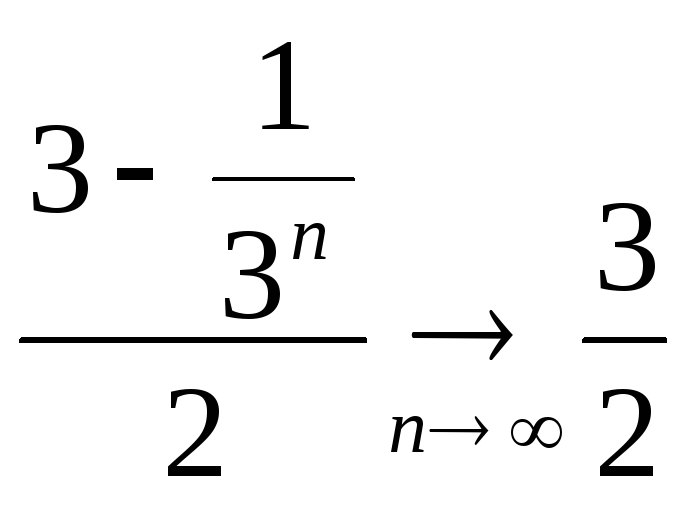. Окончательно получаем

Пример 8. Найти предел

Решение. Воспользуемся формулой суммы арифметической прогрессии : . Кроме того, , откуда . Подставляем полученные выражения в исходное:

.

Разделим теперь числитель и знаменатель последовательно на и :

^{поскольку}

Пример 9. Найти предел

Решение. Обозначим Если - чётное, , то Если - нечётное, , то

Таким образом, при любом Поскольку то .

Задачи, связанные с применением теоремы Вейерштрасса о пределе монотонной последовательности.

Пример 10. Доказать, что

Решение. 1-й способ. Обозначим Заметим, что при Поэтому последовательность убывает при и, поскольку она ограничена снизу нулём, то имеет предел. Обозначим и перейдём к пределу в равенстве

2-й способ. Используя формулу (2), получаем Отсюда Поскольку , из последнего неравенства следует, что

3-й способ. Найдём , при которых выполняется неравенство Следовательно, при

, то есть . Поскольку то из последнего неравенства следует, что .

Пример 11. Доказать, что последовательность монотонно возрастает и ограничена сверху, а последовательность монотонно убывает и ограничена снизу. Отсюда вывести, что эти последовательности имеют общий предел .

Второй замечательный предел

задаётся формулами , , где

или формулой (). Он применяется, в частности, при вычислении пределов

, где т.е. в случае неопределённости вида

Пример 12. Найти предел

Решение. Находим пределы основания и показателя степени исходного выражения и убеждаемся в том, что перед нами неопределённость вида Выделяем в исходном выражении формулу и вычисляем предел.

Пример 13. Пользуясь критерием Коши, доказать расходимость последовательности

Пример 14. Доказать, что

Решение. Покажем, что при любом

Действительно, это неравенство равносильно неравенствам

Последнее неравенство верно, поскольку последовательность

убывает(см. пример ) и её предел равен Тогда

Поскольку то и

Пример 15. Для нахождения применяется следующий процесс: произвольно,

(8)

Доказать, что

Решение. Из известного неравенства , связывающего среднее арифметическое и среднее геометрическое двух неотрицательных чисел, получаем, что для любого Теперь убедимся в том, что последовательность не возрастает. Действительно, неравенство то есть , равносильно , . В справедливости последнего неравенства мы убедились выше. По теореме Вейерштрасса последовательность имеет предел , который находим, переходя в (8) к пределу: , .

Пример 16. Последовательность определяется следующим образом:

, Найти .

Решение. Оценим разность между и числом , являющимся корнем уравнения : , . Применяя полученное неравенство к разности и т.д., получим , .

Поскольку , то и .

Предел функции

Пусть Е- некоторое непустое подмножество множества R действительных чисел, – предельная точка множества Е, - функция, определённая на Е.

Определение. Число называется пределом функции в точке , если

>0   ). (9)