МатМод экология / Лекция №8

Лекция №8

Персептроны.

Сети, о которых пойдет речь в этой лекции, являются основной

"рабочей лошадкой" современного нейрокомпьютинга. Подавляющее большинство приложений связано именно с применением таких многослойных персептронов или для краткости просто персептронов

(название происходит от английского perception - восприятие, т.к. первый образец такого рода машин предназначался для моделирования зрения). Как правило, используются именно сети, состоящие из последовательных слоев нейронов.

Персептрон Розенблатта

Первой моделью нейросетей считают однослойный персептрон Розенблатта. Однослойный персептрон способен распознавать простейшие образы.

x1

y1

x2

y2

x3

y3

x4

Рис. 8.1. Однослойный персептрон Розенблатта с тремя входами и тремя нейронами в слое.

Каждый нейрон вычисляет взвешенную сумму элементов входного сигнала, отнимает значение сдвига и пропускает результат через жесткую пороговую функцию, выход которой равняется +1 или -1. На рис. 8.2

показана схема нейронов, используемых в однослойных персептронах, и

график передаточной функции:

Рис. 8.2. Схема нейрона, график передаточной функции

Простейший персептрон состоит из нескольких входов и единственного выхода, и, по сути, представляет собой единичный нейрон с пороговой функцией:

Рис. 8.3. Персептрон с единственным выходом.

Простейший персептрон может дать простейший ответ типа «да» или

«нет» (говорят: «принадлежит ли входной вектор к классу А или к классу В»). В зависимости от значения выходного сигнала принимается решение:

+1 - входной сигнал принадлежит классу A (ответ «да»),

-1 - входной сигнал принадлежит классу B (ответ «нет»).

На рисунке 8.3. показан случай, когда размерность входного сигнала равняется 2, т.е. для входного вектора (x1, x2) . При этом разделяющая поверхность представляет собой прямую линию на плоскости. Уравнение,

задающее разделяющую прямую, зависит от значений синоптических весов и сдвига.

Рис. 8.3. Разделяющая поверхность, порожденная персептроном.

Если в выходном слое присутствует несколько нейронов, персептрон может определять большее количество классов. Например, персептрон с двумя выходами:

x1

y1

x2

y2

x3

x4

Рис. 8.4. Персептрон с двумя выходами.

может относить любой входной вектор уже к четырем возможным классам:

Алгоритм обучения однослойного персептрона

Пусть персептрон состоит из n входных (i=1..n) и m выходных (j=1..m)

сигналов.

1.Инициализация синоптических весов и сдвига: синоптические веса принимают небольшие случайные значения. Дискретное время обучения t принимается равным нулю: t=0.

2.Предъявление сети нового входного и желаемого выходного сигналов:

Входной сигнал x=(x1, x2, ..., xn) предъявляется нейрону вместе с желаемым выходным сигналом d=(d1, d2,…dm).

3.Вычисление сигналов выходных нейронов:

где wіj(t) - вес связи от і-го элемента входного сигнала к j-тому выходному нейрону в момент времени t, r - скорость обучения (меньше

1); dj(t) - желаемый выходной сигнал на j-том нейроне. Если сеть принимает правильное решение, синоптические веса не модифицируются.

5.Переход к шагу 2.

Тип входных сигналов: бинарные или аналоговые.

классификация.

Недостатки. Примитивные разделяющие поверхности

(гиперплоскости) дают возможность решать лишь простейшие задачи

распознавания.

Преимущества. Программные и аппаратные реализации модели очень просты. Простой и быстрый алгоритм обучения.

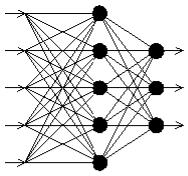
Модификации. Многослойные персептроны дают возможность

строить более сложные разделяющие поверхности, и потому более

распространены.

Многослойный персептрон с обратным распространением ошибки

Типичная сеть ВackРropagation имеет входной слой, выходной слой и по крайней мере один скрытый слой. Теоретически, ограничений относительно числа скрытых слоев не существует, но практически применяют один или два.

Рис. 8.5. Многослойный персептрон с одним скрытым слоем.

Нейроны организованы в послойную структуру с прямой передачей сигнала. Каждый нейрон сети продуцирует взвешенную сумму своих входов,

пропускает эту величину через передаточную функцию и выдает выходное значение. Сеть может моделировать функцию практически любой сложности, причем число слоев и число нейронов в каждом слое определяют сложность функции. Определение числа промежуточных слоев и числа нейронов в них является важным при моделировании сети. Большинство исследователей и инженеров, применяя архитектуру к определенным проблемам, используют общие правила, в частности:

1.Количество входов и выходов сети определяются количеством входных и выходных параметров исследуемого объекта, явления,

процесса, и т.п. В отличие от внешних слоев, число нейронов скрытого слоя выбирается эмпирическим путем. В большинстве случаев достаточное количество нейронов составляет nск ≤ nвх + nвых, где nвх, nвых - количество нейронов во входном и, соответственно, в выходном слоях.

2.Если сложность в отношении между полученными и желаемыми данными на выходе увеличивается, количество нейронов скрытого слоя должна также увеличиться.

3.Если моделируемый процесс может разделяться на несколько этапов,

нужен дополнительный скрытый слой для каждого этапа. Если процесс не разделяется на этапы, тогда дополнительные слои могут вызвать перезапоминание и, соответственно, неверное общее решение.

Существует и более строгое обоснование выбора количества скрытых слоев и числа нейронов в каждом из них. Теорема Колмогорова о достаточной структуре нейронной сети гласит: Для трансформации N-

мерного входного вектора множества входных данных x в M-мерный выходной вектор d достаточно использование нейросети с одним скрытым слоем. При N входных нейронах для реализации аппроксимирующей функции достаточно использовать в скрытом слое (2N+1) нейронов.

После того, как определено число слоев и число нейронов в любом из них, нужно найти значения для синаптических весов и порогов сети,

способных минимизировать погрешность результата. Именно для этого существуют алгоритмы обучения, где происходит подгонка модели сети к имеющимся обучающим данным. Погрешность для конкретной модели сети определяется путем прохождения через сеть всех обучающих примеров и сравнения спродуцированних выходных значений с желаемыми значениями.

Множество погрешностей создает функцию погрешностей, значение которой

можно рассматривать как погрешность сети в целом. В качестве функции погрешностей чаще используют сумму квадратов погрешностей:

В качестве аргумента функции ошибки выступают значения синаптических весов.

Алгоритм обучения действует итеративно, его шаги называются эпохами. На каждой эпохе на вход сети поочередно подаются все обучающие примеры, выходные значения сети сравниваются с желаемыми значениями и вычисляется погрешность. Значение погрешности, а также градиента функции погрешности используют для коррекции весов, и действия повторяются. Процесс обучения прекращается если пройдено определенное количество эпох, или если погрешность достигает определенного уровня малости, или если погрешность перестает уменьшаться (пользователь преимущественно сам выбирает нужный критерий останова).

Градиентное обучение

Наиболее общим способом оптимизации нейросети является итерационная процедура подбора весов, называемая обучением, в данном случае - обучением с учителем, поскольку опирается на обучающую выборку примеров {x , d }, например - примеров правильной классификации.

Ошибка сети (целевая функция) формулируется, как правило, в виде квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов. В случае единичной обучающей выборки

(x, d) целевая функция определяется в виде:

1 M

E(wij ) 2 ( yk dk )2 (8.4)

k 1

Когда функция Е, выражающая ошибку, задана, задача сводится к такому «исправлению» весов wij, чтобы функция ошибки стала как можно меньше.

Для этого можно предложить, градиентную итерационную процедуру подбора матрицы весов w:

Выражение (8.7) является основной расчетной формулой для модификации синаптических весов сети при обучении. Здесь t w -

скорость обучения на шаге t. Можно показать, что, постепенно уменьшая

скорость обучения, например по закону t 1t , описанная выше процедура приводит к нахождению локального минимума ошибки Е.

Наибольшую трудность здесь вызывает процедура расчета градиента

функции ошибки E . Дело в том, что ошибка сети определяется по ее

wij

выходам, т.е. непосредственно связана лишь с выходным слоем весов.

Вопрос состоял в том, как определить ошибку для нейронов на скрытых

слоях, чтобы найти производные по соответствующим весам. Нужна была процедура передачи ошибки с выходного слоя к предшествующим слоям сети, в направлении обратном обработке входной информации. Поэтому такой метод, когда он был найден, получил название метода обратного распространения ошибки.

Метод обратного распространения ошибки

В случае дифференцируемых функций активации правило нахождения производных по любому весу сети дается т.н. цепным правилом дифференцирования.

Производная считается следующим образом. Рассмотрим сначала веса нейронов выходного слоя: обозначим j Out. Найдем производную функции ошибки по некоторому весу wij, соединяющему i-тый нейрон предпоследнего

слоя с j-тым нейроном последнего: E .

wij

Вес wij влияет на ошибку только в составе суммы: S j wij xi . Поэтому

i

Таким образом, невязка выходного слоя вычисляется по формуле:

и производная ошибки по любому весу выходного слоя вычисляется как:

Теперь рассмотрим нейрон j, находящийся не на последнем, а на некотором промежуточном, n-ном уровне. В этом случае у него есть выходы,

соединяющие его с нейронами следующего, (n+1) слоя. Тогда невязку [j n ]

можно записать как:

и невязка для j-того нейрона n-ного слоя найдется как:

k

Видно, что для определения невязки n-ного слоя необходимо знать невязку следующего, n+1 слоя.

Тогда производная функции ошибки Е по произвольному синаптическому весу wij[ n ] вычисляется по формуле: