ВОПРОСЫ_И_Лекции по КГ
.pdf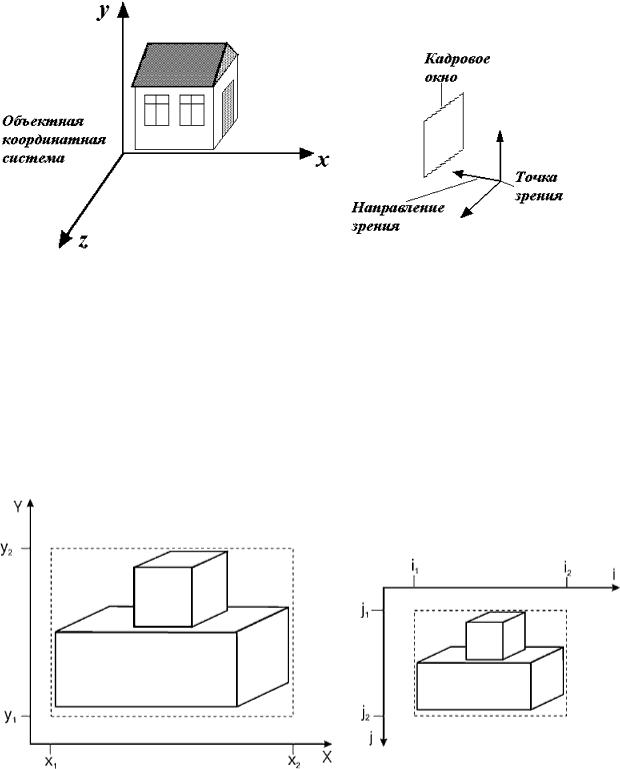
Рис. 4.3. Объектная система координат и система координат наблюдателя
Видимый образ формируется на некоторой плоскости, которую в дальнейшем будем называть картинной плоскостью. Способы преобразования трехмерного объекта в двумерный образ (проекции) могут быть различными. Так или иначе, но полученный образ также должен быть описан в некоторой двумерной системе координат . В зависимости от способа его получения реальные размеры образа также могут быть различны. Различные виды проецирования будут подробно рассмотрены позднее.
Рис. 4.4. Картинная плоскость и экран Поскольку нашей конечной целью является получение изображения на экране,
то перенесение образа сопровождается изменением масштаба в соответствии с размерами экрана. Обычно началом координат в системе координат образа считается левый нижний угол листа с изображением. На экране дисплея начало координат традиционно находится в левом верхнем углу. Отображение рисунка с картинной плоскости на экран должно производиться с минимальным искажением пропорций, что само по себе вносит ограничение на область экрана, занимаемую рисунком.
81
Изменение масштаба должно осуществляться с сохранением пропорций области (рис.
4.4).
Объекты в системе координат картинной плоскости задаются в какихлибо единицах измерения, причем масштаб одинаков по обеим осям координат. На экране единицей измерения является пиксель, который следует рассматривать как прямоугольный, поэтому масштабы по горизонтальной и вертикальной осям могут быть различны, что необходимо учитывать при задании коэффициентов масштабирования
Пример преобразований в системах координат
Для того, чтобы управлять изображением на экране, вносить изменения в его положение, ориентацию и размер производят геометрические преобразования. Они позволяют изменять характеристики объектов в пространстве. Допустим необходимо создать на компьютере изображение движения солнца по небу и автомобиля по земле. Данную картину наблюдатель видит из определенной точки в пространстве в определенном направлении. Чтобы описать эти сложные преобразования математически сначала следует выбрать системы координат.
Первая система координат – мировая, зададим ее осями xмyмzм, она размещается в некоторой точке и остается всегда неподвижной.
Вторая система координат определяет положение наблюдателя в пространстве и задает направление взгляда – система координат наблюдателя xnynzn.
Третья система – система координат объекта, их будет две: система координат солнца и система координат автомобиля. Эти системы могут перемещаться и изменять свое положение в пространстве относительно мировой системы координат. Координаты точек объектов задаются в системах координат объектов, каждая из них привязана к мировой системе координат. Система координат наблюдателя тоже перемещается относительно мировой системы координат. Чтобы увидеть трехмерный объект на дисплее нужно выполнить:
Преобразовать координаты объекта, заданные в собственной системе координат, в мировые координаты;
Преобразовать координаты объекта из мировой системы в систему
координат наблюдателя; Спроецировать полученные координаты на плоскость в с системе координат
наблюдателя, при этом мы будем иметь положение всех объектов сцены в координатах сцены.
Этапы построения изображений
Как было сказано ранее, компьютерная графика изучает методы построения изображений различных геометрических объектов и сцен. Главными этапами построения изображений являются:
Моделирование, которое использует методы математического описания объектов и сцен самой разной природы в двух- и трехмерном пространстве.
82
Визуализация – методы построения реалистических изображений объемного мира на плоском экране дисплея ЭВМ, при этом модели объектов и сцен преобразуются в статическое изображение или фильм
(последовательность статических кадров).
Все графические объекты приводятся к алгоритмическому виду, это отличает компьютерную графику от обычной.
Геометрические преобразования
Цель изучения геометрических преобразований – научиться описывать движение объектов и визуализировать объекты математически. Геометрическое преобразование – это отображение образа точки, принадлежащей n -мерному Евклидову пространству в точку n’ -мерного прообраза. К геометрическим преобразованиям относятся проективные преобразования и аффинные преобразования.
Проективные преобразования. Проекции
Для того чтобы синтезировать изображение на экране ПК, необходимо предложить способ математического описания объектов в трехмерном пространстве или на плоскости. Проективные преобразования изображают сцену в желаемом ракурсе. Проекцией называется способ перехода трехмерных объектов к их изображению на плоскости. Проецирование – это отображение трехмерного пространства на двухмерную картинную плоскость (КП). Получение проекции основывается на методе трассировки лучей. Из центра проецирования (проектора) проводятся лучи через каждую точку объекта до пересечения с КП. Фигура на плоскости, которая образуется точками пересечения лучей с картинной плоскостью, является проекцией объекта. Важным свойством любого метода проецирования является достоверность восприятия объекта по его проекции. Проекции, одинаково хорошо подходящей для любых задач не существует. Плоская геометрическая проекция – это тип проецирования на плоскую поверхность прямыми линиями. Плоские геометрические проекции бывают центральные и параллельные. Если центр проекции находится на конечном расстоянии от проекционной плоскости, то это центральная проекция. Если центр проекции удален на бесконечность, то такая проекция является параллельной. Центральные проекции имеют от одной до трех точек схода. Точкой схода называется точка пересечения центральных проекций всех параллельных прямых, которые не параллельны проекционной плоскости.
Итак, центральные проекции бывают с разным количеством точек схода. Параллельные проекции имеют много типов, но основными можно считать ортогональные и косоугольные.
Простейшей проекцией является параллельная прямоугольная проекция. В ней совместно изображаются виды сверху, спереди и сбоку.
83
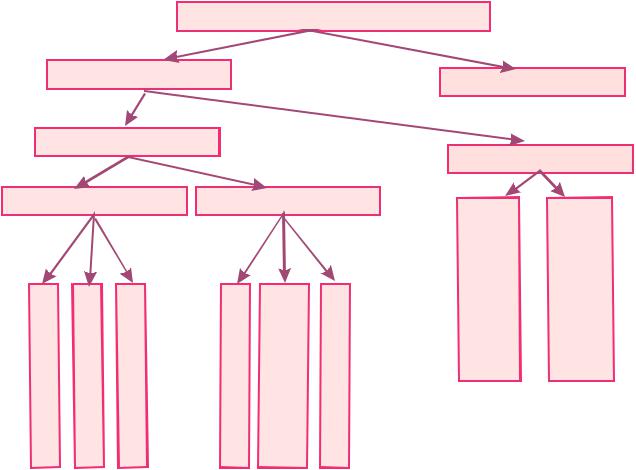
Проекции
Параллельные
Прямоугольные
Ортографические Аксонометрические
Видспереди |
сверху |
сбоку |
Изометрическая |
Прямоугольная диметрическая |
Триметрическая |
|
Вид |
Вид |
|
|
|
|
|
|
|
|
Центральные
Косоугольные
Косоугольная |
диметрическая |
Косоугольная |
изометрическая |
Основные виды проекций
Параллельные проекции
Параллельные проекции разделяются на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости. Если эти направления совпадают, т.е. направление проецирования является нормалью к проекционной плоскости, то проекция называется ортографической. Если же проекторы не ортогональны к проекционной плоскости, то проекция называется
косоугольной.
84
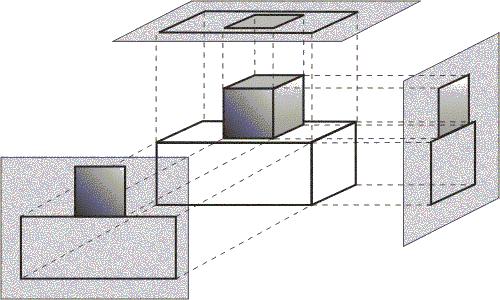
Рис. 7.3. Ортографические проекции
Винженерной графике наиболее широко используемыми видами ортографических проекций являются вид спереди, вид сверху (план) и вид сбоку, в которых проекционная плоскость перпендикулярна главным координатным осям, совпадающим вследствие этого с направлением проецирования (рис. 7.3). Поскольку каждая проекция отображает лишь одну сторону объекта, часто совсем непросто представить себе пространственную структуру проецируемого объекта, даже если рассматривать сразу несколько проекций одного и того же объекта. Но тем не менее такие чертежи позволяют определять реальные размеры объекта.
Вслучае аксонометрических ортографических проекций используются проекционные плоскости, не перпендикулярные главным координатным осям, поэтому на них изображается сразу несколько сторон объекта, так же как и при центральном проецировании, однако в аксонометрии укорачивание постоянно, тогда как в случае центральной проекции оно связано с расстоянием от центра проекции. При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояния же можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами).
85
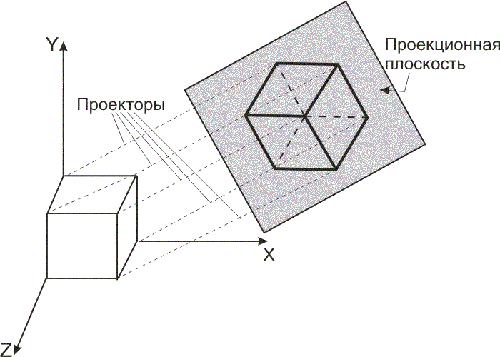
Рис. 7.4. Изометрическая проекция Аксонометрические проекции подразделяются на три группы в соответствии с
расположением проекционной плоскости по отношению к осям координат. Если нормаль к проекционной плоскости образует три различных угла с осями, то проекция называется триметрической (триметрией). Если два из этих углов одинаковы, то получаем диметрическую проекцию (диметрию). И, наконец, если все три угла равны между собой, то проекция называется изометрической (изометрией). Изометрическая проекция обладает тем свойством, что все три главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом (отсюда название: "изо", что означает "равно", и "метрия" - "измерение"). Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом (рис. 7.4).
Косоугольные проекции также являются параллельными, причем проекционная плоскость перпендикулярна главной координатной оси. Сторона объекта, параллельная этой плоскости, проецируется так, что можно измерять углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Мы коснемся только двух наиболее часто используемых косоугольных проекций: проекции кавалье (cavalier) и кабине (cabinet). В отечественной практике эти проекции называют горизонтальной косоугольной изометрией и кабинетной проекцией.
86
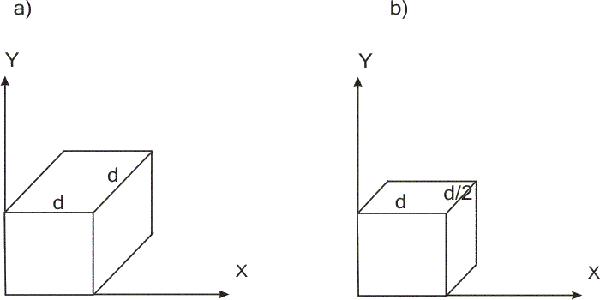
Рис. 7.5. Горизонтальная косоугольная изометрия (а) и кабинетная проекция (б)
В проекции горизонтальной косоугольной изометрии направление проецирования составляет с плоскостью угол 45°. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т.е. укорачивание отсутствует Кабинетная проекция имеет направление
проецирования, которое составляет с проекционной плоскостью угол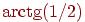 
. При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют 1/2 их действительной длины, что более соответствует нашему визуальному опыту, поэтому изображение выглядит более реалистично (рис. 7.5b).
Центральные проекции
Когда пучок проекторов исходит из заданного центра проекции, то параллельные отрезки на плоскости проекции уже не будут параллельными, за исключением случая, когда они лежат в плоскости, параллельной проекционной. При проецировании нескольких параллельных прямых их проекции пересекаются в так называемой точке схода. Если совокупность прямых параллельна одной из координатных осей, то их точка схода называется главной. Таких точек может быть не больше трех. Например, если проекционная плоскость перпендикулярна оси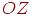 
, то лишь на этой оси будет лежать главная точка схода, поскольку прямые, параллельные как оси 
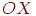, так и 
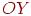, параллельны также и проекционной плоскости и поэтому не имеют точки схода.
Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно, и от числа координатных осей, которые пересекает проекционная плоскость. На рис. 7.6 приведены три различные одноточечные проекции куба, причем две из них имеют одну точку схода, а третья - две точки.
87
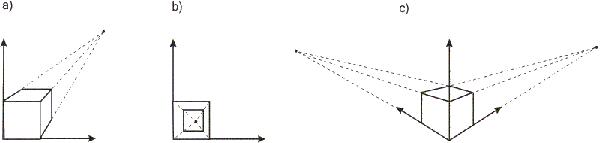
Рис. 7.6. Одноточечные и двухточечная проекции Двухточечная центральная проекция широко применяется в архитектурном,
инженерном и промышленном проектировании и в рекламных изображениях, в которых вертикальные прямые проецируются как параллельные и, следовательно, не сходятся. Трехточечные центральные проекции почти совсем не используются, вопервых, потому, что их трудно конструировать, а вовторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией.
Проективные преобразования могут применяться для быстрого построения:
различных фигур и изображений на плоских и криволинейных поверхностях;
сцен от первого лица, изображаемых с позиций подвижного наблюдателя;
простейших оптических эффектов – теней, отражений, преломлений. Основное преимущество проективных алгоритмов – возможность группового
преобразования точек , т. е. параллельных вычислений по одним и тем же формулам для всего множества точек. Этот подход к организации вычислительного процесса составляет конкуренцию алгоритмам трассировки, в которых проводятся индивидуальные лучи через каждую точку каждого объекта. Процесс трассировки более трудоемок и имеет преимущество только при малом числе точек и высокой сложности их преобразования.
Аффинные преобразования
Аффинное преобразование имеет следующие свойства:
отображает n-мерный объект в n-мерный – точку в точку, линию в линию, поверхность в поверхность;
сохраняет параллельность линий и плоскостей;
сохраняет пропорции параллельных объектов – длин отрезков на параллельных прямых и площадей на параллельных плоскостях.
Эти свойства позволяют строить прообразы полигонов на плоскости и полиэдров в пространстве по конечному набору m точек их вершин. К элементарным аффинным преобразованиям относятся перенос, масштабирование, сдвиг, вращение. При преобразовании сдвига происходит переписывание части изображения, при сдвиге могут производиться операции над кодами пикселов, например, старый пиксел может заменяться на новый или в видеопамять может заноситься результат операции исключающее ИЛИ над старым и новым кодами пикселов. При масштабирование коэффициент масштабирования может быть целым и дробным.
88
Сложным аффинным преобразование называется преобразование, реализующее цепочку не менее, чем из двух элементарных преобразований. Почти все аффинные преобразования не коммутативны, т. е. результат цепочки преобразований зависит от порядка их выполнения. Аффинные преобразования – основа кинематического метода построения параметрических объектов (кривых и поверхностей). Этот метод генерирует состояние объекта из заданных начальных состояний точки, отрезка, окружности как функции некоторого параметра, имеющего физический смысл времени движения. Конечным результатом преобразований являются не уравнения объекта, а его изображение на экране.
Двумерные геометрические преобразования
При формировании изображения постоянно возникает необходимость его изменять. При этом используются команды редактирования: перемещение, масштабирование, поворот, копирование, осевая симметрия и другие. В основе изменения графической информации лежат три элементарных аффинных преобразования: перенос, масштабирование и поворот.
Перенос
Точки на плоскости можно перенести в новые позиции, если добавить к координатам этих точек константы переноса. Пусть точка P(x,y) перемещается в
новую точку P′(x′,y′), при этом по оси x она сдвигается на Dx , а по оси y на величину Dy. Тогда имеем:
x′=x+Dx, =y+Dy
Определим векторы строки:
P=[xy] P′=[x′y′] T=[DxDy]
Получим уравнение
[x′y′]=[xy]+[DxDy] или сокращенно P′=P+T
Однако объект состоит из множества точек и необходимо для переноса объекта применить уравнение переноса для каждой точки. Удобнее переносить две крайние точки отрезка, а затем вычерчивать новый отрезок между ними.
89
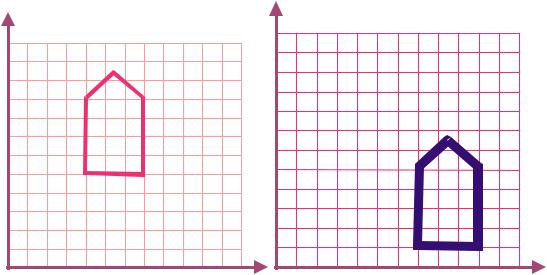
Рис. Перенос объекта Dx=3, Dy=-4
(4,5) (7,5)
(7,1) (10,1)
Масштабирование
Точки можно масштабировать (растягивать) по оси x в Sx раз и по оси y в Sy раз. Новые точки получаются с помощью умножения:
x′=x*Sx y′ =y*Sy
Определяем S в виде матрицы :
S |
|
Sx |
0 |
|
|
0 |
Sy |
||
|
Получим новые точки в матричном виде:
x' y' xy * |
Sx |
0 |
или P′=P*S |
|
|
|
0 |
|
|
|
|
Sy |
|
|
Масштабирование производится относительно начала координат. Если масштабирующие коэффициенты меньше единицы, то домик уменьшится и станет ближе к началу координат. Если масштабирующие коэффициенты больше единицы, то домик увеличится и отдалится от начала координат. Если Sx≠Sy, то это неоднородное масштабирование, и пропорции домика изменяются. Однородное масштабирование Sx=Sy, не влияет на пропорции.
Масштабирование объекта Sx=1/2, Sy=1/4
90