
u_lectures
.pdf3
Федеральное агентство по образованию Федеральное государственное образовательное учреждение
высшего профессионального образования «Сибирский федеральный университет»
А. П. Смольников
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Конспект лекций
4
Красноярск 2007
ОГЛАВЛЕНИЕ |
|
|
|
МОДУЛЬ 1. ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕКОГО |
3 |
УПРАВЛЕНИЯ |
|
Раздел 1. Анализ и синтез линейных систем автоматического |
3 |
управления |
|
1. Общие сведения |
3 |
1.1. История развития автоматики и ТАУ |
4 |
1.2. Основные понятия и определения о системе |
5 |
автоматического регулирования |
|
1.3. Классификация САУ. Системы стабилизации |
7 |
1.4. Основныепринципырегулирования |
9 |
1.5. Понятие о линейных и нелинейных системах |
12 |
2. Методы линеаризации систем автоматического управления |
14 |
2.1. Линеаризация статических характеристик звеньев |
14 |
2.2. Линеаризация нелинейных дифференциальных уравнений |
15 |
2.3. Безразмерная форма записи уравнений |
16 |
3. Характеристики динамических звеньев системы |
18 |
3.1. Передаточная функция звена |
18 |
3.2. Временные характеристики динамических звеньев |
19 |
3.3. Частотные характеристики звеньев |
22 |
3.3.1. Амплитуднофазовая частотная характеристика |
24 |
3.3.2. Логарифмические частотные характеристики |
24 |
3.4. Понятие об устойчивых и минимально-фазовых звеньях |
27 |
4. Типовые динамические звенья |
29 |
4.1. Безынерционное или пропорциональное звено. |
29 |
4.2. Апериодическое звено первого порядка |
31 |
4.3. Звено второго порядка |
34 |
4.3.1. Колебательное звено |
35 |
4.3.2. Апериодическое звено второго порядка |
39 |
4.4. Интегрирующие звенья |
41 |
4.4.1. Идеальное интегрирующее звено |
41 |
4.4.2. Интегрирующее звено с замедлением |
43 |
4.4.3. Пропорционально-интегральное звено |
45 |
4.5. Дифференцирующие звенья |
46 |
4.5.1. Идеальное дифференцирующее звено |
46 |
5
4.5.2. Дифференцирующее звено с замедлением |
48 |
||||
5.Структурные схемы систем автоматического управления |
51 |
||||
5.1 Элементы структурных схем |
|
|
51 |
||
5.2.Типовые соединения звеньев |
|
52 |
|||
5.3.Правила преобразования структурных схем |
53 |
||||
5.4. Теорема Мейсона |
|
|
|
57 |
|
5.5. Типовые передаточные функции САУ |
|
58 |
|||
6. Устойчивость линейных САУ |
|
|
60 |
||
6.1. Понятие об устойчивости. Теоремы Ляпунова. |
60 |
||||
6.2. Критерии устойчивости |
|
|
62 |
||
6.2.1. Критерий устойчивости Рауса |
|
62 |
|||
6.2.2. Критерий Гурвица |
|
|
63 |
||
6.2.3. Критерий Михайлова |
|
|
64 |
||
6.2.4. Критерий устойчивости Найквиста |
|
66 |
|||
6.2.5. Анализ устойчивости САУ по логарифмическим |
|
||||
частотным |
|
|
|
|
|
|
характеристикам |
|
|
69 |
|
7. Расчет переходных процессов САУ |
|
71 |
|||
7.1. |
Операторный |
метод |
решения |
дифференциальных |
71 |
уравнений |
|
|
|
|
|
7.2. Частотный метод расчета переходных процессов |
72 |
||||
8. Качество процессов регулирования |
|
73 |
|||
8.1. Оценка качества по переходной функции |
73 |
||||
8.2. Косвенные методы оценки качества |
|
74 |
|||
9. Синтез систем регулирования |
|
|
77 |
||
9.1. Выбор последовательных корректирующих устройств |
77 |
||||
9.2. Выбор параллельных корректирующих устройств в виде |
79 |
||||
обратных связей |
|
|
|
|
|
9.3. Построение желаемой ЛАЧХ скорректированной системы |
82 |
||||
9.4. Корректирующие звенья. Их типы и реализация |
86 |
||||
9.4.1. Пассивные четырехполюсники |
|
86 |
|||
9.4.2. Реализация сложных корректирующих звеньев |
88 |
||||
9.4.3. Активные четырехполюсники постоянного тока |
89 |
||||
10. Повышение точности САУ |
|
|
92 |
||
10.1. |
Увеличение |
коэффициента усиления разомкнутой |
92 |
||
системы |
|
|
|
|
|
10.2. Коэффициенты ошибок |
|
|
94 |
||
10.3. Повышение степени астатизма |
|
96 |
|||
Раздел 2. Математическое описание и синтез САУ в |
|
||||
пространстве состояний |
|
|
|
||
11. Математическое описание САУ в пространстве состояний |
98 |
||||
6
11.1. Описание САУ в виде уравнений пространства состояний |
98 |
|||
11.2. Запись уравнений состояния по структурной схеме |
99 |
|||
11.3. Составление уравнений состояния по известной |
102 |
|||
передаточной функции |
|
|
|
|
11.4. Основные соотношения для уравнений состояния |
105 |
|||
12. Синтез модальных регуляторов |
|
108 |
||
13.Управляемость и наблюдаемость САУ |
|
113 |
||
13.1. Управляемость САУ |
|
|
113 |
|
13.2. Наблюдаемость САУ |
|
|
114 |
|
14.Идентификация вектора состояния системы |
|
115 |
||
14.1. Принципы построения наблюдающего устройства полного |
115 |
|||
порядка. |
|
|
|
|
14.2. Редуцированный наблюдатель |
|
119 |
||
15.Особенности динамики системы, замкнутой через наблюдатель |
124 |
|||
|
|
|
|
|
МОДУЛЬ |
2. |
ДИСКРЕТНЫЕ |
СИСТЕМЫ |
126 |
АВТОМАТИЧЕКОГО УПРАВЛЕНИЯ |
|
|
||
Раздел 3. Линейные импульсные системы |
|
126 |
||
16. Математическое описание импульсных систем |
|
126 |
||
16.1. Определение линейных импульсных систем |
|
126 |
||
16.2. Виды модуляции сигналов |
|
128 |
||
16.2.1. Общее понятие амплитудной модуляции сигналов |
128 |
|||
16.2.2. ИЗ с амплитудной и широтной модуляцией |
129 |
|||
16.3. Эквивалентная схема импульсной системы |
|
131 |
||
16.4. Применение преобразований Фурье и Лапласа для |
134 |
|||
дискретных сигналов |
|
|
|
|
17. Особенности спектров дискретных сигналов |
|
136 |
||
17.1. Связь между частотными спектрами непрерывных и |
136 |
|||
дискретных величин |
|
|
|
|
17.2. Прохождение сигналов через импульсную САУ |
138 |
|||
17.3. Прохождение сигналов через ИСАУ при выполнении |
|
|||
условий |
|
|
|
|
теоремы Котельникова |
|
|
139 |
|
18. Передаточные функции импульсных систем |
|
141 |
||
18.1. Передаточная функция и частотная передаточная |
|
|||
функция |
|
|
|
|
разомкнутой импульсной системы |
|
141 |
||
18.2. Определение передаточной функции разомкнутой системы |
|
|||
по передаточной функции непрерывной части |
|
143 |
||
18.3. Передаточные функции замкнутых систем |
|
147 |
||
19.Устойчивость импульсных систем автоматического управления |
151 |
|||
7
19.1. Понятие об устойчивости |
|
|
|
151 |
|||
19.2.Критерий устойчивости Гурвица для импульсных систем |
152 |
||||||
19.3.Критерий устойчивости Михайлова для импульсных систем |
152 |
||||||
19.4.Критерий устойчивости Найквиста для импульсных систем |
154 |
||||||
20. Коррекция импульсных систем |
|
|
|
155 |
|||
20.1. Способы коррекции |
|
|
|
|
155 |
||
20.2.Условия конечной длительности переходного процесса |
156 |
||||||
21. Расчет переходных процессов импульсных САУ |
|
|
158 |
||||
22. Применение ЛЧХ для импульсных САУ |
|
|
|
162 |
|||
22.1. ЛЧХ импульсных САУ |
|
|
|
162 |
|||
22.2. Методика построения ЛЧХ |
|
|
|
163 |
|||
22.3. Синтез ИСАУ методом ЛЧХ |
|
|
|
166 |
|||
Раздел 4. Цифровые САУ с микро-ЭВМ |
|
|
|
168 |
|||
23. Математическое описание цифровых САУ |
|
|
168 |
||||
23.1. Функциональная схема цифровой САУ |
|
|
168 |
||||
23.2. Особенности цифровых САУ |
|
|
|
169 |
|||
23.3. Преобразование данных и квантование по уровню |
|
171 |
|||||
23.4. Линеаризация статических характеристик АЦП и ЦАП |
174 |
||||||
23.5. Структурная схема и передаточная функция цифровой САУ |
175 |
||||||
23.6. Передаточные функции цифровой САУ |
|
|
177 |
||||
23.7. Приближенное определение дискретной передаточной |
|
||||||
функции |
|
|
|
|
|
|
|
по |
передаточной |
функции |
непрерывной |
части |
178 |
||
(подстановочный метод) |
|
|
|
|
|
||
24. Реализация на микроЭВМ цифровых алгоритмов управления |
182 |
||||||
24.1. Дифференцирование цифровых последовательностей |
|
182 |
|||||
24.2. Цифровые интеграторы |
|
|
|
183 |
|||
24.3.Обобщенная формула численного интегрирования. |
185 |
||||||
Компенсация |
|
ошибок |
|
|
|
|
|
24.4. Дискретные регуляторы |
|
|
|
186 |
|||
24.5. Выбор параметров цифрового регулятора |
|
|
188 |
||||
25. Техническая реализация цифровых САУ |
|
|
|
190 |
|||
|
|
|
|
|
|
||
МОДУЛЬ |
3. |
|
НЕЛИНЕЙНЫЕ |
СИСТЕМЫ |
194 |
||
АВТОМАТИЧЕКОГО УПРАВЛЕНИЯ |
|
|
|
|
|||
Раздел 5. Нелинейные системы управления |
|
|
194 |
||||
26. Математическое описание нелинейных САУ |
|
|
194 |
||||
26.1. Особенности нелинейных систем управления |
|
|
194 |
||||
26.2. Общие характеристики НЗ |
|
|
|
195 |
|||
26.3. Типовые |
нелинейные звенья |
с |
однозначными |
196 |
|||
характеристиками |
|
|
|
|
|
|
|
8
26.4. Звенья с неоднозначными характеристиками |
197 |
|
26.5. Основные виды соединений нелинейных звеньев |
198 |
|
26.6. Способы нейтрализации нелинейных звеньев |
199 |
|
27. Приближенные методы исследования на основе метода |
202 |
|
гармонической |
линеаризации нелинейностей |
|
27.1. Метод гармонической линеаризации нелинейностей |
202 |
|
27.2. Коэффициенты гармонической линеаризации релейных |
205 |
|
звеньев |
|
|
27.3. Метод гармонического баланса |
207 |
|
27.4. Условие гармонического баланса |
208 |
|
27.5. Графоаналитический метод определения параметров |
209 |
|
автоколебательного режима и его устойчивости |
|
|
28. Метод Ляпунова |
|
213 |
28.1. Понятие о знакоопределенных, знакопостоянных и |
213 |
|
знакопеременных |
функциях. |
|
28.2. Функция Ляпунова и её производная по времени |
213 |
|
28.3.Формулировка теоремы Ляпунова в векторно-матричной |
216 |
|
форме |
|
|
29.Условия абсолютной устойчивости нелинейных систем |
218 |
|
29.1. Понятие абсолютной устойчивости |
218 |
|
29.2.Частотный критерий абсолютной устойчивости В.М. |
218 |
|
Попова |
|
|
9
МОДУЛЬ 1. ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕКОГО УПРАВЛЕНИЯ
РАЗДЕЛ 1. АНАЛИЗ И СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
1. ОБЩИЕ СВЕДЕНИЯ
Развитие техники автоматического управления связано с проблемой замены человека в различных звеньях управления технологическими процессами.
В настоящее время вопросам автоматизации уделяется исключительно большое внимание, так как необходимость широкой автоматизации – это потребность самой практики.
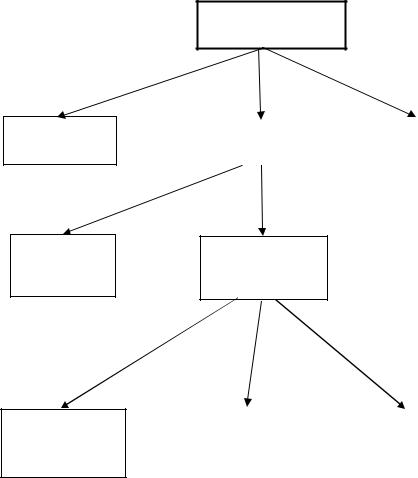
Сейчас используется несколько терминов для обозначения наук, изучающих вопросы автоматизации, их взаимосвязь представлена на рис. 1.1.
Экономическ
ая
Теория
информаци
и
Теория
автоматическо
го
Кибернетика
Техническая |
|
Медицинска |
кибернетика |
|
я |
|
|
|
Теория
автоматическог о управления
Теория |
|
Теория |
оптимальног |
|
адаптивных |
о управления |
|
систем |
|
|
|
Рис. 1.1
10
Кибернетика – наука об общих закономерностях процессов управления
– основывается на изучении объектов управления, получении информации о протекании процессов в объектах и выработке управляющих воздействии.
Причем объекты управления могут быть самые разные: биологические системы, предприятия, машины и их отдельные системы.
Техническая кибернетика – наука, рассматривающая управление техническими системами. Она включает в себя теорию информации и теорию автоматического управления.
Термины “управление” и “регулирование” часто используют как синонимы, однако они имеют различие.
Автоматическое регулирование – это поддержание постоянной или изменяющейся по заданному закону некоторой величины, характеризующей процесс, и осуществляется оно путем измерения состояния объекта и воздействия на регулирующий орган объекта.
Автоматическое управление – это воздействие на объект управления с целью достижения заданной цели управления, то есть охватывает более широкий круг задач. Под автоматическим управлением понимается автоматическое осуществление совокупности воздействий, выбранных из множества возможных на основании определенной информации и направленных на обеспечение функционирования объекта в соответствии с целью управления.
То есть задачи управления включают в себя задачи регулирования и, кроме того, вопросы самонастройки систем управления, оптимального управления и другие.
ТАУ – это наука о принципах построения и методах расчета систем автоматического управления. Ее выводы справедливы для различных систем независимо от назначения и физической природы. Применение систем их проектирование и эксплуатация невозможны без знания ТАУ.
1.1. История развития автоматики и ТАУ
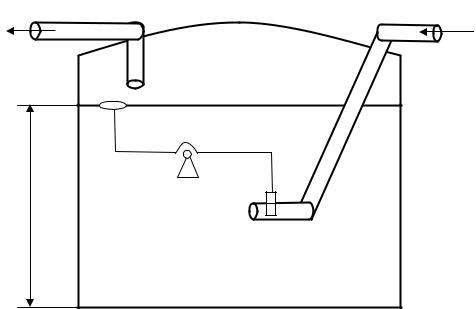
Первый автоматический регулятор был изобретен в 1765 г. И.И.Ползуновым (рис. 1.2). Он был предназначен для стабилизации уровня воды в котле паровой машины.
В 1768 г. разработан центробежный регулятор скорости вращения паровой машины Д. Уатта. Основоположник теории автоматического регулирования – И.А. Вышнеградский. В 1876 г. опубликована его работа “Регуляторы прямого действия”, в которой, он впервые получил условия устойчивости систем регулирования.
Большой вклад в развитие теории автоматического управления внесли российские ученые: Н.Е. Жуковский, А. Н. Чебышев, В.И. Столетов.
|
11 |
|
Па |
Питани |
|
е водой |
||
|
H
Рис. 1.2
После 1940 г. ТАР выделилась в самостоятельную науку. Были созданы методы расчета динамических систем.
В 50-х годах возникли новые направления: -теория оптимальных систем; -теория адаптивных систем.
Большой вклад внесли также советские ученые: Солодовников В.В., Петров Б.Н., Теодорчик К.Ф.. ТАУ развивается и в настоящее время.
1.2. Основные понятия и определения о системе автоматического регулирования
Протекание производственных процессов характеризуется переменными величинами t, V, P, которые называются параметрами производственных процессов. Чтобы производственные процессы протекали с высоким к.п.д. и заданной производительностью, необходимо параметры поддерживать на заданном уровне или изменять по определенному закону.
Объект регулирования – это установка, где регулируется какой – либо процесс.
Параметр, который поддерживается на определенном уровне или закономерно изменяется – называется регулируемым.
Величины, отражающие внешние влияния на объект, называются
воздействиями. Делятся на возмущающие воздействия и управляющие,
вырабатываемые человеком или управляющим устройством. Существует понятие заданного значения регулируемой величины.
12
Измеренное значение регулируемой величины в данный момент времени называется текущим значением регулируемой величины.
Разность между заданным и текущим значением называется ошибкой регулирования.
Автоматический регулятор – устройство, которое на основе ошибки регулирования вычисляет управляющее воздействие.
Устройство, предназначенное для перемещения регулирующего органа, называется исполнительным механизмом.
Регулирующий орган – устройство, предназначенное для воздействия непосредственно на параметры объекта.
Устройство для измерения регулируемой величины называется
чувствительным элементом (термопара).
Системой автоматического регулирования называется замкнутая динамическая система, состоящая из объекта регулирования и автоматического регулятора.
