26

Лекция 1 Приближённые методы решения слау

А) Метод простых итераций. (Метод последовательных приближений).

Пусть дана система n линейных уравнений с n неизвестными:

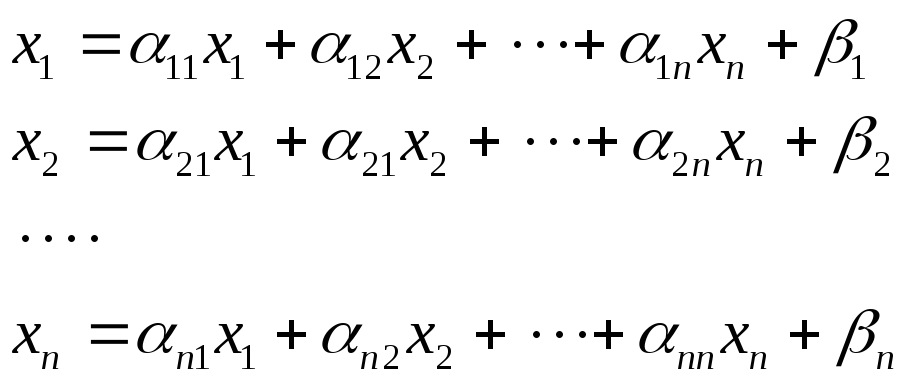(1)

или где- заданные числа;.

Задаются произвольно n-чисел – нулевое приближение искомой функции.

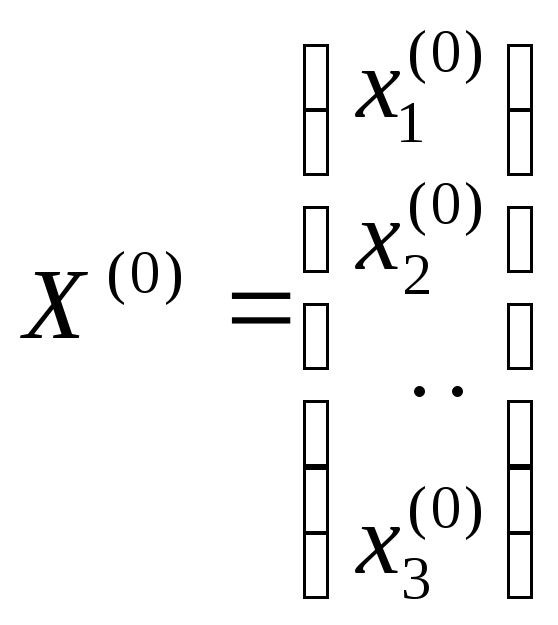
Далее подставляем в правую часть системы (1) нулевое приближение и

находим первое приближение.

, (2)

Затем по 1-ому приближению находят 2-ое, 3-е и т.д.

В результате для k-ого приближения получаем формулу:

, (2’)

Таким образом мы получили последовательность векторов

Х⁽⁰⁾,Х⁽¹⁾,…, Х^(К), к=1,2,…

Если любая из таких последовательностей {Х_i^(к)} сходится некоторому пределу x_i^k = c_i ,,то данный вектор с_i, является решением сист. (1)

В равенстве (2’) перейдем к пределу при k→∞ при замене х_i на с_i.

Теорема (достаточные условия сходимости простой итерации):

Пусть выполняется хотя бы одно из следующих условий (нормы матрицы):

а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1:

б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1:

в) Если сумма всех элементов в квадрате меньше 1.

Если выполняется хотя бы одно, тогда справедливы утверждения:

1. система (1) имеет единственное решение (С₁,... С_n);

2. последовательность , гдеi = определяется по формуле (2), при любом начальном приближении сходится к соответствующим компонентам точного решения.i =

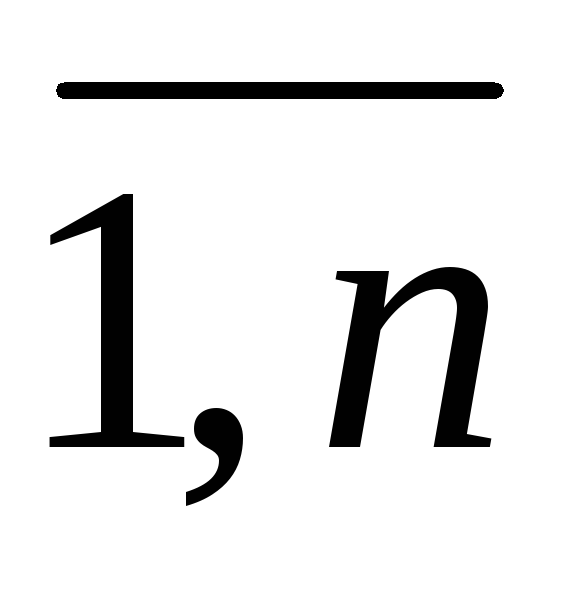
3. для приближенного равенства верны оценки (x₁^(k),…x_n^(k))(C_1,…C_n),

а’) если выполняется условие а), то

,

б’) если выполняется условие б), то

,

в’) если выполняется условие в), то

.

Замечания:

1)Если нет никакой информации о точном решении СЛАУ, то за начальное приближение выбираем столбец свободных коэффициентов. (из приведенной матрицы);

2)остановка вычислений производной по заданной величине абсолютной погрешности и приведенным в теореме оценкам.

Б) Метод Зейделя.

Этот метод является модификацией МПИ и заключается в том, что при вычислении (к+1) приближения неизвестного х_i (i>1), используются уже вычисленные ранее (к+1) приближения неизвестных х₁, х₂,…, х_i-1

Рассмотрим систему: i=1,n

Пусть матрица α удовлетворяет одному из условий теоремы:

Если, а) <1 (коэффициенты по строкам)

б) <1 (коэффициенты по столбцам)

в)<1 (все коэффициенты)

тогда общая формула метода Зейделя имеет вид:

к=1,2…

Замечание: метод Зейделя обычно, но не всегда сходится к точному решения быстрее, чем МПИ

В) Метод Гаусса. (Метод последовательного исключения переменных)

Матрица называется верхнетреугольной, если ниже главной диагонали все элементы равны нулю, т.е. a_ij=0 при i>j. Аналогично, матрица называется нижнетреугольной, если все элементы выше главной диагонали (i<j) равны 0. Матрица называется диагональной, если только на главной диагонали (i=j) стоят ненулевые элементы. Метод Гаусса решения систем линейных уравнений состоит из двух этапов: прямого хода и обратного хода.