страхование для выдачи студентам / Элементы страховой математики

Интеграл зависит от значения верхнего предела, поэтому исследуем 3

случая: 0 < x < 1; 1 < x < 2; 2 < x < 3. 2.1. 0 < x < 1; тогда:

a)если 0 < y < 1, то f2(y) = 12 ;

b)если 0 < x – y < 1, (т.е. x – 1 < y < x), то f1(x-y) = 1;

следовательно: f(x) = ∫x f1 (x − y) f2 (y) dy = ∫x 1 1/2 dy = x/2

2.2.1 < x < 2, тогда:

a)если 0 < y < 2, то f2(y) = ?;

b)если 1 < x – y < 2, то f1(x-y) = 0;

c)если 0 < x – y < 1, (т.е. x – 1 < y < x), то f1(x-y) = 1;

поэтому: f (x) = ∫x f1 f2 dy = x∫−1f1 f2 dy + ∫x f1 f2 dy;

В первом интеграле подынтегральная функция: 0 × f2 = 0, поэтому он обратится в 0, и останется только второй:

f (x) = ∫x f1 f2 dy = ∫x 1 1/ 2 dy =1/ 2

2.3.2 < x < 3, тогда:

a)при 0 < y < 2 имеем f2(y) = 12 ;

b)при 2 < y < 3 имеем f2(y) = 0.

f(x)=∫x f1 f2 dy=∫2 f1(x−y) 1/2 dy+∫x f1(x−y) 0 dy=1/2 ∫2 f1(x−y)dy

c) проанализируем f1(x – у) на (0;2).

Если 1 < x – у < 2, то f1(x – у) = 0;

Если 0 < x – у < 1, (т.е. x – 1 < y < x), то f1(x – у) = 1.

Поэтому:

f(x)=1/2 (x∫−1 f1(x−y)dy+ ∫2 f1(x−y)dy)=1/2 ∫2 1dy=(2−(x−1))/2=(3−x) / 2.

242

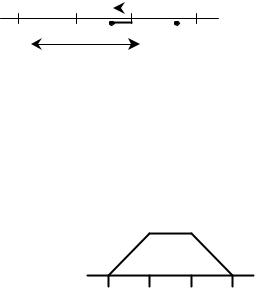
Замечание. Ситуацию на «2<x<3» проще проиллюстрировать рисунком (рис. 13.2.). Пересечение интервалов (0;2) и (х-1;х) образует отрезок: (х-1, 2).

x-1 x

Рис. 13.2.

Таким образом, вне интервала (0,3): f(x) = 0;

при 0 < x < 1: f(x) = x/2; при 1 < x < 2: f(x) = 12; при 2 < x < 3: f(x) = (3 – х)/2.

Таким образом, при U < 0:

g(U)= ∞∫f(x)dx = 1/4 +1/2 +1/4 = 1 .

u

Т.е. разорение наступает обязательно!

243

Очевидно, второй и третий интегралы сохранятся, а первый равен:

Поэтому: ∫3 f(x)dx = 1/4 −U2 /4 +1/2 +1/4 = 1 −U2 /4 ;

u

Итак: g(U) = 1 – U2/4.

3.3. 1 < U < 2;

∫3 = ∫2 + ∫3 = ∫2 1/2dx + 1/4 = (2 − U)/2 + 1/4 = 5/4 − U/2 ;

u u 2 u

Итак, g(U) = 5/4 – U/2.

3.4.2 < U < 3,

= 9/2 - 3/2 U - (9 - U2 ) / 4 = (3 −U )2 / 4 g(U) = (3 – U)2/4.

3.5. U > 3; g(U) = 0.

Получили 5 различных формул для g(U) в зависимости от U. Теперь для удобства составим таблицу.

Это позволяет составить выражение для R в каждом интервале U, используя pi, qi (первой ситуации соответствует вероятность 0,24, второй 0,14, третьей 0,06).

Если U>3, то вероятность разорения R = 0, это очевидно. Интересный эффект возникает при U < 0. С одной стороны, это

можно трактовать, как «долг», без средств для его погашения, поэтому вероятность разорения в этом случае R = 1; - неизбежное банкротство. Но, с другой стороны, нас интересует только разорение в результате страховой деятельности. И здесь играет роль не столько

244

отрицательный U, сколько возникновение требований об оплате, которые невозможно удовлетворить. А вероятность этого 0,44.

Тот же результат получается, если формально вычислить:

1 × 0,24 + 1 × 0,14 + 1 × 0,06 = 0,44.

Поэтому необходимо точно указывать, что именно понимается под разорением.

Рассмотрим остальные варианты.

4.1. 0 < U < 1;

R = (1 – U) × 0,24 + (1 – U/2) × 0,14 + (1 – 0,25 × U2) × 0,06 =

= 0,44 – 0,31U – 0,015U2

R(0) = 0,44, что обеспечивает непрерывность функции.

R(1) = 0,115.

Первая и вторая производные – отрицательны. Вероятность монотонно убывает с ростом капитала, причем, чем дальше, тем скорее (парабола с ветвями вниз).

4.2. 1<U<2

R = 0 × 0,24 + (1-U/2) × 0,14 + (5/4-U/2) × 0,06 = 0,215 – 0,1U.

R(1) = 0,115; R(2) = 0,015.

Функция продолжает монотонно убывать, но по прямой.

4.3. 2 < U < 3;

R = 0,06(3 – U)2 /4 = 0,135 – 0,09U + 0,015U2; R(2) = 0,015; R(3) = 0.

Функция непрерывна и продолжает убывать, но если первая производная отрицательна, то вторая – положительна. Т.е. функция достигла глобального минимума при U = 3. Это вполне согласуется со здравым смыслом. Если капитала достаточно для выплаты полного возмещения по всем договорам, то разорение невозможно.

В качестве упражнения рекомендуется построить график функции R(U). Для наглядности можно использовать переменный масштаб.

Так как функция монотонно убывает на всем отрезке (0,3), то каждому значению вероятности разорения R соответствует единственное значение U, обеспечивающее это R. Т.е. можно построить и обратную функцию зависимости U(R), (просто поменяв местами оси координат).

Замечание. При самоподготовке рекомендуется составить аналогичный пример, заменив значения Si,pi. Легко убедиться, что изменения в расчетах весьма незначительны. В частности, принципиальный вид графиков сохранится.

245

В реальных задачах, где число договоров существенно больше двух, аналитическое решение с использованием аппарата свертки, конечно, возможно, но на практике применяется численный расчет.

13.5.Суммарный ущерб в портфеле из двух договоров

Согласно теории вероятности, плотность распределения суммы двух независимых случайных величин определяется с помощью операции свертки:

H(z) = P{Z < z} = P{X + Y < z} = P{(X < x) (Y < z − x)} = ∫Z f(x) g(z − x)dx

0

В частности, можно показать, что если первая распределена произвольно, а вторая – равномерна на (a,b), то плотность суммы этих двух величин задается формулой:

p(z) = (F1(z-a) - F1(z-b))/(b-a)

Из этого следует, что для двух равномерных на (a,b) и (c,d) СВ справедливо: F1(x) = (x – c)/(d – c) , тогда:

F1(z-a) = (z-a-c)/(d-c) и F1(z-b) = (z-b-c)/(d-c);

∞

поэтому: p(z) = ∫ p1(x)p2(z-x)dx

−∞

Причем: a<x<b , c<z-x<d (т.е. z-d<x<z-c), следовательно:

max(a, z-d) < x < min (b, z-c). Т.е. интегрировать надо именно по этому отрезку. Поэтому искомая плотность равна:

(min (b, z-c) - max(a, z-d))/(b-a)(d-c).

Требуется конкретизировать числитель по значениям: a,b,c,d.

1)P(z) = (z-c-a)/(d-c)(b-a), при (z<b+c) и (z<a+d).

2)P(z) = 1/(b-a), при (z<b+c) и (z>a+d).

3)P(z) = 1/(d-c), при (z>b+c) и (z<a+d).

4)P(z) = (b+d-z)/(d-c)(b-a), при (z>b+c) и (z>a+d).

Очевидно, случаи 2) и 3) взаимно исключают друг друга, поэтому остается только три.

Рассмотрим пример полного страхования от пожара двух домов, со страховыми суммами: в 1 е.с.с. и 2 е.с.с. и равномерным распределением величины ущерба при пожаре. Страховые случаи – величины независимые.

(a,b)=(0,1); (c,d)=(0,2). Тогда:

p(z) = z/2 , если (z<1 и z<2), т.е. z<1. p(z) = 1/2 , если (z>1 и z<2), т.е. 1<z<2. p(z) = (3-z)/2 , если (z>1 и z>2), т.е. z>2.

Получены те же результаты, что и в приведенном примере. Однако сравнение двух способов показывает неоспоримые преимущества данного метода, основанного на свертке. Он более логичен, строго обоснован, исключает возможность что-либо «не заметить», проще в реализации, менее трудоемок. Преимущества данного подхода станут

246

еще более очевидны, если появится третий договор, который надо включить в портфель.

Поэтому именно так и решаются подобные реальные задачи. На практике из-за требований универсальности программы основаны на численных методах реализации свертки.

Замечание. Если появляется третья равномерная величина, то при ее добавлении к СВ, равной сумме двух первых, плотность вновь построенной СВ в зависимости от соотношения между длинами отрезков, на которых заданы эти три исходные СВ, будет иметь вид:

Понятно, что по мере увеличения количества СВ в исследуемой сумме форма графика будет приближаться к нормальной кривой, что является следствием Закона Больших Чисел и иллюстрирует его действие.

13.6.Сложные пуассоновские процессы

Предположим, что случайные величины Xi - независимы и одинаково распределены; что они не зависят от N(t) при любом неотрицательном t; что случайный процесс (N(t)) - пуассоновский с параметром λ.

Pr(N(t) = k) = е-λ*t (λ t)k / k!, k = 0, 1, 2, 3,...

Ранее показано, что случайная величина S(t) при каждом t имеет сложное распределение Пуассона с параметром λ×t. Тогда процесс (S(t)) - сложный пуассоновский процесс с параметром λ. Пусть P(x) -

пуассоновская функция распределения, общая для всех Xi. Размеры требований - положительны, поэтому P(0) = 0. За единицу времени собранные взносы должны превосходить выплаты: c > λ × M(Xi). Иначе (в терминах надбавки): c = (1 +Θ) × λ × M(Xi).

247

R

пост. распр.

экспон. распр.

θ

Рис. 13.5.

В кн. Карри /6/ показано, что для экспоненциального распределения неравенство Лундберга дает очень хорошее приближение к точному значению вероятности разорения, причем с ростом начальных активов точность повышается.

Можно показать, что неравенство (граница) не зависит от единицы измерения денег, что вероятность ф(U) не зависит от λ. (ф(U) определяется на бесконечном интервале времени, а параметр λ проявляет себя в конечный момент времени, когда происходит разорение; но параметр не влияет на вероятность разорения).

Для иллюстрации рассмотрим два риска. В первом общий размер выплат распределен по сложному пуассоновскому закону с λ = 1, а выплаты имеют экспоненциальное распределение со средним 10. С учетом надбавки взнос равен 1 × 10 × (1 + Θ).

Второй риск отличается лишь параметром λ = 0,5 и для него взнос вдвое меньше: 0,5 × 10 × (1 + Θ).

При исследовании процесса на бесконечном интервале времени можно первый риск оставить без изменения, а для второго ввести новую единицу времени ‘два года’. Тогда второй риск на этом промежутке времени будет иметь те же характеристики, что и первый на традиционном (1 год), Поэтому на бесконечном интервале оба эти риска имеют одинаковые вероятности разорения!

13.8.Дисперсия, как мера стабильности

При выборе формы перестрахования важную роль играет оценка платежеспособности цедента, которая может быть получена на основе вероятности разорения страховщика. Эта вероятность вычисляется с помощью построения доверительных интервалов для агрегированных убытков. А границы интервала зависят от дисперсии.

Полезно использовать и степень риска (СКО/МО).

Следующий подход основан на непосредственном использовании

дисперсии агрегированных убытков. При большом числе рисков фактическое распределение можно аппроксимировать нормальным, для

249

которого при заданном уровне безопасности (1 - ε) минимальный начальный рисковый резерв U пропорционален СКО.

Поэтому уменьшение дисперсии повышает безопасность. Следовательно, из нескольких возможных перестраховочных договоров, лучшим (с точки зрения платежеспособности) является тот, который обеспечивает минимальную дисперсию (при прочих равных).

Можно ожидать, что этот подход применим и при других законах распределения величины ущерба. Поэтому выбор оптимального перестраховочного договора сводится к минимизации дисперсии.

В некоторых случаях, когда применима нормальная аппроксимация, (или использование сложного распределения Пуассона), может быть получено аналитическое обоснование этого результата. Приведем некоторые результаты без доказательства.

Пусть страховщик ищет перестраховочную политику с минимальной дисперсией для удерживаемого бизнеса (риска), в предположении о фиксированных перестраховочных рисковых взносах (рисковая надбавка перестраховщика не учитывается, например, если она пропорциональна его рисковой премии).

Предполагается также, что перестрахование организовано так, что однозначно определяет распределение убытка цедента и соответственно, средний убыток. В этом случае можно показать /6/, что перестрахование "стоп - лосс", где убыток цедента ограничен уровнем собственного удержания М, обеспечивает минимальную дисперсию при правильном выборе М. (Выбор М рассмотрен ранее). В этом договоре цеденту остается максимальная часть собранных взносов и при этом минимизируется его перестраховочный рисковый взнос.

На практике взносы в договоре "стоп - лосс" имеют большие рисковые надбавки (и нагрузки на ведение дел), поскольку на перестрахование переданы редкие очень большие риски, что сильно повышает дисперсию, а в надбавке растут весовые коэффициенты при дисперсии и СКО.

Поэтому правильнее считать, что перестраховочный взнос состоит из рискового взноса и "нагрузочной" функции, которая, очевидно,

должна быть неубывающей.

Пусть цедент хочет сохранить неизменной дисперсию своего риска и определить форму договора с минимальной ценой перестрахования. В этом случае можно показать /6/, что результат достигается в квотном перестраховании. Причем коэффициент пропорциональности равен отношению СКО оставленного риска к СКО общего риска.

13.9.Взаимные услуги по перестрахованию

Рассмотрим две страховые компании, которые оказывают друг другу услуги по перестрахованию. Первая имеет портфель с общим

250