
страхование для выдачи студентам / Элементы страховой математики
.pdf
Прежде всего, это относится к соотношению (на практике) между стремлением к получению максимальной прибыли и готовностью к риску. Наличие конкуренции приводит к тому, что зазор между ценой страхования и ценой перестрахования постоянно сужается. Следовательно, передавая риск, страховщик одновременно передает перестраховщику и соответствующую прибыль (а не только часть собранных взносов). Если страховщик не будет рисковать, он ничего не заработает.
Тем не менее, данный пример достаточно поучителен. Нельзя отказываться от варианта решения задачи только потому, что он на первый взгляд представляется бесперспективным. Необходим тщательный просчет всех допустимых в принципе вариантов, так как различие между оптимальным вариантом и “просто хорошим” может быть достаточно велика.
9.3. Обсуждение проблемы выбора аппроксимации биномиального распределения нормальным законом и распределением Пуассона
Из теории вероятностей известно, что при большом числе испытаний биномиальное распределение можно аппроксимировать:
-либо нормальным законом, если вероятность не очень мала (p>0.1);
-либо законом Пуассона для редких событий (p < 0.01). Естественно, одновременно использовать обе аппроксимации нельзя, кроме того, не вполне ясно, как быть, если 0.01< p < 0.1.
Феллер /27./ утверждает, что при достаточно большой
интенсивности потока Пуассона (λ > 20) это распределение можно успешно аппроксимировать нормальным законом. Проверим, как работает подобный прием для меньших значений интенсивности.
Пример 10. В предыдущем разделе приведен «комплексный пример», где n = 1000, p = 0.01, тогда λ= 10, и рассчитаны: P(k) и P(0<k<m).
Например, P(0<k<10)=0.583, P(0<k<14)=0.917, P(0<k<15)=0.951, P(0<k<18)=0.993, P(0<k<21)=0.9993.
Воспользуемся формулой: P(k<m/λ)=Ф((m+0.5-λ)/  λ ) и получим результаты:
λ ) и получим результаты:
P(k<14)=Ф(1.43)=0.844; P(k<15)=Ф(1.74)=0.918; P(k<18)=Ф(2.69)=0.993; P(k<21)=Ф(3.64)=0.9997.
Сравнение результатов показывает хорошее совпадение только вблизи «практической достоверности», а по мере удаления надежности от этого значения погрешность растет. На практике задача решается в обратном направлении, т.е. задается надежность и по ней определяется, сколько страховых случаев надо обеспечить. На основании этого рассчитывается надбавка и резерв, а также обосновывается выбор
161
перестраховочной программы. Поэтому необходимо соблюдать осторожность при подобной процедуре. Проиллюстрируем это.
При рассмотрении поведения страховщика на рынке
применялась нормальная аппроксимация биномиального распределения, так как вероятность наступления страхового случая р = 0.1 >> 0. Однако, часто значение р значительно ближе к 0, например, 0.01, тогда нормальная аппроксимация некорректна. Необходима аппроксимация Пуассоновским законом. Соответственно, изменится методика исследования. Рассмотрим пример.
Пример 11. Пусть n = 400, p = 0.01, S = C = 2000. При наступлении страхового случая выплачивается страховая сумма полностью. Проанализировать ситуацию.
Решение. Тогда np = 4, pS = 20.
Итак, рисковая премия (РП) равна 20, а параметр потока Пуассона 4. Собранная со всего портфеля рисковая премия:
n×РП = 400×20 = 8000
обеспечивает выплату возмещений, если число страховых случаев не превышает 4-х (m ≤ 4, т.е. m = 0,1,2,3,4). Рассчитаем вероятность выполнения страховщиком своих обязательств в этой ситуации. Эти вероятности либо рассчитываются непосредственно, либо берутся из таблицы распределения Пуассона.
Pr(m) = 0.0183, 0.0733, 0.1465, 0.1954, 0.1954;
а их сумма 0.6289 (около 63%).
Очевидно, это не может устроить ни самого страховщика, ни Страхнадзор. Страховщик может повысить свою надежность с помощью следующих четырех основных рычагов: рисковой надбавки (РН), резерва (Р), перестрахования (П) и прибыли от инвестирования временно свободных средств (И).
Последнее позволяет ему опираться на более высокую процентную ставку и за счет этого либо снизить тариф, либо сначала увеличить резерв, с помощью него повысить свою надежность, и уже в результате этого снизить свой тариф. Однако, в данном примере мы не будем рассматривать такую возможность, т.е. ограничиваемся только первыми тремя рычагами.
Итак, предположим, что страховщик назначил относительную надбавку 25%. Тогда его нетто-премия (НП) составит: 20×1.25 = 25.
А со всего портфеля он соберет: 400×25 = 10000, что позволит ему выплатить 5 возмещений (Pr(m=5)= 0.1563). Следовательно, надежность страховщика повысилась на эту величину и достигла значения: 0.7852 (около 78.5%). Полученный результат еще нельзя считать удовлетворительным, поэтому страховщик хочет еще повысить свою надежность. И, прежде всего, анализирует возможность сделать это за счет рисковой надбавки.
162
Если он сможет назначить (и получить со своих страхователей!) относительную надбавку в 50%, то соберет со всего портфеля 12000, что обеспечит ему надежность:
0.7852 + 0.1042 = 0.8894 (около 89%).
Но надо считаться с реальностью. С одной стороны, страхователи не согласятся столько платить, поэтому они уйдут к другому страховщику, у которого более низкие тарифы. (Например, это может быть более крупная компания; вопрос влияния объема портфеля на размер относительной рисковой надбавки подробно рассмотрен в соответствующем разделе.) А с другой стороны, Страхнадзор не удовлетворен столь низкой надежностью, он требует ее повысить, как минимум, до 94%.
Следовательно, надо накапливать сумму Пуассоновских вероятностей до тех пор, пока это (заданное Страхнадзором) значение не будет впервые превышено. Очередное значение: 0.0595 позволяет повысить надежность до 0.8894 + 0.0595 = 0.9489. Это означает, что страховщик должен обеспечить выплату семи возмещений. Поэтому ему необходим резерв для оплаты двух возмещений, т.е. 4000 у.е.
Если же Страхнадзор потребовал обеспечить надежность 0.99, то процесс накопления вероятностей продолжается.
Следующие значения вероятностей: 0.0298, 0.0132 вместе позволяют повысить надежность еще на 0.0430, т.е. достичь надежности 0.9919. Только теперь требуемый Страхнадзором уровень впервые превзойден, поэтому страховщик должен опираться именно на данную ситуацию.
Итак, страховщик должен обеспечить выполнение своих обязательств, если m = 0,1,2, … , 7,8,9. Из этого он может за счет взносов (НП) выплатить лишь 5 первых возмещений. Предположим, что он может иметь резерв 4000, которого достаточно для выплаты еще двух возмещений (m = 6,7). Здесь следует выразить сомнение, что страховщик (такая сравнительно небольшая компания) может позволить себе иметь резерв, почти равный собираемой суммарной НП. Однако, временно абстрагируемся от этого сомнения. Тогда оставшиеся страховые случаи (m = 8, 9) необходимо передать на перестрахование.
Пример 12. Следовательно, надо найти цену этого перестраховочного договора. Различное число страховых случаев – это несовместные события, поэтому:
2000×(1×0.0298 + 2×0.0132) = 112.4.
Это – рисковая премия за данный перестраховочный договор. Тогда нетто – премия в этом договоре, учитывающая рисковую надбавку перестраховщика (она всегда выше, чем у цедента!), например, 40%, составит: 112.4×1.4 = 157.36, а соответствующая брутто-премия (при нагрузке у перестраховщика: 10% от его тарифа) составит: 187.36/0.9 = 174.8. Это и есть цена данного перестраховочного договора.
163
Если предположить, что страховщик может позволить себе отвлечь в резерв еще 2000 у.е. (для оплаты 8-го страхового случая), то на перестрахование передаются лишь случай № 9. Тогда рисковая премия в таком договоре составит: 2000×1×0.0132 = 26.4 Соответственно, нетто-
премия: 26.4×1.4 = 37, а брутто-премия: 37/0.9 = 41.07.
Следовательно, страховщику надо решить, что для него предпочтительнее: отвлечь дополнительно в резерв 2000, или безвозвратно потерять: 174.8 – 41.1 = 133.7. (около 7% от 2000). Очевидно, его решение будет зависеть от процента, под который можно инвестировать эти 2000 у.е.
Пример 13. Теперь рассмотрим более крупную компанию (n = 2500), работающую с теми же рисками (p = 0.01, S = C = 2000).
Решение. Тогда np = 25 > 20, что позволяет (см. Феллер /27/) использовать нормальную аппроксимацию Пуассоновского распределения:
Pr(X < k |λ) = Ф((k + 0.5 - λ)/  λ ) = Ф((k – 24.5)/5)
λ ) = Ф((k – 24.5)/5)
Для сравнения используем те же значения вероятностей Ф(t):
0.78, 0.89, 0.94, 0.99.
Получим соответствующие значения t: 1.23, 1.55, 1.88, 2.58. Найдем k (с округлением в большую сторону): 31, 33, 34, 38. Собранной суммарной нетто-премии: 25×2500 = 63500 достаточно
для выплаты возмещений по первым 31 случаю (и еще останется 500). Поэтому, если ориентироваться только на резерв, то потребуется соответственно: 3500, 5500, 13500. Наверное, компания может позволить иметь резерв 5500 (8% от собираемой нетто-премии – хорошее соотношение). Возможно, она даже в состоянии обойтись своими средствами, не прибегая к перестрахованию (ведь 13500 составляют всего 21% от собираемой нетто-премии, что вполне приемлемо).
Однако, эти собственные средства компания могла иметь после некоторого периода успешной работы на страховом рынке (например, за счет неиспользованной собранной ранее суммарной рисковой надбавки).
Пример 14. Предположим (для иллюстрации), что страховщик не может себе позволить иметь больший (чем 5500) резерв. Поэтому он вынужден обратиться к перестраховщику. Исследовать ситуацию.
Решение. На перестрахование передаются случаи: 35, 36, 37, 38. Согласно вышеприведенной формуле можно найти вероятности:
Pr(m < 35) = Ф((35 + 0.5 – 25)/5) = Ф(2.1) = 0.9643 (около 96.5%).
Pr(m < 36) = Ф(2.3) |
= 0.9786; |
Pr(m < 37) |
= Ф(2.5) |
= 0.9876; |
|
Pr(m < 38) |
= Ф(2.7) |
= 0.9931; |
Pr(m < 39) |
= Ф(2.9) |
= 0.9963. |
Теперь можно найти вероятности: |
|
|
|
||
Pr(m = 35) |
= 0.9786 |
– 0.9643 = 0.0143; |
|
|
|
Pr(m = 36) |
= 0.9876 |
– 0.9786 = 0.0090; |
|
|
|
164

Pr(m = 37) = 0.9931 – 0.9876 = 0.0055;
Pr(m = 38) = 0.9963 – 0.9931 = 0.0032.
А далее (аналогично предыдущему примеру) можно найти математическое ожидание выплат перестраховщика, (в зависимости от объема переданной ответственности), и определить, тем самым, рисковую премию, а затем нетто-премию и брутто-премию. Сравнив различные варианты, выбираем наиболее приемлемый.
Замечание. Сравнение этих трех примеров показывает принципиальную возможность использования различных методик при исследовании страхового портфеля. Данное соображение и лежит в основе двух основных подходов: индивидуальных и коллективных моделей, которым посвящены соответствующие разделы.
9.4. Закон Пуассона и экспоненциальное распределение. Их использование в страховании.
Для страхования свойственно, что имеется большое число однородных договоров, в каждом из которых вероятность наступления страхового случая мала и одинакова. Поэтому вероятность сложного события, состоящего в том, что число страховых случаев примет фиксированное значение, может быть рассчитана не по точной формуле Бернулли, а по приближенной - формуле Пуассона. Закон Пуассона для распределения количества страховых случаев широко используется в страховании, например, в имущественном.
Pr(m=k) = e-λ λk/ k!
Если число случаев подчинено закону Пуассона с параметром λ, то время между двумя последовательными событиями подчиняется экспоненциальному закону с тем же параметром λ. При этом вероятность того, что время между двумя последовательными событиями не превзойдет «x», определяется по формуле:
F(t<x) = 1 - e-λx (Рис. 9.1.).
Этой интегральной функции соответствует дифференциальная
функция (плотность распределения):
= λ e-λx (Рис. 9.2.).
F(x) |
f(x) |
|
λ |
1/λ |
1/λ |
x |
x |
(Рис. 9.1.) |
(Рис. 9.2.) |
165
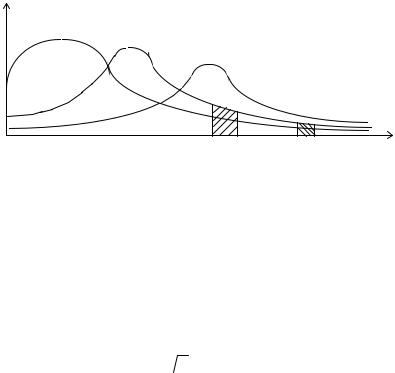
Поскольку площадь под кривой плотности равна 1, то с ростом λ левая граница фигуры поднимается, но кривая убывает более круто. При x→∞ кривая асимптотически приближается к горизонтальной оси. (Рис. 9.3.).
P(m=k)
λ2 (λ1, λ2)
λ1 |
λ3 |
k
Рис. 9.3.
Верно и обратное утверждение, если время между двумя последовательными событиями подчиняется экспоненциальному закону, то число событий за единицу времени подчиняется распределению Пуассона с тем же параметром. С увеличением λ распределение Пуассона приближается к нормальному, что позволяет упрощать расчеты. Феллер утверждает /27/, что при λ > 20 справедлива приближенная формула:
Pr(x< k/λ) = Ф((k+0.5-λ)/  λ )
λ )
Здесь учитывается, что M(k) = D(k) =λ. Это приближение может быть использовано для оценки вероятности разорения, а следовательно и для определения рисковой надбавки.
Оценка параметра λ, полностью определяющего оба интересующих нас распределения, может быть получена с помощью метода максимального правдоподобия.
Закон распределения суммы n независимых случайных величин, имеющих экспоненциальное распределение (с одним и тем же значением параметра), называется законом распределения Эрланга (n-1) порядка. В частном случае при n=1 (n-1=0) получаем распределение Эрланга 0 порядка или экспоненциальное распределение. Для к-го порядка плотность:
Pk(t)=λ e-λt (λt)k/ k!
Видно, что при увеличении интенсивности λ форма кривой плотности распределения Пуассона приближается к нормальной плотности.
При одинаковой длине отрезков нормальная аппроксимация точнее на отрезке, более удаленном от вершины распределения (моды).
В. Феллер /27/ утверждает, что ошибка нормального приближения мала, если n p q велико (это означает, что n p велико). С другой стороны, при больших n и малых p, вероятность биномиального
166

распределения b(k, n, p) хорошо аппроксимируется пуассоновскими вероятностями p(k, λ=n p). При малых λ можно пользоваться только пуассоновскими приближениями, но с ростом λ появляется возможность как пуассоновского, так и нормального приближения. Поэтому возникает возможность нормальной аппроксимации пуассоновского распределения. В частности, используя формулу Стирлинга, можно показать, что для фиксированных α, β при λ→∞:
∑Ρ(k ,λ) → [Φ(β)−Φ(α)] /2 ; λ+α λ < k< λ+β
λ < k< λ+β λ
λ
Из центральной предельной теоремы следует, что если случайные величины Xk подчиняются распределению Пуассона P(k,λ), то
Sn=X1+...+Xn имеет распределение Пуассона P(k, n λ). Поэтому при n→∞: (Pk + …) = Ф(b) при k<λ+b λ0.5. Это утверждение справедливо
при любом характере стремления λ к ∞.
Пусть Sm = X1+...+Xm, m имеет распределение Пуассона. Его математическое ожидание M(m)=λ t. Если все слагаемые подчинены одному и тому же распределению (f(i)), то Sm имеет обобщенное
распределение Пуассона: |
= e−λt ∑∞ [(λt)k /k!]{fi }k |
{hi }t |
|
|
k =0 |
с производящей функцией: |
ht (S) =e−λt+λt f(S) |
Например, если число ударов молнии в любом интервале времени длительности t является пуассоновской случайной величиной с математическим ожиданием λ t, и (f(n)) - распределение вероятностей ущерба, причиненного одним ударом молнии, то при условии стохастической независимости суммарный ущерб за время t имеет обобщенное распределение Пуассона. Очевидно, что вместо удара молнии можно рассматривать страховой случай.
Предположим, что страховщик заключил договор о перестраховании, по которому он отвечает за первый страховой случай, а перестраховщик за второй. Известно, что время ожидания очередного страхового случая распределено по экспоненциальному закону с параметром λ. Перестраховщика интересует момент наступления его ответственности. Найти закон распределения времени до наступления второго случая.
Пусть Y1 - время ожидания первого случая, а Y2 - величина времени от первого до второго случая. Тогда время до второго случая Y=Y1+Y2. По условию Y1 и Y2 подчиняются экспоненциальному закону с плотностью:
0, t < 0 P(t) = λ e−λt , t > 0
167

Из независимости Y1,Y2 плотность распределения Y=Y1+Y2
имеет вид: PY1+Y2 (t) = |
∞∫PY1(x) PY2 (t −x) dx = |
∞∫λ e−λt PY2 (t −x) dx если |
|
−∞ |
0 |
x>t, то t-x <0, следовательно, P (t-x)=0. Тогда
PY1+Y2 (t) = ∫t λe−λx λe−λ(t−x) dx = λ2 e−λt ∫t dx = (λe−λt ) (λt) = PY1 (t) (λt)
0 |
0 |
Использована процедура свертки функций.
При оценке варианта перестрахования обе стороны интересует не столько вероятность попадания на заданный интервал, сколько вызванное этим значение затрат (математическое ожидание выплачиваемых страховых сумм), на основании которого определяется цена перестрахования.
|
β |
Точное значение этой величины равно: |
∑e −λ λk /k! k |
|
α |
А на основании нормальной аппроксимации получим:
β tп
∫x f(x)dx ≈ ∫(λ+  λ t) f(t) dt = λ ∫f(t)dt =λ ∫t f(t) dt = λ P +
λ t) f(t) dt = λ ∫f(t)dt =λ ∫t f(t) dt = λ P +  λ M(t)
λ M(t)
αtо
где f(t) =1/( 2π) e−t t/2 .
2π) e−t t/2 .
Итак:
tп |
|
|
|
∫tet t/2dt = ∫e−t t/2dt 2 /2 = ∫e−u du =− ∫e−u d(−u) = −∫d(e−u ) = |
|||
tо |
|
|
|
tп |
= e− |
t 2 tо |
|
= −e−u |
2 |
tп |
|
tо |
|
|
|
Математическое ожидание: λP +  λ (e−(tл tл )/2 − e−(tп tп )/2 ).
λ (e−(tл tл )/2 − e−(tп tп )/2 ).
Это и будет платой за перестрахование, если передается риск выплаты страхового покрытия для пострадавших клиентов с α до β включительно. Рассмотрим «комплексный пример». Зададим α=16 и β=18. Сравним значение, вычисленное непосредственно (0.692), со значением, рассчитанным с помощью аппроксимации (0.501). Значение параметра λ=10 еще мало и не позволяет получить хорошую аппроксимацию.
Сопоставление передаваемого риска и платы за перестрахование позволяет получить представление о целесообразности передачи перестраховщику риска в любом диапазоне ( α,β).
168
9.5.Использование процедуры свертки в оценке общего ущерба
Рассмотрим применение свертки в актуарных расчетах. Эта необходимость возникает в малых по объему и неоднородных по составу портфелях, когда нормальная аппроксимация еще неприменима.
Пример 15. Портфель из четырех одинаковых договоров, согласно которым возможна (условно) компенсация полного ущерба в 2 е.с.с. с вероятностью 0.1 или частичного ущерба в 1 е.с.с. с вероятностью 0.1. Найти рисковую премию и нетто – премию в этом портфеле.
Решение. С рисковой премией трудностей не возникает. Ожидаемый ущерб равен: 2 0.1 + 1 0.1 + 0 0.8 = 0.3. Следовательно, страховщик соберет суммарную рисковую премию 1.2 , что позволит ему за счет взносов клиентов выплатить возмещение только для одного страхового случая с частичным ущербом.
Для оценки устойчивости этого страховщика следует оценить
распределение суммарного ущерба по всем четырем договорам.
Есть 4 независимые одинаково распределенные случайные величины. При анализе будем последовательно переходить от одной величины к двум, затем от двух к трем, и т.д. Итак, для двух величин возможны 9 различных вариантов:
|
X1 = 0 |
X1 = 1 |
X1 = 2 |
X2 = 0 |
0.64 |
0.08 |
0.08 |
X2 = 1 |
0.08 |
0.01 |
0.01 |
X2 = 2 |
0.08 |
0.01 |
0.01 |
Преобразуем эту таблицу в таблицу распределения новой случайной величины: X1 + X2 .
X1+X2 |
0 |
1 |
2 |
3 |
4 |
P |
0.64 |
0.16 |
0.17 |
0.02 |
0.01 |
Теперь построим новую таблицу, добавив величину X3.
P3/P(1+2) |
0.64 |
0.16 |
0.17 |
0.02 |
0.01 |
0.8 |
0.512 |
0.128 |
0.136 |
0.016 |
0.008 |
0.1 |
0.064 |
0.016 |
0.017 |
0.002 |
0.001 |
0.1 |
0.064 |
0.016 |
0.017 |
0.002 |
0.001 |
Поэтому для распределения X1 + X2 + X3 имеем таблицу:
(k) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
P(k) |
0.512 |
0.192 |
0.216 |
0.049 |
0.027 |
0.003 |
0.001 |
169
Аналогично построим матрицу для присоединения X4.
0.4096 |
0.1536 |
0.1728 |
0.0392 |
0.0216 |
0.0024 |
0.0008 |
0.0512 |
0.0192 |
0.0216 |
0.0049 |
0.0027 |
0.0003 |
0.0001 |
0.0152 |
0.0192 |
0.0216 |
0.0049 |
0.0027 |
0.0003 |
0.0001 |
Тогда распределение X1 + X2 |
+ X3 + X4 имеет вид: |
|
||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
.4096 |
.2048 |
.2432 |
.0800 |
.0481 |
.0100 |
.0038 |
.0004 |
.0001 |
Накопленная вероятность соответственно равна: |
|
|||||||
.4096 |
.6144 |
.8576 |
.9376 |
.9857 |
.9957 |
.9995 |
.9999 |
1.0 |
Отсюда видно, что при собранной суммарной рисковой премии 1.2 вероятность неразорения составит всего 0.6144 (менее 62%), что недопустимо мало. Следовательно, необходимо включить в премию еще и рисковую надбавку. Если страховщик соберет суммарные взносы в размере 3 е.с.с., то он обеспечит вероятность неразорения около 94%, что вполне приемлемо. Отметим, что если страховщик будет ориентироваться на вероятность и захочет обеспечить вероятность неразорения не ниже 90% , то ему потребуется собрать те же 3 е.с.с. Этот результат означает, что премия должна составлять не 0.3 е.с.с., а 3/4 = 0.75 е.с.с., что недопустимо много. Клиент не согласится столько платить. (Нет смысла страховаться!)
Если клиент согласен платить не 0.3, а 0.5, то собранные премии позволяют обеспечить надежность более 85%, что уже близко к норме. Здесь рисковая надбавка составляет 2/3 от рисковой премии. Многовато! Это – следствие малого портфеля и довольно высокой вероятности.
Отметим, что этот же результат может быть получен с помощью другого аппарата, основанного на производящих функциях.
∞
f(z) = ∑Zn P(n)
0
Совпадение производящих функций двух случайных величин означает совпадение распределений этих величин. Это следует из разложения в ряд Тейлора:
f(z) = ∑ Zn f(n) (0) / n! , P(n) = коэффициент при Zn .
Математическое ожидание и дисперсия случайной величины n с производящей функцией f(z) выражаются через производные этой
производящей функции в точке 1. : f′(1) = M(n), f′′(1) = M[n2 ]− M[n];
D[n]= f ′′(1) + f ′(1) − [f ′(1)]2 .
170
