3.2. Графоаналитический метод анализа
Исходные данные:
1=0,5236(30) – угол поворота начального звена;
=33,5
– передаточное отношение многозвенной
зубчатой передачи;
=1650
об/мин – частота вращения электродвигателя.
Описание метода
Графоаналитическое исследование перемещений, скоростей и ускорений ведется для ряда положений механизма, достаточно близко отстоящих друг от друга. В нашем случае механизм изображаем в 12 положениях. Строятся эти положения в результате деления одного оборота главного звена на 12 равных частей, что показано на чертеже (лист №1). Построение ведется в заданном масштабе.
,
где
- угловая скорость начального звена;
-
частота вращения начального звена.
.
Полученные показания перемещения, снятые с чертежа и умноженные на соответствующий масштаб, заносим во второй столбец. В третьем и четвертом столбце вводим формулы соответственно для вычисления скорости и ускорения. Эти формулы основаны на дифференцировании перемещения по времени:
;
.
По полученной таблице строим диаграммы зависимостей Sв(t); Vв(t); aв(t).
Все измерения и полученные результаты сводятся в таблицу 3. А диаграммы зависимостей перемещения, скорости и ускорения точки В от времени показаны на рис. 2,3,4. Аналогичные диаграммы построены на листе №1.
Таблица 3. Результат графоаналитического метода анализа
-
Положение механизма
Перемещение S ,[
]Время t,[
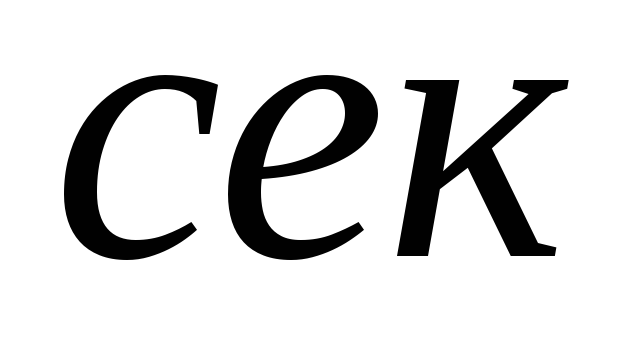]Скорость V,[
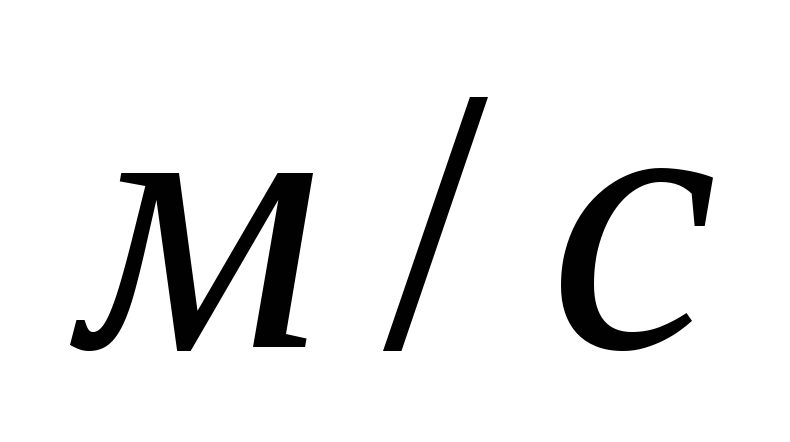]Ускорение а [
]0
0
0
0
22,839
1
0,0346
0,102
0,339
3,328
2
0,114
0,204
0,779
4,309
3
0,217
0,306
1,012
2,282
4
0,331
0,408
1,115
1,008
5
0,444
0,51
1,106
-0,085
6
0,544
0,612
0,985
-1,189
7
0,618
0,714
0,727
-2,525
8
0,644
0,816
0,249
-4,684
9
0,56
0,918
-0,822
-10,499
10
0,297
1,02
-2,577
-17,211
11
0,0576
1,122
-2,329
2,426
12
0
1,224
0
22,839
3.3. Аналитический метод анализа
Описание метода
Вычисление передаточных функций положений, скорости и ускорений точек звеньев с использованием ЭВМ проводят по соответствующим формулам. Эти формулы выводятся после анализа и нахождения зависимостей определенных элементов кинематической схемы от изменяющегося параметра, закон изменения которого заранее известен. Этих параметров может быть несколько. В нашем случае один параметр – 1 – угол поворота начального звена O2A.
Получение аналитических зависимостей
Все
необходимые схемы для анализа 
показано
на рис. 5
Скорость точки A:
,
(1)
где
– скорость точкиO2;
– скорость звенаO2A.
Скорость точки O3
,
(2)
где
;
– скорость точки
A
относительно звена BO3;
– скорость звена
AO3.
Принимаем
т. A
за начало координат, векторы 
и 
за оси x1,
y1.
Проецируем
на оси координат:
Очевидно
что:
,
Рис.2
где
О2
А VA)
=(180˚ - (φ2
+ (90˚- φ1))
- 90˚ = φ1
- φ2
VAO3 = VA sin(φ1 - φ2 ) VABO3 = VA cos (φ1 – φ2 )
Также VAO3 можно найти через ω2 :
VAO3 = ω2 O3A => ω2 = VAO3 /O3A = VA sin (φ1 – φ2)/O3A
Учитывая формулу (1) ω2 = ω1 O2A sin(φ1 – φ2)/O3A
По теореме косинусов из треугольника O2AO3 находим
O3A
=
Можно
записать, учитывая, что
O3A
=
Выразим φ2 через φ1
φ2
= arctan
φ1
=
VB = VO3 + VBO3, ,
где VO3 =0 – скорость точки O3
VB = VBO3 = ω2 O3N
где O3N = O3B cos(φ2)
Ускорение:
aA = aO2 + a nAO2 + a τAO2
aO2 = 0 –ускорение точки О2
a τAO2 = 0 –тангенциальное ускорение точки А относительно стойки О2
aA = a nAO2 = ω12 O2A
aо3=aa+( a nAO3+ a nAO3B)+(a τAO3+a kA)
Выбираем систему координат аналогично скоростям: т. А начало координат, оси координат вектора ( a nAO3+ a nAO3B),
(a τAO3+a kA)
Ах1=aA*cosα
(a τAO3-a kA)= aA*cosα
a τAO3= aA*cosα+ a kA
кориолисово ускорение:
a kA=2ω2·VABO3
тангенциальное ускорение:
a τAO3=ε2·O3A
ε2=(ω12· O2A·cosα+2ω2·VABO3)/ O3A
aB=aO3+ a nBO3+ a τBO3
ac=aBx= a τBO3· cosφ2+a nBO3· sinφ2
ac= ε2·O3B·cosφ2+ω22·O3B·sinφ2